密码学承诺原理与应用 - 概览
前言
作者:@warm3snow https://github.com/warm3snow
微信公众号:密码应用技术实战
博客园首页:https://www.cnblogs.com/informatics/
简介
承诺方案(Commitment Scheme)是一个重要的密码学原语(cryptographic primitive), 承诺方案是一种加密协议,允许发送者承诺一个选择的值(或声明),同时对接收者保持隐藏,而接收者能够在稍后验证所承诺的值。承诺方案通常可以分为两个阶段。
- 承诺阶段(Commitment Phase): 发送方发送一个承诺值给接收方,这个值是发送方选择的,接收方无法知道这个值的内容。
- 打开阶段(Opening Phase): 发送方打开这个承诺,接收方可以验证这个值的内容。
密码学承诺方案在多个领域有广泛的应用,以下是一些主要的应用场景:
- 电子投票:在电子投票系统中,承诺方案可以确保选民在投票时能够保密其选择,同时在投票结束后能够验证其投票的有效性。
- 拍卖:在拍卖中,承诺方案可以让竞标者在拍卖开始时提交他们的出价,而不透露具体的出价金额。拍卖结束时,所有出价可以被揭示并验证,以确保竞标者的出价是诚实的。
- 安全多方计算:在多方计算中,参与者可以使用承诺方案来承诺他们的输入,而不需要在计算过程中透露这些输入。这有助于保护参与者的隐私。
- 数字签名:承诺方案可以用于构建数字签名方案,确保消息的完整性和不可否认性。
- 区块链和加密货币:在区块链技术中,承诺方案可以用于确保交易的隐私和安全性。例如,某些隐私币(如Zcash)使用承诺方案来隐藏交易金额和发送者信息。
- 身份验证:承诺方案可以用于身份验证协议中,允许用户在不透露其身份信息的情况下证明其身份。
- 游戏理论:在博弈论中,承诺方案可以用于设计机制,使参与者能够在不透露其策略的情况下进行合作或竞争。
承诺方案原理
符号定义
- \(C\): 承诺值
- \(m\): 明文
- \(r\): 随机数,需要保证每次承诺的随机数不同
- \(H\): 哈希函数
- \(||\): 字符串连接
- \([m]\): 明文\(m\)的承诺值
- \([m;r]\): 明文\(m\)和随机数\(r\)的承诺值
- \(G_p\): 模素数\(p\)的阶为\(q\)的循环群
- \(g\): \(G_p\)的生成元
- \(h\): \(G_p\)的生成元, 与\(g\)为独立生成元,即g和h生成的子群相互独立
- \(G\): 椭圆曲线上的点,即\((G_x, G_y)\), 通常情况下\(G\)是椭圆曲线的生成元
- \(H\): 椭圆曲线上的点,即\((H_x, H_y)\), 通常境况下\(H\)随机选取
- 明文\(m\)的Pedersen承诺值:\([m;r] = g^m \cdot h^r\)
方案定义
承诺方案是一个三元组, 包含\((Commit, Open, Verify)\),其中:
- \(Commit\):发送方的承诺算法,通常发送方选择一个明文\(m\)和一个随机数\(r\),计算承诺值\(C\)。
- \(Open\):发送方的打开算法, 通常发送方揭示明文\(m\)和随机数\(r\)。
- \(Verify\):接收方的验证算法, 通常接收方验证承诺的正确性。
承诺值有两个属性:
- 隐藏性(Hiding):接收方无法知道发送方的承诺值对应的明文。
- 绑定性(Binding):发送方无法修改承诺值对应的明文。
注:以上两种描述并不严谨
承诺方案一般涉及到两方,发送方和接收方。发送方选择一个明文\(m\)和一个随机数\(r\),计算承诺值\(C\),并发送\(C\)给接收方。在某个时刻,发送方打开承诺,揭示\(m\)和\(r\)。接收方使用\(C\)和揭示的\(m\)和\(r\)验证承诺的正确性。
常见承诺方案和原理
常见的承诺方案有 哈希承诺、ElGamal承诺、Pedersen承诺和 Sigma承诺等。虽然承诺方案的实现方式不同,但其基本原理相似。
关键流程如下:
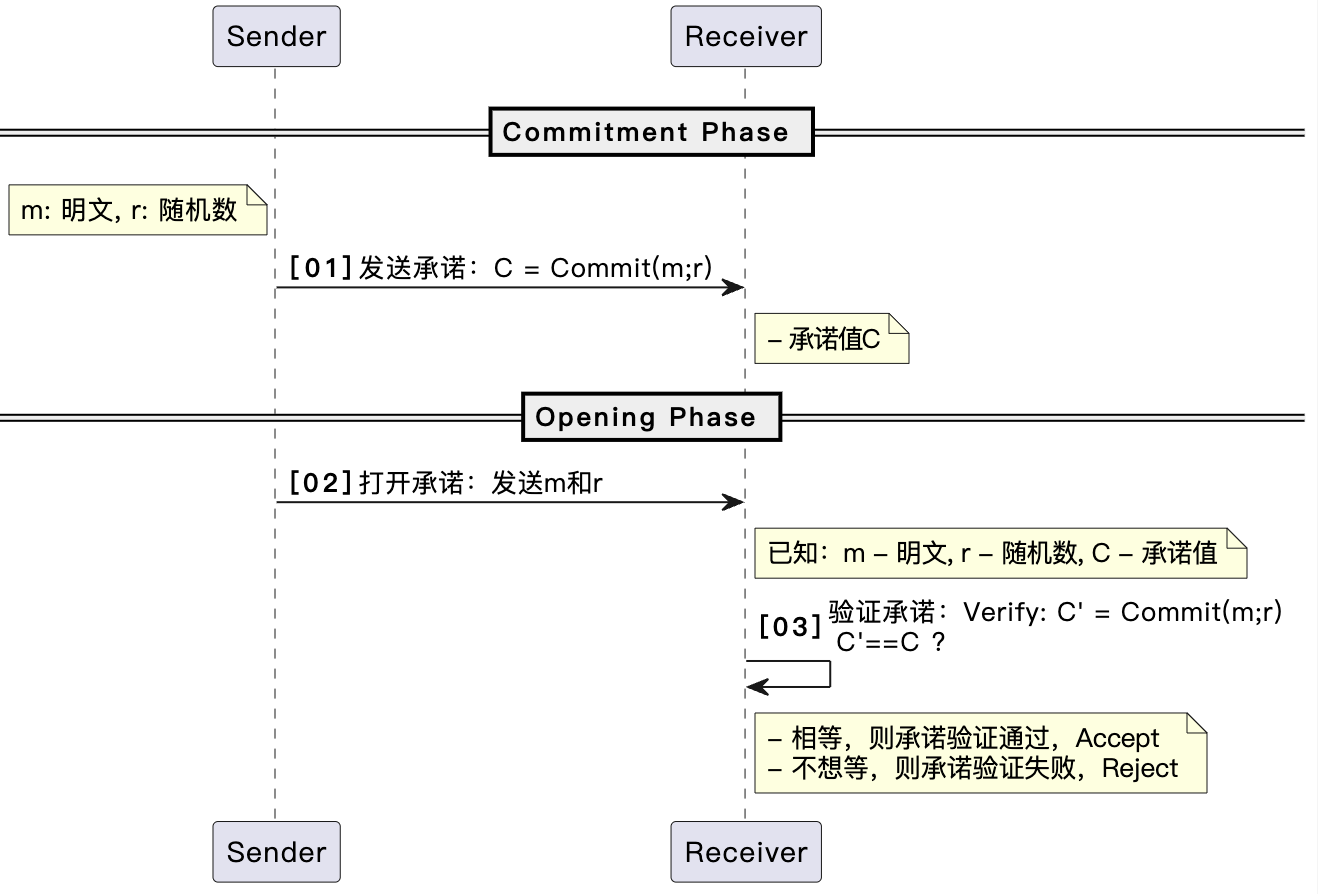
[01] 发送承诺:Sender选取随机数\(r\), 并计算\(m\)的承诺值\(C\),发送给Receiver。(这里的随机数\(r\)是为了保证每次承诺的值不同)
[02] 打开承诺:Sender打开承诺,揭示\(m\)和\(r\)。
[03] 验证承诺:Receiver重新计算承诺值\(C^{'}\),并验证\(C^{'}\)和\(C\)是否相等。相等则认为承诺验证通过,否则承诺验证失败。
哈希承诺
哈希承诺是一种简单的承诺方案,通过哈希函数来实现承诺。假设\(H\)是一个哈希函数,\(m\)是明文。
哈希承诺的构造如下:
- 承诺阶段:发送方选择一个明文\(m\),计算承诺值\(C = H(m)\),并发送\(C\)给接收方。
- 打开阶段:发送方揭示明文\(m\)。
- 验证阶段:接收方重新计算承诺值\(C^{'} = H(m)\),并验证\(C^{'}\)和\(C\)是否相等。
哈希承诺的隐藏性和绑定性是基于哈希函数的性质,哈希函数是单向函数,接收方无法从承诺值\(C\)推导出明文\(m\)。同时,哈希函数是抗碰撞的,发送方无法找到两个不同的\(m\),使得\(C = H(m)\)。
哈希承诺隐藏性较差,在明文空间有限的情况下,可能会发生碰撞; 哈希承诺对于相同的明文\(m\),承诺值\(C\)是固定的,虽然引入随机数\(r\)可以解决这个问题,但会破坏绑定性,因为发送方可以在保证\(m||r\)不变的情况下,随便更改\(m\)和\(r\)的值。
ElGamal承诺
ElGamal承诺是一种基于离散对数问题的困难性假设构造的承诺方案。假设\(G_p\)是阶为\(q\)的循环群,\(g, h\)是生成元, \(m\)是明文
ElGamal承诺的构造如下:
- 承诺阶段:发送方选择一个明文\(m\)和一个随机数\(r\),计算承诺值\(C = (g^r, m \cdot h^r)\),并发送\(C\)给接收方。
- 打开阶段:发送方揭示明文\(m\)和随机数\(r\)。
- 验证阶段:接收方重新计算承诺值\(C^{'} = (g^r, m \cdot h^r)\),并验证\(C^{'}\)和\(C\)是否相等。
ElGamal承诺的隐藏性和绑定性是基于离散对数问题的困难性假设,接收方无法从承诺值\(C\)推导出明文\(m\),发送方无法找到两个不同的\((r_1, m_1)\)和\((r_2, m_2)\),使得\(C = (g^{r_1}, m_1 \cdot h^{r_1}) = (g^{r_2}, m_2 \cdot h^{r_2})\)。
假设发送方找到两个不同的\((r_1, m_1)\)和\((r_2, m_2)\),使得\(C = (g^{r_1}, m_1 \cdot h^{r_1}) = (g^{r_2}, m_2 \cdot h^{r_2})\),则有:
与假设矛盾,因此ElGamal承诺具有绑定性。
Pedersen承诺
Pedersen承诺是一种基于离散对数问题的困难性假设构造的承诺方案。假设\(G_p\)是阶为\(q\)的乘法群,\(g, h\)是独立生成元,\(m\)是明文。
Pedersen承诺的构造如下:
- 承诺阶段:发送方选择一个明文\(m\)和一个随机数\(r\),计算承诺值\(C = g^m \cdot h^r\),并发送\(C\)给接收方。
- 打开阶段:发送方揭示明文\(m\)和随机数\(r\)。
- 验证阶段:接收方重新计算承诺值\(C^{'} = g^m \cdot h^r\),并验证\(C^{'}\)和\(C\)是否相等。
Pedersen承诺的隐藏性和绑定性是基于离散对数问题的困难性假设,接收方无法从承诺值\(C\)推导出明文\(m\),发送方无法找到两个不同的\((r_1, m_1)\)和\((r_2, m_2)\),使得\(C = g^{m_1} \cdot h^{r_1} = g^{m_2} \cdot h^{r_2}\)。
假设发送方找到两个不同的\((r_1, m_1)\)和\((r_2, m_2)\),使得\(C = g^{m_1} \cdot h^{r_1} = g^{m_2} \cdot h^{r_2}\),则有:
由于\(g\)和\(h\)是独立生成元, 即它们生成的子群没有重叠,这意味着\(g^{m_1 - m_2} = h^{r_2 - r_1}\)只有在\(_1 - m_2 = 0\)和\(r_2 - r_1 = 0\)时才成立,即:
与假设矛盾,因此Pedersen承诺具有绑定性。
Pedersen承诺也可以基于ECC构造,假设\(G\)和\(H\)是椭圆曲线上的点,\(m\)是明文,\(r\)是随机数。
- 承诺阶段:发送方选择一个明文\(m\)和一个随机数\(r\),计算承诺值\(C = mG + rH\),并发送\(C\)给接收方。
- 打开阶段:发送方揭示明文\(m\)和随机数\(r\)。
- 验证阶段:接收方重新计算承诺值\(C^{'} = mG + rH\),并验证\(C^{'}\)和\(C\)是否相等。
隐藏性和绑定性略,与上述类似。
Pedersen承诺有一个重要的性质:同态性。即两个Pedersen承诺的和等于明文的和的Pedersen承诺。假设\(C_1 = g^{m_1} \cdot h^{r_1}\)和\(C_2 = g^{m_2} \cdot h^{r_2}\)是两个Pedersen承诺,\(m_1, m_2\)是明文,\(r_1, r_2\)是随机数。则有:
使用ECC构造的Pedersen承诺也具有同样的性质。如下:
Pedersen承诺的同态性可以用于保证密态的加法性,即两个密文的和等于明文的和的密文。如在门罗币中,矿工节点通过验证Pedersen承诺可以检查交易UTXO的输入和是否等于输出和(是否凭空产生门罗币)。
零知识证明承诺
在上一章中介绍的承诺方案中,发送方和接收方之间的通信是明文的,即接收方可以获得发送方的明文信息。在某些情况下,发送方希望向接收方证明自己拥有某个明文,而不透露明文的具体内容。这时,可以使用 零知识证明承诺方案。
零知识证明承诺是一种特殊的承诺方案,允许发送方向接收方证明自己拥有某个明文,而不透露明文的具体内容。零知识证明承诺方案根据在证明阶段是否交互可以分为:
- 交互式零知识证明承诺:发送方和接收方之间需要交互,发送方向接收方发送证明,接收方验证证明。
- 非交互式零知识证明承诺:发送方可以在不与接收方交互的情况下生成证明,接收方可以验证证明。
Sigma承诺
Sigma承诺是一种基于离散对数问题的困难性假设构造的零知识承诺方案。Sigma承诺的交互式证明流程如下:
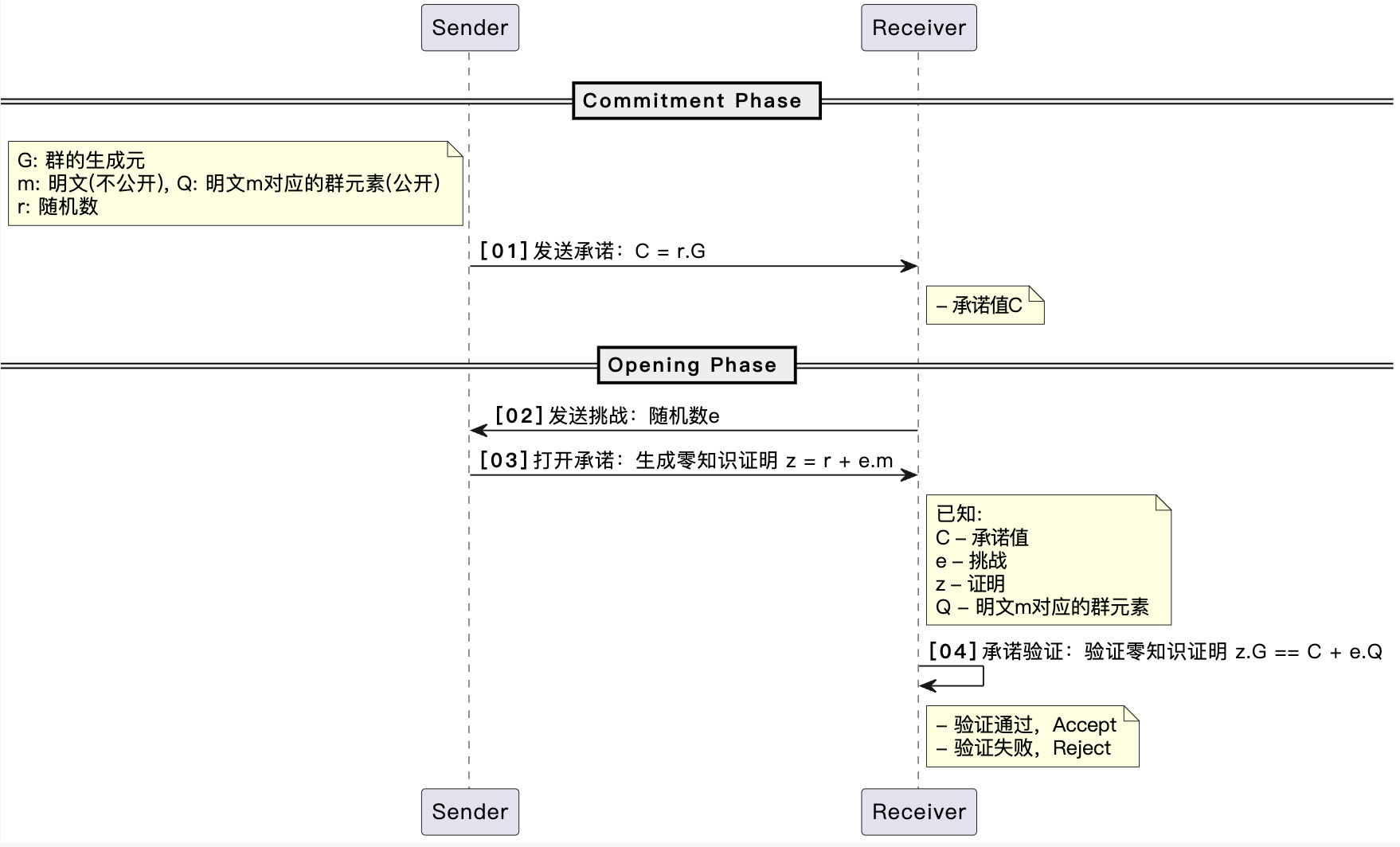
- [01] 发送承诺:Sender选取随机数\(r\),并生成承诺\(C = r.G\),发送\(C\)给Receiver。
- [02] 发送挑战:Receiver发送一个随机挑战\(e\)给Sender;
- [03] 发送挑战:Sender计算证明\(z = m + er\),并发送给Receiver。(注这里的proof是z,用于隐藏r和m)
- [04] 承诺验证:Receiver验证Proof, 即验证\(z.G == C + e.Q\)。
Sigma承诺正确性证明
等式左边等于等式右边,因此按照Sigma承诺协议流程,验证方Receiver可以正确验证
Sigma承诺隐藏性证明
非严格证明,由于Receiver仅知道\(C\),根据离散对数问题的困难性假设,Receiver无法计算出\(r\)的值,保证了承诺的隐藏性。
Sigma承诺绑定性证明
假设Receiver可以找到两个不同的\((r_1)\)和\((r_2)\),使得\(C = r_1.G = r_2.G\),则有:
与假设矛盾,因此Sigma承诺具有绑定性。
Sigma承诺零知识性证明
非严格证明,由于Receiver仅知道\((Q, C, e, z)\),并且基于该已知信息,无法计算出\(m\)的值,保证了承诺的零知识性
Sigma非交互式零知识证明承诺
Sigma承诺也可以使用Fiat-Shamir heuristic构造为非交互式零知识证明承诺。具体流程如下:
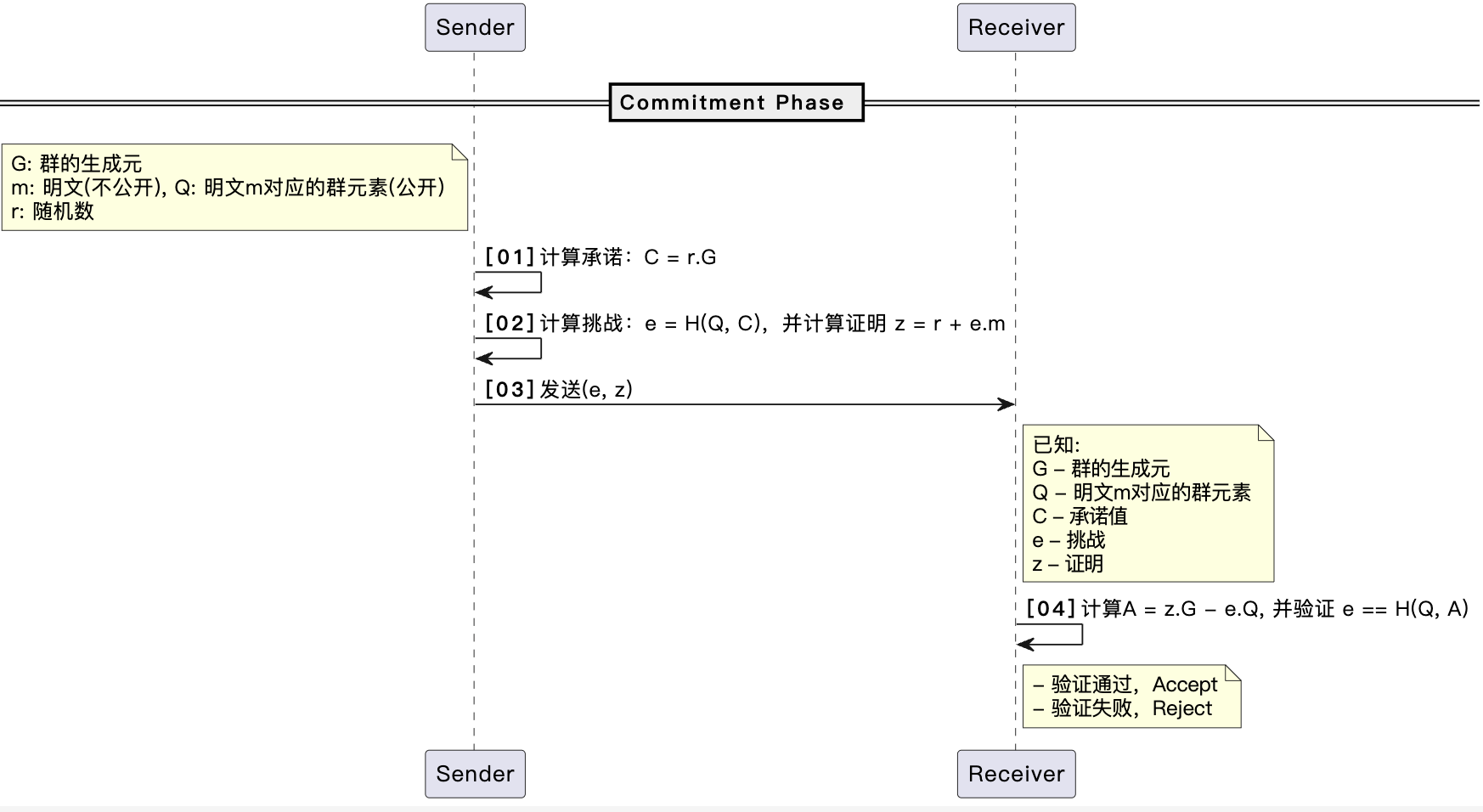
- [01] 计算承诺:Sender选取随机数\(r\),并生成承诺\(C = r.G\);
- [02] 计算挑战:Sender计算挑战\(e = H(Q, C)\),并计算证明\(z = r + e.m\);
- [03] 发送(e, z):Sender发送挑战\(e\)和证明\(z\)给Receiver;
- [04] 验证:Receiver计算\(A = z.G - e.Q\),并验证\(e == H(Q, A)\)。
Sigma承诺的非交互式零知识证明承诺的正确性、隐藏性、绑定性和零知识性证明与交互式零知识证明承诺类似。需要注意的是:
- 非交互式零知识证明承诺的安全性与哈希函数的选择有关,需要选择一个安全的哈希函数。
- 与交互式零知识证明承诺相比,非交互式零知识证明承诺的性能更好,因为发送方和接收方之间不需要交互。
- 与交互式零知识证明承诺相比,非交互式零知识证明承诺发送的数据量更小,数据量只有挑战\(e\)和证明\(z\),不需要发送承诺值\(C\)。
Pedersen零知识承诺
Pedersen承诺也可以构造为零知识承诺方案。 下面我们直接介绍非交互式版本的Pedersen零知识承诺方案。
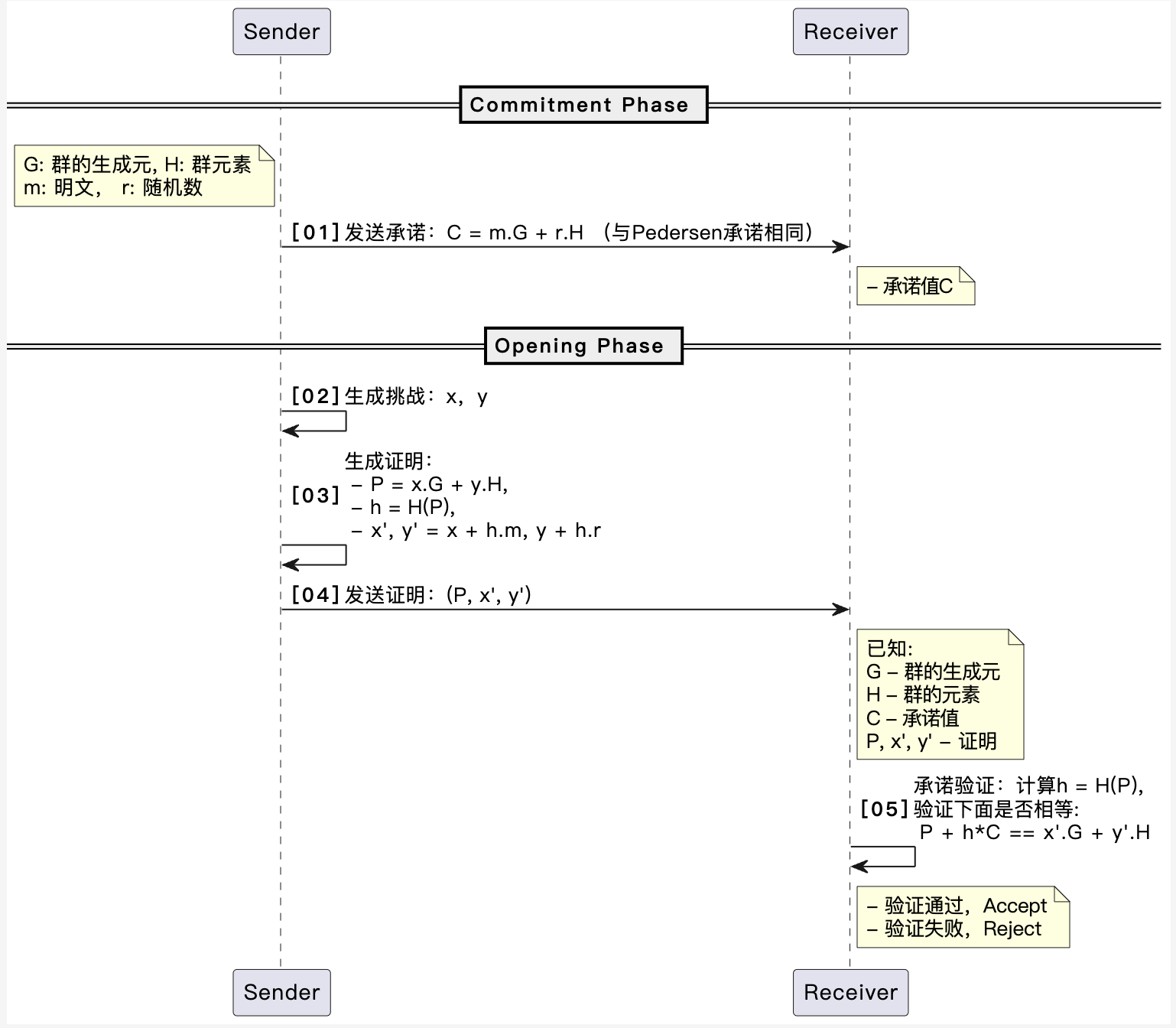
- [01] 发送承诺:Sender选取随机数\(r\),并生成承诺\(C = m.G + r.H\),发送\(C\)给Receiver。(承诺阶段不变)
- [02] 生成挑战:Sender生成两个随机数\(x\)和\(y\);
- [03] 生成证明:Sender计算\(P = x.G + y.H\),并计算\(h = H(P)\),然后计算\(x^{'} = x + h.m\)和\(y^{'} = y + h.r\);
- [04] 发送证明:Sender发送证明\((P, x^{'}, y^{'})\)给Receiver;
- [05] 验证:Receiver验证证明,计算\(h = H(P)\),并验证\(P + h.C == x^{'}G + y^{'}H\)。
Pedersen零知识承诺的隐藏性、绑定性与Pedersen承诺类似。需要注意的是:
- Pedersen零知识承诺的安全性与哈希函数的选择有关,需要选择一个安全的哈希函数。
Pedersen零知识承诺的正确性证明
等式左边等于等式右边,因此按照Pedersen零知识承诺协议流程,验证方Receiver可以正确验证.
Pedersen零知识承诺的零知识性证明
非严格证明,由于Receiver仅知道\((C, P, x^{'}, y^{'})\),并且基于该已知信息,无法计算出\(m\)和\(r\)的值,保证了承诺的零知识性。
承诺方案对比
下表对比了哈希承诺、ElGamal承诺、Pedersen承诺和Sigma承诺的性质:
| 承诺方案 | 隐藏性 | 绑定性 | 同态性 | 零知识性 | 性能 | |
|---|---|---|---|---|---|
| 哈希承诺 | 差 | 差 | 否 | 否 | 高 |
| ElGamal承诺 | 好 | 好 | 是 | 否 | 较高 |
| Pedersen承诺 | 好 | 好 | 是 | 否 | 较高 |
| Sigma承诺-交互式 | 好 | 好 | 是 | 是 | 一般 |
| Sigma承诺-非交互式 | 好 | 好 | 是 | 是 | 较高 |
| Pedersen零知识承诺-非交互式 | 好 | 好 | 是 | 是 | 较高 |
通过对比发现,Pedersen承诺和Sigma承诺是比较优秀的承诺方案,具有隐藏性、绑定性和同态性。Sigma承诺是一种零知识承诺方案,可以保证发送方向接收方证明自己拥有某个明文,而不透露明文的具体内容。Pedersen承诺具有同态性,可以用于保证密文的加法性。因此,Pedersen承诺和Sigma承诺在实际应用中具有广泛的应用。
总结
本文介绍了承诺方案的基本原理和常见的承诺方案,包括哈希承诺、ElGamal承诺、Pedersen承诺和Sigma承诺。承诺方案是一种重要的密码学原语,可以用于保证发送方的承诺值对应的明文,同时隐藏明文的具体内容。承诺方案在多个领域有广泛的应用,包括电子投票、拍卖、安全多方计算、数字签名、区块链和加密货币、身份验证和游戏理论等。通过对比发现,Pedersen承诺和Sigma承诺是比较优秀的承诺方案,具有隐藏性、绑定性和同态性。Pedersen承诺具有同态性,可以用于保证密文的加法性。Sigma承诺是一种零知识承诺方案,可以保证发送方向接收方证明自己拥有某个明文,而不透露明文的具体内容。因此,Pedersen承诺和Sigma承诺在实际应用中具有广泛的应用。
希望通过本文的介绍,读者对承诺方案有一个更深入的了解,为实际应用提供参考。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号