信息安全数学基础的几个C语言代码
相关书籍：《信息安全数学基础-陈恭亮-清华大学出版社-第2版》 (豆瓣)
1.埃氏筛
/*输入一个正整数，输出小于其的全部素数*/
#include <stdio.h>
#include <stdbool.h>
#define MAXN 100001
bool vis[MAXN]={1,1};
void Era(int qwq){
for(int i=2;i<=qwq;i++){
if(vis[i]){
continue;
}
for(int j=i*2;j<=qwq;j+=i){
vis[j]=true;
}
}
}
int main(){
int n;
scanf("%d", &n);
Era(n);
for(int i=2;i<=n;i++){
if(!vis[i]){
printf("%d ", i);
}
}
return 0;
}
2.1欧几里得算法递归形式
/*输入两个整数，输出二者的最大公约数*/
#include <stdio.h>
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
int main(){
int m,n,ans;
scanf("%d %d",&m, &n);
ans=gcd(m,n);
printf("%d", ans);
return 0;
}
2.2欧几里得算法迭代形式
/*输入两个整数，输出二者的最大公约数*/
#include <stdio.h>
int gcd(int a,int b){
int t;
while(b){
t=a%b;
a=b;
b=t;
}
return a;
}
int main(){
int m,n,ans;
scanf("%d %d",&m, &n);
ans=gcd(m,n);
printf("%d", ans);
return 0;
}
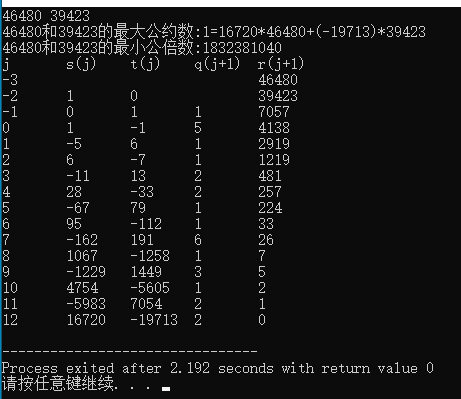
3.广义欧几里得除法及最小公倍数
/*输入两个整数，求出二者的最大公约数和最小公倍数，并将求gcd的过程打表*/
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
long long tab[MAXN][4]={0};
// 交换函数，保证a >= b
void order(int *a, int *b) {
if (*a < *b) {
int t = *a;
*a = *b;
*b = t;
}
}
int main() {
int m, n, step, s, t, gcd;
scanf("%d %d", &m, &n);
order(&m, &n);
tab[0][3] = m, tab[1][3] = n;
tab[1][0] = 1, tab[1][1] = 0;
if (n == 0) {
step = 1, s = 1, t = 0, gcd = m;
} else {
for (int i = 2;; i++) {
tab[i][2] = tab[i - 2][3] / tab[i - 1][3];
tab[i][3] = tab[i - 2][3] % tab[i - 1][3];
if (i == 2) {
tab[2][0] = 0, tab[2][1] = 1;
} else {
tab[i][0] = tab[i - 2][0] - tab[i - 1][0] * tab[i - 1][2];
tab[i][1] = tab[i - 2][1] - tab[i - 1][1] * tab[i - 1][2];
}
if (tab[i][3] == 0) {
step = i;
s = tab[i][0], t = tab[i][1], gcd = tab[i - 1][3];
break;
}
}
}
printf("%d和%d的最大公约数:%d", m, n, gcd);
if(s>=0&&t>=0){
printf("=%d*%d+%d*%d\n",s,m,t,n);
}
else if(s>=0&&t<0){
printf("=%d*%d+(%d)*%d\n",s,m,t,n);
}
else if(s<0&&t>=0){
printf("=(%d)*%d+%d*%d\n",s,m,t,n);
}
else if(s<0&&t<0){
printf("=(%d)*%d+(%d)*%d\n",s,m,t,n);
}
printf("%d和%d的最小公倍数:%d\n",m,n,m/gcd*n);
printf("j s(j) t(j) q(j+1) r(j+1)\n");
for (int i = 0; i <= step; i++) {
if (i == 0) {
printf("%-8d\t\t\t%-8lld\n", i - 3, tab[i][3]);
} else if (i == 1) {
printf("%-8d%-8lld%-8lld\t%-8lld\n", i - 3, tab[i][0], tab[i][1], tab[i][3]);
} else {
printf("%-8d%-8lld%-8lld%-8lld%-8lld\n", i - 3, tab[i][0], tab[i][1], tab[i][2], tab[i][3]);
}
}
return 0;
}
4.定理1.1.9算法
/*编程实现欧几里得除法(定理1.1.9)并可判断整数a是否被非零整数b整除*/
#include <stdio.h>
int main(){
int a,b;
scanf("%d %d", &a, &b);
printf("%d=%d*%d+%d\n",a,a/b,b,a%b);
if(a%b==0){
printf("%d能被%d整除\n",a,b);
}
else{
printf("%d不能被%d整除\n",a,b);
}
return 0;
}
5.定理1.5.1算法
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define ll long long
ll gcd(ll a, ll b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
int main() {
ll n, s, t, p1, p2, a, b, end = 0;
scanf("%lld", &n);
for (ll i = n; i > 0; i += n) {
for (ll j = 2; j <= sqrt(i); j++) {
if (i % j == 0) {
s = j;
t = i / j;
if (n % s && n % t) {
p1 = gcd(n, s);
p2 = gcd(n, t);
if (p1 != 1 && p1 != n && p2 != 1 && p2 != n) {
a = (t + s) / 2;
b = (t - s) / 2;
printf("a=%lld, b=%lld, a-b=%lld, a+b=%lld\n", a, b, s, t);
printf("(%lld,%lld)=%lld和(%lld,%lld)=%lld都是%lld的真因数\n", n, s, p1, n, t, p2, n);
end = 1;
break;
}
}
}
}
if (end) break;
}
return 0;
}
6.定理1.6.4算法
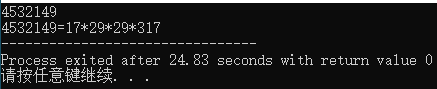
/*编程实现整数的素因数分解(定理1.6.4)*/
#include <stdio.h>
#include <stdlib.h>
#define MAXN 1000
int main(){
int a[MAXN],n,q=0;
scanf("%d", &n);
printf("%d=",n);
for(int i=2;i<=n;i++){
while(n%i==0){
a[q++]=i;
n/=i;
}
}
for(int i=0;i<q;i++){
if(i==0) printf("%d",a[i]);
else printf("*%d",a[i]);
}
return 0;
} 
7.定理2.3.3
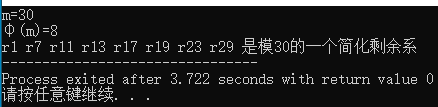
/*输入m和φ(m),输出模m的一个简化剩余系(定理2.3.3)*/
#include <stdio.h>
#define MAXN 10000
int gcd(int a,int b){
int t;
while(b){
t=a%b;
a=b;
b=t;
}
return a;
}
int main(){
int m,n,a[MAXN],cnt=0;
printf("m=");
scanf("%d", &m);
printf("φ(m)=");
scanf("%d", &n);
for(int i=1;i<m;i++){
if(gcd(i,m)==1) a[cnt++]=i;
}
for(int i=0;i<n;i++){
printf("r%d ",a[i]);
}
printf("是模%d的一个简化剩余系",m);
return 0;
}
8.计算同余式ax≡b(modm)
/*计算同余式ax≡b(modm)*/
#include <stdio.h>
int exgcd(int a,int b,int *x,int *y) { //ax+by=gcd(a,b)=d
if (!b) {
*x=1, *y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
*y-=a/b* *x;
return d;
}
int main() {
int a,b,m,s,t,d,k;
scanf("%d %d %d", &a, &b, &m);
d=exgcd(a,m,&s,&t);//as+mt=gcd(a,m)=d
if(b%d) puts("无解");
else {
k=m/d;
s=b/d*s%k;
if(s<0) s+=k;
printf("解x≡%d",s);
for(int i=2,x=s+k; i<=d; i++,x+=k) {
if(i==d) printf(",%d(mod%d)\n",x,m);
else printf(",%d",x);
}
}
return 0;
}
9.计算中国剩余定理
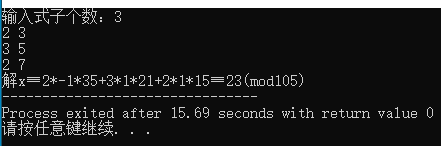
/*计算中国剩余定理*/
#include <stdio.h>
#define MAXN 1000
#define ll long long
ll exgcd(ll a,ll b,ll *x,ll *y){//ax+by=gcd(a,b)=d
if (!b) {
*x=1, *y=0;
return a;
}
ll d=exgcd(b,a%b,y,x);
*y-=a/b* *x;
return d;
}
ll CRT(ll b[],ll mod[],ll n,ll modn){
ll ans = 0;
printf("解x≡");
for(int i=0; i<n; i++){
ll x, y;
ll mi=modn/mod[i];
exgcd(mi,mod[i],&x,&y);
ans+=b[i]*x*mi;
if(i==0) printf("%ld*%ld*%ld",b[i],x,mi);
else printf("+%ld*%ld*%ld",b[i],x,mi);
}
ans%=modn;
if(ans<0) ans+=modn;
printf("≡%ld(mod%ld)",ans,modn);
return ans;
}
int main(){
ll b[MAXN],mod[MAXN];
ll n,modn=1,ans;
printf("输入式子个数：");
scanf("%d", &n);
for(ll i=0;i<n;i++){
scanf("%d %d", &b[i], &mod[i]);
modn*=mod[i];
}
CRT(b,mod,n,modn);
return 0;
}
10.模重复平方计算法
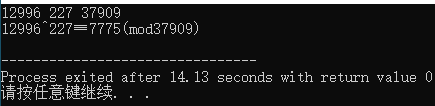
/*模重复平方计算法*/
#include <stdio.h>
#define ll long long
ll repeatMod(ll base,ll n,ll mod){
ll a=1;
while(n){
if(n&1){
a=(a*base)%mod;
}
base=(base*base)%mod;
n=n>>1;
}
return a;
}
int main(){
ll base,n,mod,ans;
scanf("%d %d %d", &base, &n, &mod);
ans=repeatMod(base,n,mod);
printf("%lld^%lld≡%lld(mod%lld)\n",base,n,ans,mod);
return 0;
}
11.高次同余式的提升
这个代码编译较慢，需要改进。
/*高次同余式的提升*/
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <math.h>
#define ll long long
#define MAXN 100
#define PRIME_NUM 20
int prime[MAXN];//素数表
typedef struct fx_info{
int freq;//次数
int coe;//系数
}fx_info;//f(x)次数系数
void find_prime(int num){//求前num个素数
prime[0]=2;
prime[1]=3;
prime[2]=5;
int j=3;
for(int i=1;;i++){
int num1=6*i+1,num5=6*i+5;
bool flag1=true,flag5=true;
for(int k=0;k<j;k++){
if(num1%prime[k]==0) flag1=false;
if(num5%prime[k]==0) flag5=false;
if(flag1==false&&flag5==false) break;
}
if(flag1) prime[j++]=num1;
if(j>=num) return;
if(flag5) prime[j++]=num5;
if(j>=num) return;
}
}
int find_p(int mod){//mod=p^a,求p
for(int i=0;i<PRIME_NUM;i++){
if(mod%prime[i]==0) return prime[i];
}
}
void deri(fx_info *fx,int len,fx_info *fx1,int *len1){//求导
for(int i=0;i<len;i++){
if(i==len-1){
if(fx[i].freq==0) break;
}
fx1[i].freq=fx[i].freq-1;
fx1[i].coe=fx[i].coe*fx[i].freq;
(*len1)++;
}
}
void disp(fx_info *fx,int len){//输出测试
for(int i=0;i<len;i++){
if(i==len-1){
if(fx[i].freq==0) printf("%d\n",fx[i].coe);
else printf("%dx^%d\n",fx[i].coe,fx[i].freq);
}
else printf("%dx^%d+",fx[i].coe,fx[i].freq);
}
}
int find_x1(fx_info *fx,int len,int p){//求f(x)≡0(modp)的解x1
ll sum;
for(int i=0;i<p;i++){
sum=0;
for(int j=0;j<len;j++){
sum+=pow(i,fx[j].freq)*fx[j].coe;
}
if(sum%p==0) return i;
}
}
int exgcd(int a,int b,int *x,int *y){//ax+by=gcd(a,b)=d，求a模b的可逆元x
if (!b) {
*x=1, *y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
*y-=a/b* *x;
return d;
}
int find_fx1x1modp(fx_info *fx1,int len1,int x1,int p){//求f'(x1) mod p的可逆元
ll sum=0;
int a;
for(int i=0;i<len1;i++){
sum+=pow(x1,fx1[i].freq)*fx1[i].coe;
}
a=sum%p;
int x,y;
exgcd(a,p,&x,&y);
return x;
}
int solve(fx_info *fx,int len,int x1,int x11,int p,int mod){
int x=x1,t,sum;
for(int i=1;;i++){
sum=0;
for(int j=0;j<len;j++){
sum+=pow(x,fx[j].freq)*fx[j].coe;
}
t=((ll)(-sum/pow(p,i)*x11))%p;
x=((ll)(x+t*pow(p,i)))%((ll)pow(p,i+1));
if (fabs((ll)pow(p, i+1) - mod) < 1e-9) {
return (int)(x % mod); // 确保返回的x小于mod
}
}
}
int main(){
int non_zero,non_zero1=0,freq,coe,freqH,mod,p,x1,x11,ans;
fx_info fx[MAXN],fx1[MAXN];
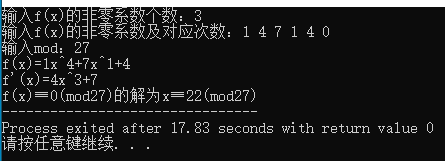
printf("输入f(x)的非零系数个数：");
scanf("%d", &non_zero);
printf("输入f(x)的非零系数及对应次数：");
for(int i=0;i<non_zero;i++){
scanf("%d %d", &coe, &freq);
if(i==0) freqH=freq;
fx[i].coe=coe;
fx[i].freq=freq;
}
printf("输入mod：");
scanf("%d", &mod);
find_prime(PRIME_NUM);//生成前PRIME_NUM个素数
p=find_p(mod);//mod=p^a,求p
deri(fx,non_zero,fx1,&non_zero1);
printf("f(x)=");
disp(fx,non_zero);
printf("f'(x)=");
disp(fx1,non_zero1);
x1=find_x1(fx,non_zero,p);
x11=find_fx1x1modp(fx1,non_zero1,x1,p);
ans=solve(fx,non_zero,x1,x11,p,mod);
printf("f(x)≡0(mod%d)的解为x≡%d(mod%d)",mod,ans,mod);
return 0;
}
12.求逆元
//a*inva≡1(mod b) 求a的逆元inva
#include <stdio.h>
int exgcd(int a,int b,int *x,int *y) { //ax+by=gcd(a,b)=d
if (!b) {
*x=1, *y=0;
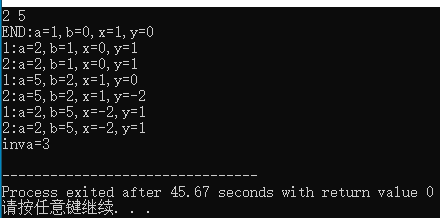
printf("END:a=%d,b=%d,x=%d,y=%d\n",a,b,*x,*y);
return a;
}
int d=exgcd(b,a%b,y,x);
printf("1:a=%d,b=%d,x=%d,y=%d\n",a,b,*x,*y);
*y-=a/b* *x;
printf("2:a=%d,b=%d,x=%d,y=%d\n",a,b,*x,*y);
return d;
}
int invmod(int a,int b){
int s,t,gcd;
gcd=exgcd(a,b,&s,&t);
if(gcd!=1){
printf("逆元不存在\n");
return 0;
}else{
if(s<0) s+=b;
return s;
}
}
int main() {
int a,b,inva;
scanf("%d %d", &a, &b);
printf("inva=%d\n",invmod(a,b));
return 0;
}
Keep it simple and stupid
