Splay指针版详解

经过一天RE的洗礼，终于把指针版\(\mathrm{Splay}\)赶出来了，泪目

看了一圈，居然没有找到\(\mathrm{Splay}\)的指针版题解，~~气抖冷，指针党什么时候才能站起来！~~

~~先放上自己的博客~~

一、总述

虽然都是平衡树，但是\(\mathrm{Splay}\)和\(\mathrm{Treap}\)是不一样的

\(\mathrm{Treap}\)维持平衡的条件是每个节点随机赋予的优先级，但\(\mathrm{Splay}\)没有这个条件

\(\mathrm{Splay}\)维持平衡的条件就是：把一个节点插入到最底之后，直接用splay操作旋转到根

虽然单次操作可能较慢，但是这样保证了整棵\(\mathrm{Splay}\)的期望树高为\(O(\log n)\)，总体复杂度是确定的，相较于\(\mathrm{Treap}\)来说更稳定

二、具体函数分析

（此处仅以某平衡树模板为例）

（提前说明，因为这是指针版，所以重心在于说明指针版可能出现的问题，关于splay或者rotate这些~~人尽皆知~~的函数的细节还烦请大家左转其它大佬的优质题解作进一步学习）

首先要说明，\(\mathrm{Splay}\)的很多函数是不需要递归的（区别于\(\mathrm{Treap}\)）

（以下以\(x\)代表上述题目中输入要求的操作的第二参数）

关于Splay的树节点

（这里提个醒，最后一行中的now和root这些非静态(non-static)的成员变量，在实际比赛中最好不要像我这样直接偷懒初始化（这种特性C++11以后才支持）
（建议写一个Splay的构造函数Splay(){now=tree,root=NULL;}解决这一问题）

struct Node
{
    int v,cnt,size;
    bool dir;
    Node *fa,*son[2];

    Node(){fa=son[0]=son[1]=NULL;cnt=size=0;}

    bool get_dir(){return ( fa?this==fa->son[1]:0 );}	//判断某节点是其父亲的左儿子还是右儿子（冒号后面的0对应没有父亲的情况，可以随便赋值） 

    void update()
    {
        size=cnt;

        if( son[0] ) size+=son[0]->size;
        if( son[1] ) size+=son[1]->size;return;
    }

}tree[maxn],*now=tree,*root=NULL;

insert

大概就是一直往下跳，一直跳到节点为空或者到达\(x\)本身所在的节点为止
赋值什么的都比较正常，就是要记得最后要把\(x\)对应的节点splay到根节点

（splay的细节在后面详述）

void insert(int x)
{
    Node *r=root,*fa=NULL;

    while( r and x!=r->v ) fa=r,r=r->son[x>r->v];

    if(r) r->cnt++;
    else
    {
        r=now++;
        r->v=x,r->size=r->cnt=1;
        r->son[0]=r->son[1]=NULL;

        r->fa=fa;
        if(fa) fa->son[x>fa->v]=r;
    }

    splay(r,NULL);return;
}

delete（为免与C++中的关键字冲突，建议将函数名仿照STL的习惯改为erase）
- 基本思想：先将\(x\)对应的节点的前驱（在本节中用\(l\)表示）splay到根节点，再将\(x\)对应的节点的后继（在本节中用\(r\)表示）splay到\(l\)的右儿子位置。
  - 此时，如果\(r\)和\(l\)都存在（理想状况下），根据平衡树的性质，\(r\)的左儿子就是我们要删除的节点
  - 但那只是理想情况，还有一些情况：
    1. 如果\(x\)没有后继（\(r\)为空），那么应该删除的节点应为l->son[1]
    2. 如果\(x\)既没有前驱，又没有后继，说明整棵\(\mathrm{Treap}\)中恰好只剩下root一个节点~~膝下无子~~，这时直接对root执行delete操作即可
  - ~~（所以实际操作时，delete代码往往最复杂）~~
- 抛开各种情况的话，delete本身操作不难，要不就是某节点->cnt-=1（cnt>1），要不就是某个节点=NULL（cnt==1），都是正常操作
- （注意！因为将某个节点=NULL时，这个节点对应的父子关系（例如在理想情况中，被删除的节点对应的是r->son[1]）也要被修改为NULL，所以在这种情况下，被删除的节点要加一个引用&，具体见下）
- （如果cnt>1的话，最后不要忘了splay）
```
void erase(int x)
{
    Node *l=get_lower(x),*r=get_upper(x);
    splay(l,NULL),splay(r,l);

    Node *&del=( (r or l)?(r?r->son[0]:l->son[1]):root );	//分三类（r->son[0],l->son[1]和root）讨论 

    if( del->cnt>1 ) del->cnt--,splay(del,NULL);
    else del=NULL;return;
}
```
get_lower(upper) & find
- （这里的find主要是借鉴了yybyyb大佬的博客Splay入门解析【保证让你看不懂（滑稽）】，在此作出著作权声明，侵改）
- 首先调用find(x)函数，得到\(x\)对应的节点并将其splay到根节点（这就是find函数的作用）
  
  如果树中没有\(x\)对应的节点的话，函数本身就会左右横跳，最后splay一个与\(x\)在数值上相邻的节点（可能比\(x\)大，也可能比\(x\)小）~~（大家看代码的时候感性理解一下）~~
- 然后又开始分类讨论（以下都以get_lower为例，get_upper只需要将大于小于号和左右儿子调换一下即可）：
  1. 如果splay上去以后的root刚好<x，此时的root就是x的前驱，直接返回root对应指针即可
  2. 如果是其他情况（root->v >= x），说明x节点本身不存在，那就要先将指针跳到root->son[0]（左儿子），再一直往右儿子的方向(son[1])跳（就是无限逼近root但又比root小），到达底端之后，返回最底端的节点的指针
```
Node *get_upper(int x)
{
    find(x);
    Node *r=root;

    if(!r) return NULL;
    if( r->v>x ) return r; 

    r=r->son[1];
    while( r and r->son[0] ) r=r->son[0];return r;
}

Node *get_upper(int x)
{
    find(x);
    Node *r=root;

    if(!r) return NULL;
    if( r->v>x ) return r; 

    r=r->son[1];
    while( r and r->son[0] ) r=r->son[0];return r;
}
```
  上面的两个函数的最后一行，两个判断条件已经很清晰了
  
  （通俗解释：如果r取了r->son[0]之后马上变成NULL，或者向左儿子横跳时发现，再往下一个左儿子r->son[0]==NULL，就退出循环，返回当前不等于NULL的节点）
get_rank
- 这个函数在实际操作中可以通过get_lower函数简化，所以前面才先介绍了get_lower函数
- 先用get_lower函数得到\(x\)节点的前驱对应的指针，然后将\(x\)的前驱splay到根节点
- 此时\(x\)节点的排名就是root->size - root->son[1]->size + 1 （相当于整棵树的大小减去右子树的大小再+1（因为\(x\)节点此时是root的右儿子，+1是要算上\(x\)自己））
- 注意，如果\(x\)没有前驱（get_lower返回的指针为NULL），请直接返回rank为\(1\)
```
int get_rank(int x)
{
    Node *u=get_lower(x);
    if(u) splay(u,NULL),u->update();
    return ( u?u->size-get_size(u->son[1]):0 )+1;
}
```
splay & rotate
- 不负众望~~吊了个大胃口~~，终于到了核心部分
- 其实到了splay反而不太想讲具体，因为大家能够点进来看题解，估计已经是~~身经百战~~或者看过许多其他dalao的数组版的题解，对splay的双旋有一定了解，所以这里就言简意赅：
  1. 本节点、父亲与祖父三点共线（没有拐弯），就先对父亲进行rotate，再对本节点进行rotate
  2. 不满足三点共线，就直接对本节点进行两次rotate
  不直接单旋，是因为直接单旋不能有效压低树高（如果你还有肝的话，建议自己模拟一下\(\mathrm{Splay}\)退化为链时直接单旋后树的形状，认识会更深刻）
- rotate本身的话（我知道很多同学觉得rotate很难记，和学\(\mathrm{Treap}\)），记住三条边即可（以左旋方向为0为例，右旋的话请将以下的左右儿子取反）：
  1. r 与 r->son[0]
  2. r->fa 与 r
  3. r->fa->fa 与 r->fa
- 修改后，上述边相应修改：
  1. r-fa-son[1]->r->son[0]
  2. r-son[0]->r->fa
  3. r->fa->fa对应的儿子改成r
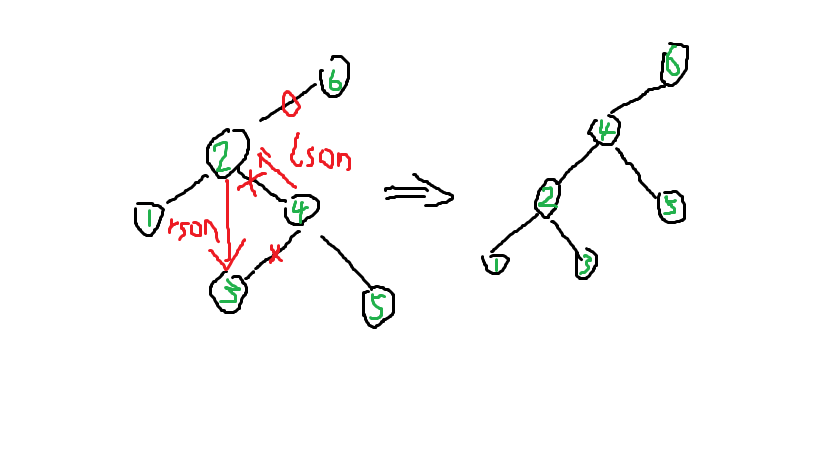
- ~~死记硬背+结合下图感性理解+即可~~
  
  （下图是对节点\(4\)的左旋）
- （代码中的link相当于在两个节点之间连边）
```
void link(Node *fa,Node *son,int d) //d决定son是fa的左儿子还是右儿子 
{
    if(fa) fa->son[d]=son;
    if(son) son->fa=fa;return;
}

void rotate(Node *r)
{
    Node *f=r->fa,*gf=f->fa;
    int dir1=r->get_dir(),dir2=f->get_dir();	//get_dir返回的是该节点是它的父亲的左儿子(0)或右儿子(1) 

    link(f,r->son[dir1^1],dir1);
    link(r,f,dir1^1); 
    link(gf,r,dir2);

    f->update(),r->update();return;	//注意，因为此时f是r的儿子，所以要先更新f节点再更新r节点！  
}

void splay(Node *r,Node *goal)	//r要一直splay到goal的儿子（goal为NULL时，r就splay到根节点） 
{
    if(!r) return;

    while(r->fa!=goal)
    {
        if( r->fa->fa!=goal ) rotate( r->get_dir()==r->fa->get_dir()?r->fa:r );	//判断是否三点共线，共线的话先rotate父节点
        rotate(r);
    }

    if( !goal ) root=r;return;	//goal为NULL，则r已经被splay到根节点，修改root为r 
}
```

get_kth

这个函数本身是最简单的，分三类讨论，注意向右儿子跳时要减去左儿子的size和节点本身的cnt，还有到最后不要忘了splay即可

int get_kth(int x)
{
    Node *r=root;
    if(r->size<x) return INT_MAX;	//特判

    while(1)
    {
        Node *l=r->son[0];

        if( get_size(l)+r->cnt<x ) x-=get_size(l)+r->cnt,r=r->son[1];
        else if( x<=get_size(l) ) r=l;
        else{splay(r,NULL);return r->v;}
    }
}

一个小函数
- get_size
  
  该函数返回某个节点的size，专门写一个函数是因为在get_kth函数中，左儿子的指针本身可能指向NULL，而众所周知，对NULL本身执行操作……无限RE预定
```
int get_size(Node *r){return ( r?r->size:0 );}
```

三、代码

#include<cstdio>
#include<ctime>
#include<cstdlib>
#include<climits>

const int maxn=1e5+2;

struct Splay
{
	struct Node
	{
		int v,cnt,size;
		bool dir;
		Node *fa,*son[2];
		
		Node(){fa=son[0]=son[1]=NULL;cnt=size=0;}
		
		bool get_dir(){return ( fa?this==fa->son[1]:0 );}	//判断某节点是其父亲的左儿子还是右儿子（后面的0是随便给的） 
		
		void update()
		{
			size=cnt;
			
			if( son[0] ) size+=son[0]->size;
			if( son[1] ) size+=son[1]->size;return;
		}
		
	}tree[maxn],*now=tree,*root=NULL;
	
	int get_size(Node *r){return ( r?r->size:0 );}
	
	void link(Node *fa,Node *son,int d) //d决定son是fa的左儿子还是右儿子 
	{
		if(fa) fa->son[d]=son;
		if(son) son->fa=fa;return;
	}
	
	void rotate(Node *r)
	{
		Node *f=r->fa,*gf=f->fa;
		int dir1=r->get_dir(),dir2=f->get_dir();	//get_dir返回的是该节点是它的父亲的左儿子(0)或右儿子(1) 
		
		link(f,r->son[dir1^1],dir1);
		link(r,f,dir1^1); 
		link(gf,r,dir2);
		
		f->update(),r->update();return;	//注意，因为此时f是r的儿子，所以要先更新f节点再更新r节点！  
	}
	
	void splay(Node *r,Node *goal)	//r要一直splay到goal的儿子（goal为NULL时，r就splay到根节点） 
	{
		if(!r) return;
		
		while(r->fa!=goal)
		{
			if( r->fa->fa!=goal ) rotate( r->get_dir()==r->fa->get_dir()?r->fa:r );	//判断是否三点共线，共线的话先rotate父节点
			rotate(r);
		}
		
		if( !goal ) root=r;return;	//goal为NULL，则r已经被splay到根节点，修改root为r 
	}
	
	void find(int x)	//查x并且splay到根节点 
	{
		Node *r=root;
		if(!r) return;
		
		while( x!=r->v and r->son[x>r->v] ) r=r->son[x>r->v];
		splay(r,NULL);return;
	}
	
//	void merge(Node *l,Node *r)
//	{
//		find(get_kth)
//		
//		splay(l,NULL);
//		l->son[1]=r,l->update();return;
//	}
//	
//	void split(int len,Node *&left,Node *&right)
//	{
//		if(root->size<len) return;
//		find(get_kth(len));
//		
//		left=root,right=root->son[1];
//		root->son[1]=NULL,root->update();return;
//	}

	int get_rank(int x)
	{
		Node *u=get_lower(x);
		if(u) splay(u,NULL);
		return ( u?u->size-get_size(u->son[1]):0 )+1;
	}
	
	int get_kth(int x)
	{
		Node *r=root;
		if(r->size<x) return INT_MAX;
		
		while(1)
		{
			Node *l=r->son[0];
			
			if( get_size(l)+r->cnt<x ) x-=get_size(l)+r->cnt,r=r->son[1];
			else if( x<=get_size(l) ) r=l;
			else{splay(r,NULL);return r->v;}
		}
	}
	
	void insert(int x)
	{
		Node *r=root,*fa=NULL;
		
		while( r and x!=r->v ) fa=r,r=r->son[x>r->v];
		
		if(r) r->cnt++;
		else
		{
			r=now++;
			r->v=x,r->size=r->cnt=1;
			r->son[0]=r->son[1]=NULL;
			
			r->fa=fa;
			if(fa) fa->son[x>fa->v]=r;
		}
		
		splay(r,NULL);return;
	}
	
	Node *get_lower(int x)
	{
		find(x);
		Node *r=root;
		
		if(!r) return NULL;
		if( r->v<x ) return r; 
		
		r=r->son[0];
		while( r and r->son[1] ) r=r->son[1];return r;
	}
	
	Node *get_upper(int x)
	{
		find(x);
		Node *r=root;
		
		if(!r) return NULL;
		if( r->v>x ) return r; 
		
		r=r->son[1];
		while( r and r->son[0] ) r=r->son[0];return r;
	}
	
	void erase(int x)
	{
		Node *l=get_lower(x),*r=get_upper(x);
		splay(l,NULL),splay(r,l);
		
		Node *&del=( (r or l)?(r?r->son[0]:l->son[1]):root );	//分三类（r->son[0],l->son[1]和root）讨论 
		
		if( del->cnt>1 ) del->cnt--,splay(del,NULL);
		else del=NULL;return;
	}
	
//	void run(Node *r)
//	{
//		if(!r) return;
//		
//		run(r->son[0]);
//		printf("%d(%d)",r->v,r->size);
//		run(r->son[1]);return;
//	}
}bt;

int main()
{
//	freopen("splay.in","r",stdin);
//	freopen("splay.out","w",stdout);
	
	int n;scanf("%d",&n);
	
	while(n--)
	{	
		int op,x;scanf("%d%d",&op,&x);
		
		switch(op)
		{
			case 1:bt.insert(x);break;
			case 2:bt.erase(x);break;
			case 3:
				printf("%d\n",bt.get_rank(x));break;
			case 4:
				printf("%d\n",bt.get_kth(x));break;
			case 5:
				printf("%d\n",bt.get_lower(x)->v);break;
			case 6:
				printf("%d\n",bt.get_upper(x)->v);break;
		}
	}
	
	return 0;
}

//1. get_lower和get_upper的r可能为空 
//2. get_rank时，因为是将u的左儿子rotate到根节点，所以应该是u->size - u->son[1]->size 
//3. erase时，要看r->son[0]和l->son[1]哪个存在 （注意加引用，因为可能要将del改为NULL）

几个困扰了我很久坑点在上面代码最后的注释里写了

ED：祝学习数据结构的各位能有一个~~肝疼的早上~~美妙的1A记录！

\(By\ the\ way\)，推荐大家以后用极限数据时，试试用climits这个库（我上面已经用了）

里面有许多数据类型的#define极限值，下面截取一部分供大家参考：

#include<climits>
#include<limits.h>
//...
#define INT_MIN (-2147483647 - 1)
#define INT_MAX 2147483647
#define UINT_MAX 0xffffffffU
#define LONG_MIN (-2147483647L - 1)
#define LONG_MAX 2147483647L
#define ULONG_MAX 0xffffffffUL
#define LLONG_MAX 9223372036854775807ll
#define LLONG_MIN (-9223372036854775807ll - 1)
#define ULLONG_MAX 0xffffffffffffffffull
//...

posted @ 2020-07-31 21:11 info___tion 阅读(413) 评论(1) 编辑收藏举报

刷新页面返回顶部

梦碎之境

Idolatrize World

Splay指针版详解

一、总述

二、具体函数分析

三、代码

公告