深入浅出网络流
最小割
最大权闭合子图
闭合子图是什么？
就是一个有向无环连通图。
最大权闭合子图就是说，图上的节点有正有负，我们要选出权值最大的点集。
建图过程：
- \(S\xrightarrow{w(i)} i\ (w(i)>0)\)
- \(i\xrightarrow{\infty} j\ ((i,j)\in E)\)
- \(i\xrightarrow{-w(i)}T\ (w(i)<0)\)
然后跑最大流，用\(\sum w(i)\ (w(i)>0)\)（所有正权点的权值和）减去求出来的最大流（最小割）就是答案。
为什么要这样呢？
分类讨论：
- 如果正权边被割了，那就说明在最小割中，正权边\(\leqslant\)对面的负权边（否则被割掉的就不会是正权边而是负权边），对应的情况就是：选了正权边之后，正权边所连通的负权边比正权边还大（在绝对值上），这样选就亏本了，所以才需要割掉（在代码中就是从正权点的权值和中减去）。
- 如果负权边被割了，就说明正权边比负权边大，选了之后不会亏本，割掉的只是选了这个正权点所付出的最小成本。
（感觉这个是最小割当中最好理解的了……）
8.6 老师提了一个挺有意思的模型：
有若干个活动，分别需要一些房子。使用房子有两种方式：
- 每个活动分别租一间
- 直接买一间，这样每个活动都能使用，不需要再额外租。
就是说，一个负权点的代价可以有不止一种形式。
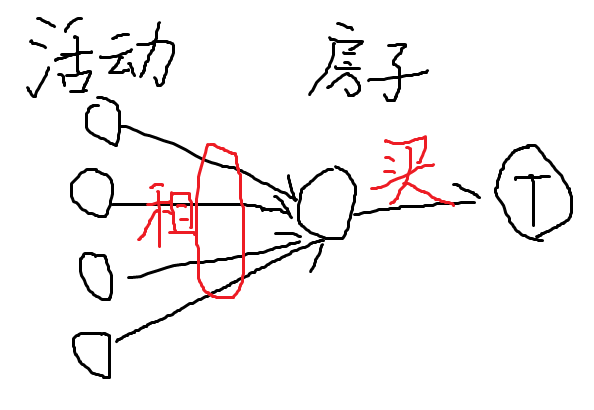
这样的话，原本那些连接正权点和负权点的，容量为\(\infty\)的边就有用了：
二选一模型
就是，一个节点有两种代价（或者收益），还有一些限制，让你找出最小的代价（最大的收益）
如果没有其他限制的话很简单：将两种代价（或者收益）一种连向\(S\)，另一种连向\(T\)，然后求出最小割，最小割就是最小的代价（如果是收益的话，就是必须要舍弃的最小收益）。
- 如果\(a\)被割给了\(S\)，\(b\)被割给了\(T\)，就有相应的代价；（双核CPU、善意的投票）
- 如果一个点集被割给了\(S\)，就有相应的收益；（寿司餐厅、Happiness、小M的作物）
- 如果一个点被割给了\(S\)，并且一个点集\(V'\)中有一个点被割给了\(T\)，就有相应的代价。
第一种
这样的话，求出最小割之后，割掉的就是最小的代价。
当然，像善意的投票就只需要根据意愿在\(S\)和\(T\)之间二选一即可（代价还是照样连）
第二种
代价是用来最小化的，所以用最小割可以直接解决，那收益呢？
没关系，可以先把收益都加起来，然后再把收益当成代价去建弧，跑最小割。
这样，割掉的就是最小的收益，剩下的收益自然就是最大的了。
第三种
（记不得老师讲什么了，自己脑补的）
（画反了，不想调）
（因为例题少所以就不讲了，反正最小割目前只接触了这两种模型）
二分图
\(\mathrm{DAG}\)最小路径覆盖
↑字面意思：用最少的路径（不是连接两个节点的边）覆盖\(\mathrm{DAG}\)上所有的点（两条路径不能经过相同的点）。
魔术球问题
可以发现，如果把能够组合成完全平方数的数对连边，就会形成一个或以上的独立的\(\mathrm{DAG}\)。
那问题就转化成了\(\mathrm{DAG}\)上的最小路径覆盖。
首先，因为对于一个数，有两种流量流入：一种是其他（比它小的）数想要和它组成完全平方数；另一种是它自己要和比它大的数组成完全平方数。
所以我们要将一个“数”拆成两个点：一个给比它小的点去连，另一个给它自己去连别人。
连边的话，将小数的点的入点连向大数的点的出点（前提是小数和大数的和是完全平方数），源点连向每个入点，每个出点连向汇点。
然后每次加入新数就连上相应的弧（比如将前面能够组成完全平方数的出点和入点连弧），再在先前的残量网络上直接跑最大流，如果最大流没有增加，说明这个数不能与之前的所有数组成完全平方数，就把柱子的数量加一即可。
事实上，一般的最小路径覆盖也是差不多和上面一样的，但如果要你直接输出最小路径数的话
就输出\((N-最大流)\)就可以了。（这个不难理解吧）
最小点覆盖 & 最大独立集
先来一波定义
点覆盖：G任意边都至少有一个顶点属于源点\(s\)的点集\(S\)；
独立集：G中两两互不相连的点集\(S\)。
最小点（权）覆盖：（点数/点权）最小的点覆盖；
最大点（权）独立集：（点数/点权）最大的点独立集。
最大流=最小割=最小点覆盖=\(N-最大独立集\)
上面很容易证：因为是最小割，所以只要把割边所连上的点删除，那么就能用最小的代价把\(s\)和\(t\)隔离开来。
可能还可以删掉其它的点（比如说你可以把和源点\(s\)直接相连的所有点都删掉，点集\(S\)就是与\(s\)直接相连的所有点），但是这样都没有最小割优。
然后，引入了一个点覆盖，就说明有一对点必须二选一，所以最大独立集就要\(-1\)，因为点与点之间互不相连。
如果是普通的最小点覆盖的话，容量设为\(1\)即可（当然，中间二分图的弧的容量还是\(\infty\)）。
如果是最小点权覆盖的话，把容量设为权值即可。
最后补充一个：二分图最大权匹配。
按照费用流跑即可（应该要把费用取为负数再跑）
