【比赛】【2019.8.1】
T1
不是很难,注意积雪高度的判断(要开long long)以及终点不需要特判即可。
#include<cstdio>
#include<cstring>
const int maxn=1e5+2;
struct Solution
{
struct Edge{int from,to,len;};
struct Graph
{
Edge edges[maxn*10];
int edge_cnt,Head[maxn],Next[maxn*10];
void add_edge(int from,int to,int len)
{
edges[++edge_cnt]=(Edge){from,to,len};
Next[edge_cnt]=Head[from],Head[from]=edge_cnt;return;
}
}G;
int bh[maxn],lh[maxn],ad;
long long dis[maxn],vis[maxn];
int S,T;
int Q[maxn*10];
void SPFA()
{
memset(dis,0x3f,sizeof(dis));
dis[S]=0;int h=0,t=0;Q[t++]=S;
while( h!=t )
{
int p=Q[h++];h%=maxn*5;
vis[p]=0;
for(int i=G.Head[p];i;i=G.Next[i])
{
Edge e=G.edges[i];
if( ( e.to==T or bh[e.to]+ad*( (long long)dis[p]+e.len )<=lh[e.to] ) and dis[p]+(long long)e.len<dis[e.to] )
{
dis[e.to]=dis[p]+e.len;
if( !vis[e.to] ) vis[e.to]=1,Q[t++]=e.to,t%=maxn*5;
}
}
}
return;
}
void solve()
{
int n,m,tl;scanf("%d%d%d%d%d%d",&n,&m,&S,&T,&tl,&ad);
for(int i=1;i<=n;i++) scanf("%d%d",&bh[i],&lh[i]);
for(int i=1;i<=m;i++)
{
int x,y,l;scanf("%d%d%d",&x,&y,&l);
G.add_edge(x,y,l),G.add_edge(y,x,l);
}
SPFA();
if( dis[T]<=tl ) printf("%d",dis[T]);
else printf("wtnap wa kotori no oyatsu desu!");
return;
}
}SOL;
int main()
{
SOL.solve();return 0;
}
T2
这个有点意思。
最短距离不难求,但是怎么求方案数呢?
if( dis[s][i]+dis[i][t]==dis[s][t] ) ans[s][t]+=ans[s][i]*ans[i][t];
上面的式子不难理解,但是实际题目中的写法必须是下面这样:
for(int i=1;i<=n;i++)
for(int s=1;s<=n;s++)
for(int t=1;t<=n;t++)
if( s!=i and i!=t and s!=t )
{
if( dis[s][i]+dis[i][t]<dis[s][t] )
{
dis[s][t]=dis[s][i]+dis[i][t];
ans[s][t]=ans[s][i]*ans[i][t];
}
else if( dis[s][i]+dis[i][t]==dis[s][t] ) ans[s][t]+=ans[s][i]*ans[i][t];
}
也就是说,我们要边求最短路边统计方案数。
为什么要这样呢?难道我不可以求完最短路再求方案数吗?
不可以。
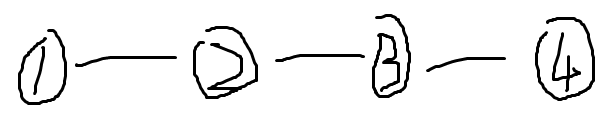
上面的例子,算完最短路之后,就会有两种“可行”的方案:
- (1-2) (2-3-4)
- (1-2-3) (3-4)
问题在于:对于有多个节点的最短路径,我们要找到表示它的唯一方法。
这也就是为什么要在求最短路的时候同时求方案数。
假设现在首先以\(2\)为中继点,那么我们就只能使\(1\to 3\)的方案数等于\(1\),至于\(2\to 4\)我们要不已经维护过了,要不就是维护不了的(因为不能把路径分解为\(2\to 2\)和\(2\to 4\),图上没有自环,而且当前\(2\to 4\)还没有被维护到)
然后,再枚举到以\(3\)为中继点的时候,就可以用\(1\to 3\)和\(3\to 4\)来表示\(1\to 4\)这条路径了。
(不用担心重复,重复的话意味着\(1\to 2\)和\(2\to 4\)也被统计了,但是这里以\(2\)为中继点的时候,我们还没有维护\(2\to 4\)啊,而且维护完\(2\to 4\)的时候我们也不会再去枚举回\(2\)了,所以不会重复)
扯了这么多,就是为了说明:要在求最短路的同时求方案数。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=102,maxm=9002;
struct Solution
{
int dis[maxn][maxn];
long long ans[maxn][maxn];
void solve()
{
memset(dis,0x3f,sizeof(dis));
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y,l;scanf("%d%d%d",&x,&y,&l);
dis[x][y]=l,ans[x][y]=1;
dis[y][x]=l,ans[y][x]=1;
}
for(int i=1;i<=n;i++)
for(int s=1;s<=n;s++)
for(int t=1;t<=n;t++)
if( s!=i and i!=t and s!=t )
{
if( dis[s][i]+dis[i][t]<dis[s][t] )
{
dis[s][t]=dis[s][i]+dis[i][t];
ans[s][t]=ans[s][i]*ans[i][t];
}
else if( dis[s][i]+dis[i][t]==dis[s][t] ) ans[s][t]+=ans[s][i]*ans[i][t];
}
for(int i=1;i<=n;i++)
{
double tmp=0.0;
for(int s=1;s<=n;s++)
{
for(int t=1;t<=n;t++)
{
if( s==i or i==t or s==t ) continue;
if( dis[s][i]+dis[i][t]==dis[s][t] ) tmp+=( (double)ans[s][i]*ans[i][t] )/ans[s][t];
}
}
printf("%.3lf\n",tmp);
}
return;
}
}SOL;
int main()
{
SOL.solve();return 0;
}
T3
其实理解成矩阵就很好理解了:
\(A\)矩阵和\(B\)矩阵分别表示经过\(x\)条边和\(y\)条边的矩阵,那么\(C=A\times B\)就是经过\(x+y\)条边的矩阵。
JZ res;
for(int i=1;i<=idx_cnt;i++)
for(int s=1;s<=idx_cnt;s++)
for(int t=1;t<=idx_cnt;t++)
res.a[s][t]=std::min( res.a[s][t],a[s][i]+op.a[i][t] );
return res;
和普通的\(Floyd\)算法不同的是,在这里,等式两边的矩阵是相互独立的。也就是说,\(C\)矩阵中的\(dis\)不会对\(A\)和\(B\)当中的产生影响,所以\(C\)矩阵是切切实实只表示\(x+y\)条边的矩阵。
而\(Floyd\)算法中,用\(1\)条边的信息统计完\(2\)条边的信息之后,\(2\)条边的信息又要马上在\(dis\)数组里面用来统计\(3\)条、\(4\)条边的信息,所以不是独立的。
知道具体含义之后就可以矩阵快速幂了:
#include<cstdio>
#include<cstring>
#include<algorithm>
int idx[1002],idx_cnt;
struct JZ
{
int a[105][105];
JZ(){memset(a,0x3f,sizeof(a));}
JZ operator * (const JZ &op)
{
JZ res;
for(int i=1;i<=idx_cnt;i++)
for(int s=1;s<=idx_cnt;s++)
for(int t=1;t<=idx_cnt;t++)
res.a[s][t]=std::min( res.a[s][t],a[s][i]+op.a[i][t] );
return res;
}
JZ operator *= (const JZ &op)
{
*this = (*this)*op;
return *this;
}
};
int main()
{
JZ dis;
int K,m,S,T;scanf("%d%d%d%d",&K,&m,&S,&T);
for(int i=1;i<=m;i++)
{
int len,x,y;scanf("%d%d%d",&len,&x,&y);
if( !idx[x] ) idx[x]=++idx_cnt;
if( !idx[y] ) idx[y]=++idx_cnt;
dis.a[idx[x]][idx[y]]=dis.a[idx[y]][idx[x]]=len;
}
JZ ans=dis;--K;
while(K)
{
if( K&1 ) ans*=dis;
dis*=dis;K>>=1;
}
printf("%d",ans.a[idx[S]][idx[T]]);
return 0;
}
T4
最短路+计算几何是真的神奇。
首先,那些所在直线会穿过被保护节点(把它们分成两部分)的线段是不能建边的(要不就是真的穿过了,要不就是没有穿过,但是方向不对,选了之后会多绕一条线段)
然后就要单向建边。
例如,如果对于\(\overrightarrow{AB}\),所有被保护节点都在它的右边(也可以与它共线),那么就可以直接从\(A\)连一条边到\(B\)。
其实这样做是为了求有向图最小环(无向图的太难了,偷懒嘛)。
有向图最小环就很简单,直接\(Floyd\)之后,\(dis(i,i)\)就是经过\(i\)点的最小环的长度。
无向图最小环另外讲。
#include<cstdio>
#include<cstring>
#include<algorithm>
const int maxn=502;
struct Solution
{
struct Point
{
int x,y;
Point(int x=0,int y=0){this->x=x,this->y=y;}
void read(){scanf("%d%d",&x,&y);return;}
};
typedef Point Vector;
Vector make_vec(Point s,Point t){return Vector(t.x-s.x,t.y-s.y);}
int Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
Point P1[maxn],P2[maxn];
int dis[maxn][maxn];
bool solve()
{
memset(dis,0x3f,sizeof(dis));
int n1;if( scanf("%d",&n1)==EOF ) return 0;
for(int i=1;i<=n1;i++) P1[i].read();
int n2;scanf("%d",&n2);
for(int i=1;i<=n2;i++) P2[i].read();
for(int s=1;s<=n2;s++)
for(int t=1;t<=n2;t++)
{
if( s==t ) continue;
bool flag=1;
for(int k=1;k<=n1;k++)
if( Cross( make_vec( P2[s],P2[t] ),make_vec( P2[s],P1[k] ) )>0 ){flag=0;break;}
if(flag) dis[s][t]=1;
}
for(int i=1;i<=n2;i++)
for(int s=1;s<=n2;s++)
{
if( dis[s][i]==0x3f3f3f3f ) continue;
for(int t=1;t<=n2;t++)
dis[s][t]=std::min( dis[s][t],dis[s][i]+dis[i][t] );
}
int ans=0x3f3f3f3f;
for(int i=1;i<=n2;i++) ans=std::min( ans,dis[i][i] );;
if( ans>n2 ) puts("ToT");
else printf("%d\n",n2-ans);
return 1;
}
}SOL;
int main()
{
while( SOL.solve() );return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号