SA学习笔记

（二）倍增+基数排序

这个就难咯

首先必须插播一段基数排序的基本概念：

比如说有一堆两位数要你去排序，基数排序的步骤就是。

1. 开一个能装得下值域的桶\(\mathrm{sum}\)（在这里开到\(10\)就可以了）

2. 把每个数的个位存进桶里

3. 把桶改成前缀和的形式

4. 然后以原数组的顺序从大到小枚举每个数，然后这个数的部分的排名就是\(sum(a(i)\mod 10)\)（\(\mathrm{a(i)}\)表示枚举到的那个数，\(\mathrm{i}\)是下标）。

   在这里为了方便排序，我们要开一个数组\(\mathrm{rank}\)，\(\mathrm{rank(i)}\)表示排名为\(\mathrm{i}\)的数在原数组中的位置。

   具体操作就是rank[ sum[a[i]%10]-- ]=i;

   减去\(\mathrm{sum}\)是因为把数字填进去了之后就少了个数，之后再出现相同的数要往前放。

   这里说一下为什么要从大到小枚举每个数：因为\(\mathrm{sum}\)代表的是总和，如果出现相同的数，那么排名肯定是取最大的，为了保证排序算法的正确和稳定性，才需要倒序枚举。

5. 做完了之后，把个位换成十位，转回\(2\)，然后第\(4\)步要变一下：枚举时的下标不是在原数组中枚举，而是在\(\mathrm{rank}\)数组中枚举。

插播完毕，现在讲讲怎么构造后缀数组：

1. 粗暴地把长度为\(1\)的\(\mathrm{sa}\)搞出来，这个很简单，直接像桶排一样把每个数放进桶里面，然后像基数排序一样倒序枚举，把每个下标放进\(\mathrm{sa}\)里面即可（因为\(\mathrm{sa}\)的下标的意义就是排名）。

2. 开始构造长度为\(2\)的\(\mathrm{sa}\)。因为要基数排序，我们要先对第二关键字排序，所以我们要开多一个数组\(\mathrm{key2}\)，它的作用和基数排序里面的\(\mathrm{rank}\)一样，都是存储部分有序的下标。

   • 因为最后的几个后缀的第二关键字是空的，所以它们要优先放进\(\mathrm{key2}\)里面。

   • 然后再以\(\mathrm{sa}\)中的下标的顺序去枚举，因为\(\mathrm{sa}\)已经帮我们把各个后缀的位置按字典序排好了，我们直接枚举\(\mathrm{sa(i)}\)也是为了保证\(\mathrm{key2}\)的有序。此外要注意，如果\(\mathrm{sa(i)]}\)小于等于构造的长度的一半，那这个第二关键字就是没用的（因为它的第一关键字为空，但第一关键字是不能为空的）

   • 填好\(\mathrm{key2}\)后，接下来的操作其实和第一步中的“粗暴”基数排序很像了！（但这一段的代码也是最难理解的）

     说明白一点，其实只有一点不一样：

   外面的基数排序在把下标填进排名数组时，填进去的下标就是\(\mathrm{i}\)，但是这里的操作填的下标是\(\mathrm{key2(i)}\)罢了。

   这其实和基数排序的流程一样的：基数排序在排完个位后继续排十位时，枚举的下标不是在原数组中的\(n\sim 1\)，而是在\(\mathrm{rank}\)数组中的\(n\sim 1\)罢了。就这么简单！

   具体是怎样的下面会放代码。

   • 之后还有一些步骤，但都不是难点了，这里就不多说了。心累。

3. 然后继续构造长度为\(4,8,16…\)的\(\mathrm{sa}\)。

就这么简单！

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn=1000005;

struct Suffix_Array
{
	char s[maxn];
	int len;

	int sa[maxn],key2[maxn];
	int rank[maxn],new_rank[maxn];

	int sort_sum[maxn];

	int height[maxn];

	bool equal(int x,int y,int l)
	{
		if( rank[x]^rank[y] ) return false;
		if( ( x+l>len and y+l<=len ) or ( x+l<=len and y+l>len ) ) return false;
		if( x+l>len and y+l>len ) return true;
		return rank[x+l]==rank[y+l];
	}

	void Make_SA()
	{
		int m=256;

		for(int i=1;i<=len;i++) rank[i]=s[i];
        //==============1
		for(int i=0;i<m;i++) sort_sum[i]=0;

		for(int i=1;i<=len;i++) sort_sum[rank[i]]++;
		for(int i=1;i<m;i++) sort_sum[i]+=sort_sum[i-1];

		for(int i=len;i>=1;i--) sa[ sort_sum[rank[i]]-- ]=i;
        //==============1

		for(int l=1;l<len;l<<=1)
		{
			int sz=0;
			for(int i=len-l+1;i<=len;i++) key2[++sz]=i;

			for(int i=1;i<=len;i++)
				if( sa[i]>l ) key2[++sz]=sa[i]-l;
			//==============2
			for(int i=0;i<m;i++) sort_sum[i]=0;
			
			for(int i=1;i<=len;i++) sort_sum[ rank[i] ]++;
			for(int i=1;i<m;i++) sort_sum[i]+=sort_sum[i-1];

			for(int i=len;i>=1;i--)
				sa[ sort_sum[rank[key2[i]]]-- ]=key2[i];
            //==============2

			new_rank[ sa[1] ]=1;
			int cnt=1;

			for(int i=2;i<=len;i++)
			{
				if( !equal(sa[i],sa[i-1],l) ) cnt++;
				new_rank[sa[i]]=cnt;
			}

			for(int i=1;i<=len;i++) rank[i]=new_rank[i];

			if( cnt==len ) break;
			m=cnt+1;
		}

		return;
	}

	void Make_Height()
	{
		int k=0;

		for(int i=1;i<=len;i++)
		{
			if( rank[i]==1 ) continue;
			k=max(k-1,0);

			while( s[sa[ rank[i] ]+k]==s[sa[ rank[i]-1 ]+k] ) k++;
			height[rank[i]]=k;
		}

		return;
	}
	
}SA;

int main(int argc, char const *argv[])
{
	scanf("%s",SA.s);
	SA.len=strlen(SA.s);

	for(int i=SA.len;i>=1;i--) SA.s[i]=SA.s[i-1];

	SA.Make_SA();

	for(int i=1;i<=SA.len;i++)
		printf("%d ",SA.sa[i]);

	return 0;
}

大家应该能发现，1和2这两部分几乎完全一样！只不过把下标填进\(\mathrm{sa}\)里面时\(\mathrm{rank(i)}\)变成了\(\mathrm{rank(key2(i))}\)而已。大家结合之前的讲解应该就能明白这堆代码是在干什么了。

然后2下面那部分就是说，我们要按照\(\mathrm{sa}\)中的下标的顺序去枚举下标（因为刚才已经排好序了），然后再调用\(\mathrm{rank}\)去看这两个下标的第一关键字的排名和第二关键字的排名是否相同，相同的话，新的\(\mathrm{new\_rank}\)就\(+1\)而已。不难理解

最后再把\(\mathrm{new\_rank}\)memcpy到\(\mathrm{rank}\)中就可以了。

m=cnt是把桶的大小改成排名的大小。

对，完了，这就是最基本的后缀排序算法！其实没有那么难！

最后补一下坑点：

1. 用注释标了“2”的那部分可能有些难懂。

2. new_rank[ sa[1] ]=1;
   int cnt=1;
   
   for(int i=2;i<=len;i++)
   {
   	if( !equal(sa[i],sa[i-1],l) ) cnt++;
   	new_rank[sa[i]]=cnt;
   }
   

   这一段代码很容易把\(\mathrm{new\_rank[sa[i]]}\)打成\(\mathrm{new\_rank[i]}\)。

---

（三）\(\mathrm{Height}\)数组

有了上面这些，其实你能做的东西很少。所以我们需要一个更加强大的数组：\(\mathrm{Height}\)数组。

\(\mathrm{Height[i]}\)的定义为\(\mathrm{LCP(suffix(sa(i-1)),suffix(sa(i)))}\)，也就是\(\mathrm{suffix(sa(i-1)),suffix(sa(i))}\)两个后缀的最长公共前缀（\(\mathrm{the\ Longest\ Common\ Prefix}\)）的长度。

如果直接按照\(\mathrm{sa}\)的顺序去算的话，时间复杂度是\(O(n^2)\)的，需要考虑更快的方法。

首先，\(\mathrm{Height}\)数组有两个很重要的性质：

1. \(\mathrm{LCP(suffix(i),suffix(j))=\min{Height[k]} \ |\ rank(i)<k\leqslant rank(j) }\)
2. \(\mathrm{Height[rank[i]]\geqslant Height[rank[i]-1]-1}\)

第一条性质说明了任意两个后缀的\(\mathrm{LCP}\)可以转化成静态区间最值问题，也就是\(\mathrm{RMQ}\)。

第二条性质更强，它告诉我们：如果我们按\(\mathrm{rank}\)中排名的顺序去算\(\mathrm{Height}\)数组的话，时间复杂度可以降为\(O(n)\)，证明的方法和\(\mathrm{KMP}\)比较像，因为时间复杂度都是均摊的。

---

（四）后缀数组的应用

1.最长公共前缀

给定一个字符串，询问某两个后缀的最长公共前缀。

这个直接利用\(\mathrm{Height}\)数组的第一个性质，就可以转化成一个\(\mathrm{RMQ}\)问题了。

2.可重叠最长重复子串

给定一个字符串，求最长重复子串，这两个子串可以重叠。

这个更简单，答案就是\(\mathrm{Height}\)数组中的最大值。

3.不可重叠最长重复子串*

给定一个字符串，求最长重复子串，这两个子串不能重叠。

这个就没这么简单了。

首先可以发现答案可以二分，所以这一题可以转化成判定问题。

然后，假设我们要知道存不存在长度为\(k\)的不重叠的重复子串。

我们先把\(\mathrm{Height}\)数组搬回出来：

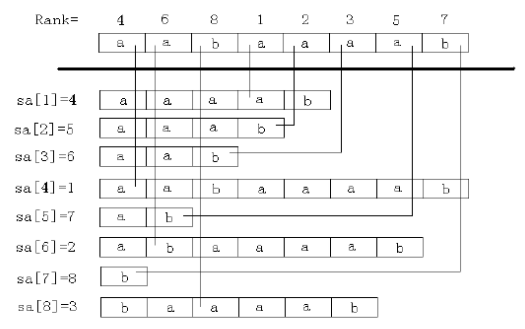
我们把\(\mathrm{Height}\)数组中的后缀分成若干组，其中每组的后缀之间的 \(\mathrm{Height}\)值都
不小于二分的长度\(k\)。

然后对于每一组后缀，看看这些后缀的\(\rm sa\)的值的极差是否\(\mathrm{\geqslant k}\)，是则说明存在长度为\(k\)的不重叠重复子串。

其实很容易解释上面这些：

1. 为什么要分组？

   很容易证明，分出来的每一组后缀，它们的\(\mathrm{LCP}\)肯定不一样（注意这里指的就是\(\mathrm{LCP}\)而不是\(\mathrm{LCP}\)的长度），这样分组是为了更好地分步判定。

2. 为什么每一组中\(\mathrm{sa}\)值的极差\(\mathrm{\geqslant k}\)就表示找到了。

   这个也很好懂。\(\mathrm{sa(i)}\)是排名为\(i\)的后缀的位置。\(\mathrm{sa}\)值的极差\(\mathrm{\geqslant k}\)，就说明这一组当中离得最远的两个后缀的距离也\(\mathrm{\geqslant k}\)，它们也就不会重叠了，所以就说明我们找到了。

这个问题也不算难，但是是第一道要充分利用\(\mathrm{Height}\)数组的性质的例题。

例题：\(\mathrm{POJ1743}\) \(\mathrm{P2743}\)

4.可重叠的至少出现\(k\)次的最长重复子串

给定一个字符串，求至少出现\(k\)次的最长重复子串，这\(k\)个子串可以重叠。

第一个自己想出来的模型。

这一题还比上一题简单一点。还是先二分，然后把\(\mathrm{Height}\)数组分组，然后看一下有没有哪一个组的后缀的数量是\(\geqslant k\)的即可。

例题：\(\mathrm{POJ3261}\) \(\mathrm{P2852}\)

有个坑点：一个\(\mathrm{Height}\)代表的是两个后缀，所以在分完组计算后缀个数的时候要再\(+1\)

5.不相同的子串的个数

给定一个字符串，求不相同的子串的个数。

不难发现每个子串都是某个后缀的前缀，于是问题转化成了后缀之间的不同前缀个数。

因为按照\(\mathrm{sa}\)排列好的后缀是有字典序的，所以相邻两个后缀是最相似的（也就是\(\mathrm{LCP}\)的长度最长的），所以我们直接按照\(\mathrm{sa}\)的顺序计算每个后缀的“贡献”。

首先，一个后缀最多能贡献\(\mathrm{n-sa(i)+1}\)个后缀，然后还要减去和它在\(\mathrm{sa}\)中相邻的后缀的公共前缀数，这不就是\(\mathrm{Height}\)数组吗？所以最终贡献就是$$\mathrm{\sum\limits_{i=1}^{n} (n-sa(i)+1)-Height(i)}$$

为什么不需要考虑\(i\)和\(i-2\)的？因为已经被\(i\)和\(i-1\)、\(i-1\)和\(i-2\)包含了

例题：\(\mathrm{SPOJ705}\)

6.最长回文子串

给定一个字符串，求最长回文子串。

这个也不难，把字符串翻转之后接在原字符串后面，中间再插入一个不相关的字符，然后我们直接枚举字符串的每个位置，然后计算以这个位置为中心的最长回文子串（当然，奇回文和偶回文都要考虑）。

具体方法就是找到这个位置关于最中间那个不相关字符的对称点，然后奇回文就是这个对称点的后缀与原位置的后缀的\(\mathrm{LCP}\)，偶回文就是对称点的后一个点。

坑点：

1. 用\(\mathrm{RMQ}\)预处理的时候总是记错\(\mathrm{Height}\)数组的性质（把\(\min\)记成了\(\max\)）
2. 因为枚举的是回文子串的中心位置，所以子串长度和子串开头位置都要再计算一次。

例题：\(\mathrm{Ural\ 1297}\)

9.最长公共子串

给定两个字符串\(\mathrm{A}\)和\(\mathrm{B}\)，求最长公共子串。

注意啊，是最长公共子串，不是最长公共子序列。

这个和6.最长回文子串有点像，也是要把一个字符串接到另一个的后面，中间再插一个不相关的字符。然后我们就可以按照\(\mathrm{sa}\)的顺序去扫\(\mathrm{Height}\)数组了。

那么答案是否就是\(\mathrm{Height}\)数组的最大值呢？不！因为有些排名相邻的后缀的开头位置是在同一个字符串里的！不过这个也不难，只需要我们在扫描每个\(\mathrm{Height(i)}\)时，比较一下\(\mathrm{sa(i)}\)和\(\mathrm{sa(i-1)}\)是否在同一个字符串内即可。

例题：\(\mathrm{POJ\ 2774}\)

10.长度不小于\(k\)的公共子串的个数**

给定两个字符串\(\mathrm{A}\)和\(\mathrm{B}\)，求长度不小于\(k\)的公共子串的个数（可以相同）。

从这道题开始程序的细节会开始变得巨多……因为要维护的东西不是多就是很复杂难懂。

俗话说得好，不 懂 变 量 操 作 就 不 要 装 \(\mathrm{A}\) \(\mathrm{C}\)。

还是套路，将两个字符串拼起来，中间用一个没有出现过的字符隔开，然后求\(\mathrm{sa}\)和\(\mathrm{Height}\)，然后再把\(\mathrm{Height}\)按\(k\)分组。

然后我们把答案分成两类：

1. 查\(\mathrm{A}\)的后缀在前面，\(\mathrm{B}\)的后缀在后面的方案数。
2. 查\(\mathrm{B}\)的后缀在前面，\(\mathrm{A}\)的后缀在后面的方案数。

这里的和下文中的“前面”指的都是是后缀的排名靠前。

这样的话，对于每个后缀，我们只要算出 在它前面 并且 和它不在同一个字符串中 的后缀的\(\mathrm{LCP}\)的长度即可。这个可以直接利用\(\mathrm{Height}\)的性质用\(\mathrm{RMQ}\)求出。

但是一个个查\(\mathrm{LCP}\)的时间复杂度是\(O(n^2)\)的，乌龟一样。所以我们要考虑优化。

手动模拟一下暴力算法的过程，就会发现：如果当前遇到了一个很小的\(\mathrm{Height}\)的话，那么在统计答案时，前面比这个\(\mathrm{Height}\)大的\(\mathrm{Height}\)全都要改小。

等等，遇到小的数就把大的数改小……这不是单调栈吗？

所以我们就可以维护一个以\(\mathrm{Height}\)为关键字的单调栈，然后像上面一样，如果当前\(\mathrm{Height}\)的值\(\leqslant\)栈顶的\(\mathrm{Height}\)，就把栈顶的\(\mathrm{Height}\)弹出栈。

但程序实现没有这么简单。因为你要算出单调栈中每个\(\mathrm{Height}\)所代表的后缀的数量（因为同一个\(\mathrm{Height}\)可能有多个对应的后缀，比如说有三个后缀\(aaaa\),\(aaaab\),\(aaaac\)，它们的\(\mathrm{Height}\)都是\(4\)，但是在计算答案时这三个后缀都有贡献），而且你在遇到一个很小的\(\mathrm{Height}\)时要把栈顶的元素全都改小。

所以单调栈里面存的要是一个双关键字的结构体，第一关键字是\(\mathrm{Height}\)，第二关键字是这个\(\mathrm{Height}\)包含的后缀的数量。

然后在单调栈中插入元素时，我们要开多一个临时结构体变量，当栈中元素弹出时，把这个元素的第二关键字（后缀的数量）加进那个临时变量的第二关键字中。

但是这样还是不行，当你查询答案时，你还是要遍历一次单调栈，时间复杂度没变。

所以我们要多开一个变量维护单调栈中的答案，维护很简单，弹出元素时减去元素一二关键字的积，加入元素时加上即可。

然而，细节还没讲完，在开临时结构体变量时，我们要这样赋初值：

Data tmp( height[i],sa[i-1]>mid );	//算A串的答案
Data tmp( height[i],sa[i-1]<mid );	//算B串的答案

为什么是\(\mathrm{sa[i-1]}\)呢？因为两个后缀的\(\mathrm{LCP}\)是这样求出的：

\[\mathrm{LCP(suffix(i),suffix(j))=\min{Height[k]} \ |\ rank(i)<k\leqslant rank(j) } \]

假如\(\mathrm{Height(i)}\)是某个\(\mathrm{LCP}\)式子中的编号最小的\(\mathrm{Height}\)，那么它代表的\(\mathrm{suffix(i)}\)就应该是\(\mathrm{sa(i-1)}\)。

第一道要我放代码去记的\(\mathrm{SA}\)题。

\(\mathrm{Code}\)

例题：\(\mathrm{POJ\ 3415}\) \(\mathrm{P3181}\)

11.不小于\(k\)个字符串中的最长子串*

给定\(n\)个字符串，求出现在不小于\(k\)个字符串中的最长子串。

首先把\(n\)个字符串拼起来，中间用字符串中不会出现的字符隔开，而且这些字符要互不相同。

还是套路二分答案+\(\mathrm{Height}\)数组分组，然后对于每一组后缀，我们可以开一个\(\mathrm{vis}\)数组去记录这些后缀在哪些字符串（之前不是把\(n\)个字符串拼在一起了吗）中出现过，然后算完一组后缀之后看看这组后缀是否在\(\geqslant k\)个字符串中出现过即可。

坑点：

1. 中间相隔的字符不能相同。
2. 多组数据不要忘了初始化。
3. 二分答案时上界不要弄错（我以为是字符串的最短长度，但要用最长长度才是对的）

12.每个字符串至少出现两次且不重叠的最长子串*

给定\(n\)个字符串，求在每个字符串中至少出现两次且不重叠的最长子串.

这个和3.不可重叠最长重复子串也很像，只不过还是要先来一波套路操作，把\(n\)个字符串拼在一起，中间用字符串中不会出现的字符隔开，而且这些字符要互不相同。

然后就二分子串的长度，然后再按照子串的长度给\(\mathrm{Height}\)中的后缀分组，这里要维护两个数组\(\mathrm{min\_pos[i],max\_pos[i]}\)，表示当前这一组后缀中，位于第\(i\)个字符串（之前不是把\(n\)个字符串拼在一起了吗）的后缀的开头位置的最大值和最小值。

维护好一组的\(\mathrm{min\_pos,max\_pos}\)之后，就直接扫描这两个数组。

• 如果两个数组中有哪个位置是没有访问过的，说明这组后缀没有在所有字符串中出现过
• 如果\(\mathrm{max\_pos[i]-min\_pos[i]<}\)二分的长度，说明这组后缀在某个字符串中一定没有不重叠的相同子串。

仅当上面这两个条件都不满足时，二分的这个长度才合法。

坑点：

1. 多组数据不要忘了初始化。
2. 在\(\mathrm{Height}\)数组中扫描时，如果要将\(\mathrm{Height}\)数组的下标转回原字符串的下标的话，要用\(\mathrm{sa[i]}\)转换而不能直接用\(\mathrm{i}\)。