基础数据结构~
基础数据结构
飞速刷题进行时~
markdown果然好用w
0x11栈
我到底是什么时候写的前两道题???
·火车进站
居然只要求输出路线....
那么只能用递归法:
对于每一个状态,显然的我们只有两种选择:
1、把下一个数进栈
2、把当前数出栈(栈非空)
时间复杂度O(\(2^N\))
代码:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=30;
int zh[N],ans[N],top=0,cz=0,num=0,n;//栈数组、答案数组、栈顶
void dfs(int x)
{
if(x==n+1)
{
if(num>=20)
exit(0);
num++;
for(int i=1;i<=cz;i++)
printf("%d",ans[i]);
for(int i=top;i>=1;i--)
printf("%d",zh[i]);//把没出栈的一次性出了
printf("\n");
return;
}
if(top)//栈非空
{
ans[++cz]=zh[top--];
dfs(x);
zh[++top]=ans[cz--];
}
top++;
zh[top]=x;
dfs(x+1);
top--;
}
int main()
{
scanf("%d",&n);
dfs(1);
return 0;
}
·火车进出栈问题
当我在思考这个该用递推还是DP的时候,猛然发现这其实是高精度...
显然的,这道题得用高精度卡特兰数...
由于卡特兰数是0x36的内容,我们在这里只浅显的了解一下公式与算法:
Catalan数
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,满足任意前缀中0的个数都不少于1的个数的序列的数量为:
\(Cat_n=\cfrac{C^n_{2n}}{n+1}\)
可以形象的理解为从原点出发,每次向x或y轴正方向移动1单位,到达点(n,n),且在移动过程中除两个端点外不接触直线y=x的移动方案数。
有递推式:
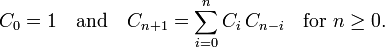
也满足:
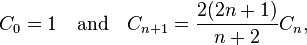
具体推导过程此处暂时不提,可以参看百度百科。
n的范围是[1,60000],如果直接用高精度数组存会因为超时长爆炸,所以此处需要使用高精度压位。
普通高精度是使用数组存储的,每个位置存储一个数字,这显然会造成很大的时间和空间浪费。
压位高精度就是将每个位置存储的数字数增加,如变为4个或5个,这样可以有效节省空间。
由于要使用高精度计算卡塔兰数,我们选用\(Cat_n=\cfrac{C^n_{2n}}{n+1}=\frac{n*(n+1)*(n+2)*...*(2n)}{1*2*...*n}*\frac{1}{n+1}\)这个公式
同时为避免高精度除法,使用分解质因数的做法,即把分子、分母快速分解质因数,在数组中保存各质因数的指数,然后把分子分母的指数对应相减(将分母消去),最后使用高精乘低精把剩余质因子乘起来。
具体实现:
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef unsigned long long ll;
const ll M=1e9;//压位最大值,由于是低精乘高精,所以使用九位
const int N=6e4+10;
int k=1;//最高位
ll gao[N],pri[N*2];//高精数组、质因子
void prime(int x,int f)//质因数分解
{
for(int i=2;i*i<=x&&x!=1;i++)
{
while(x%i==0)
{
pri[i]+=f;
x/=i;
}
}
if(x>1)
pri[x]+=f;
}
void cheng(ll c)//高精压位乘
{
for(int i=1;i<=k;i++)
gao[i]*=c;
for(int i=1;i<=k;i++)
{
gao[i+1]+=gao[i]/M;
gao[i]=gao[i]%M;
}
while(gao[k+1])
k++;
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)//分子
prime(n+i,1);
for(int i=2;i<=n+1;i++)//分母
prime(i,-1);
gao[1]=1;//必要步骤,不然输出都会为0
for(int i=1;i<=2*n;i++)
{
for(int j=1;j<=pri[i];j++)
cheng(i);
}
printf("%lld",gao[k]);//输出最高位(不带前导零)
for(int i=k-1;i>=1;i--)//整体倒序,数组内正序
printf("%09lld",gao[i]);//除最高位外均输出九位
return 0;
}
·直方图中最大的矩形
上一道题真的好麻烦终于来到下一道了ohhhhh
维护一个单调递增的高度栈,如果比当前矩形高则直接进栈
若低则不断弹出栈顶直到高度小于或等于该高度,并标记最高高度为该矩形,并不断累计宽度
出栈结束后将一个高度为最高高度,宽度为累计值的矩形入栈,再依照上述方法更新最大值。
详解见这里 我真是懒得画图了orz
代码
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef unsigned long long ll;
const int N=1e5+10;
int top;
ll a[N],zhan[N],ans,w[N],n;//w[top]表示栈顶为top时栈顶矩形的宽度
void work()
{
int kuan;
ans=0;
a[n+1]=top=0;
for(int i=1;i<=n+1;i++)
{
if(a[i]>zhan[top])
{
top++;
zhan[top]=a[i];
w[top]=1;
}
else
{
kuan=0;
while(zhan[top]>a[i])//栈顶元素大于入栈元素
{
kuan+=w[top];
ans=max(ans,(ll)kuan*zhan[top]);//注意此处的最大值是当前栈顶元素和宽度乘积(计算弹出矩形的最大面积)
top--;
}
top++;
zhan[top]=a[i];
w[top]=kuan+1;
}
}
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
scanf("%lld",&n);
while(n)
{
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
work();
printf("%lld\n",ans);
scanf("%lld",&n);
}
return 0;
}
这就是著名的单调栈算法,借助单调性处理问题的思想在于及时排除不可能的选项,保持策略集合的高度有效性和秩序性,从而为我们做出策略提供更多的条件和可能方法。
——《算法进阶指南》
0x12 队列
c++ STL queue的用法详见
·小组队列
这道题是一道很简单的模拟题
我们建立t+1个队列,其中\(Q_0\)存储小组的顺序,\(Q_i\)存储编号为\(i\)的小组的组内顺序,每加入一个数,我们就把它插到其小组的最后;如果小组队列为空,还要把小组编号插入\(Q_0\)最后。
实现代码:
#include<cmath>
#include<queue>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int T=1000010;
int tong[T]={0};
int main()
{
int t,l,w=0;
string p;
scanf("%d",&t);
while(t)
{
w++;
queue<int> qu[1010];
int x;
for(int i=1;i<=t;i++)
{
scanf("%d",&l);//长度
for(int j=1;j<=l;j++)
{
scanf("%d",&x);
tong[x]=i;//桶,储存每个编号的小组
}
}
printf("Scenario #%d\n",w);
cin>>p;
while(p!="STOP")
{
if(p=="ENQUEUE")
{
scanf("%d",&x);
if(qu[tong[x]].empty())
qu[0].push(tong[x]);
qu[tong[x]].push(x);
}
else
{
printf("%d\n",qu[qu[0].front()].front());
qu[qu[0].front()].pop();
if(qu[qu[0].front()].empty())
qu[0].pop();
}
cin>>p;
}
printf("\n");
scanf("%d",&t);
}
return 0;
}
·蚯蚓
NOIP2016提高组
老早就想吐槽了,为甚么蛐蛐国会蚯蚓成灾啊!!


