台大林轩田老师《机器学习技法》课程笔记2:Combining Predictive Features: Aggregation Models
前言:这一块内容主要介绍集成模型。个人觉得其中Bagging、Adaboost和RandomForest讲解的很精彩,受益匪浅;但决策树、GBDT部分讲解不如西瓜书和蓝皮书,所以这两块内容按照自己的理解整理而成,仅供参考。
2 Combining Predictive Features: Aggregation Models
2.1 Blending and Bagging
上一块内容主要介绍Kernel Models及其应用,现在将介绍Aggregation Models,即如何将不同的hypothesis和features结合起来,让模型更好。本节课将介绍其中的两个方法,一个是Blending,一个是Bagging。
理解:集成方法中,各个\(g_t(x)\)都是对x的一种转换(普遍成立),然后以平均、线性、非线性方式组合。
2.1.1 Motivation of Aggregation
首先举个例子来说明为什么要使用Aggregation。假如你有T个朋友,每个朋友向你预测推荐明天某支股票会涨还是会跌,对应的建议分别是\(g_1,g_2,\cdots,g_T\),那么你该选择哪个朋友的建议呢?即最终选择对股票预测的\(g_t(x)\)是什么样的?

将刚刚举的例子的四种方法用数学化的语言表示出来:

为什么Aggregation能work得更好?有两个原因(feature transform和regularization的效果):一是aggregation提高了预测模型的power,起到了特征转换(feature transform)的效果;二是对各种效果较好的可能性进行组合,得到更中庸、更稳定的结果,起到了正则化(regularization)的效果。通常单一模型只能倾向于feature transform和regularization之一,在两者之间做个权衡。但是aggregation却能将feature transform和regularization各自的优势结合起来,好比把油门和刹车都控制得很好,从而得到不错的预测模型。
2.1.2 Blending
对于已经选择的性能较好的一些矩\(g_t\),将它们进行整合、合并,来得到最佳的预测模型的过程称为blending。Blending通常分为三种情况:Uniform Blending,Linear Blending和Any Blending。其中,uniform blending采用最简单的“一人一票”的方法,linear blending和any blending都采用标准的two-level learning方法,类似于特征转换的操作,来得到不同\(g_t\)的线性组合或非线性组合。
1) Uniform Blending
Uniform blending种类:

uniform blending for regression中,计算\(g_t\)的平均值可能比单一的\(g_t\)更稳定,更准确。下面进行简单的推导和证明。

上述等式中左边表示演算法误差的期望值;右边第二项表示不同\(g_t\)的平均误差共识,用偏差bias表示;右边第一项表示不同\(g_t\)与共识的差距是多少,反映\(g_t\)之间的偏差,用方差variance表示。也就是说,一个演算法的平均表现可以被拆成两项,一个是所有\(g_t\)的共识,一个是不同\(g_t\)之间的差距是多少,即bias和variance。而uniform blending的操作时求平均的过程,这样就削减弱化了上式第一项variance的值,从而演算法的表现就更好了,能得到更加稳定的表现。
2) Linear and Any Blending
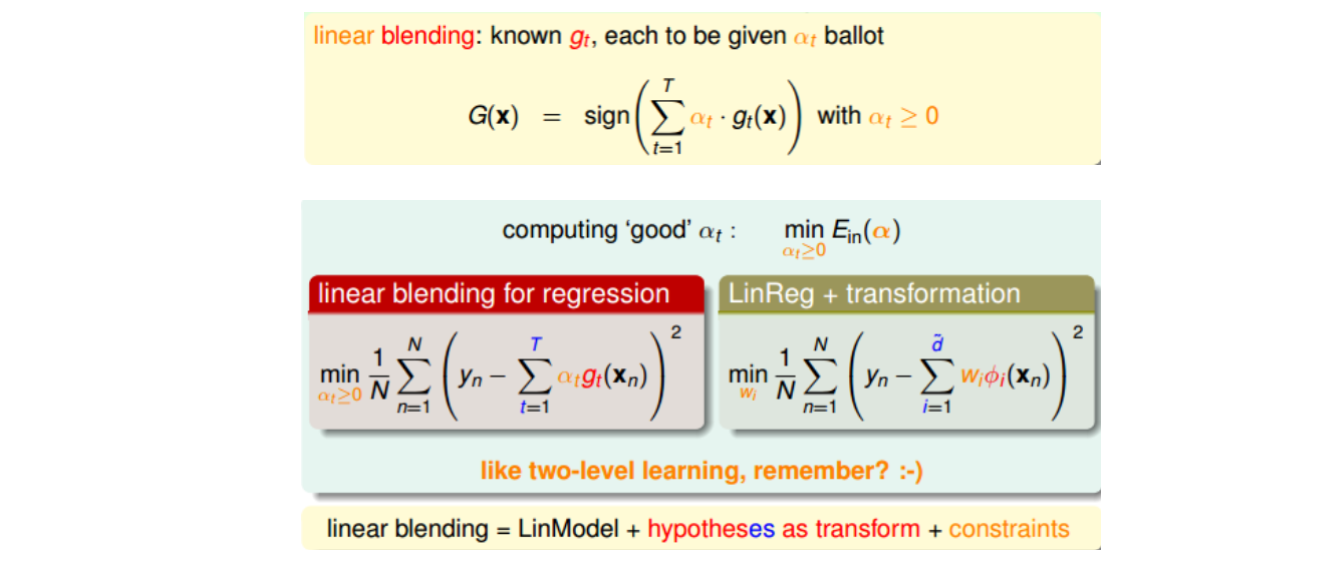
这种求解\(\alpha_t\)的方法就像是使用two-level learning,类似于我们之前介绍的probabilistic SVM。这里,我们先计算\(g_t(x_n)\),再进行linear regression得到\(\alpha_t\)值。总的来说,linear blending由三个部分组成:LinModel,hypotheses as transform,constraints。其中值得注意的一点就是,计算过程中可以把\(g_t\)当成feature transform,求解过程就跟之前没有什么不同,除了\(\alpha\geq0\)的条件限制。不过\(\alpha\geq0\)的条件限制也可以省掉。
除了linear blending之外,还可以使用任意形式的blending。linear blending中,G(t)是g(t)的线性组合;any blending中,G(t)可以是g(t)的任何函数形式(非线性)。这种形式的blending也叫做Stacking。
2.1.3 Bagging(Bootstrap Aggregation)
blending关注的是将已经得到的矩\(g_t\)进行aggregate的操作。具体的方法有uniform,non-uniforn和conditional。那如何得到不同的\(g_t\)?方法有:选取不同模型H;可以设置不同的参数,例如\(\eta\)、迭代次数n等;可以由算法的随机性得到,例如PLA、随机种子等;可以选择不同的数据样本等。这些方法都可能得到不同的\(g_t\)。
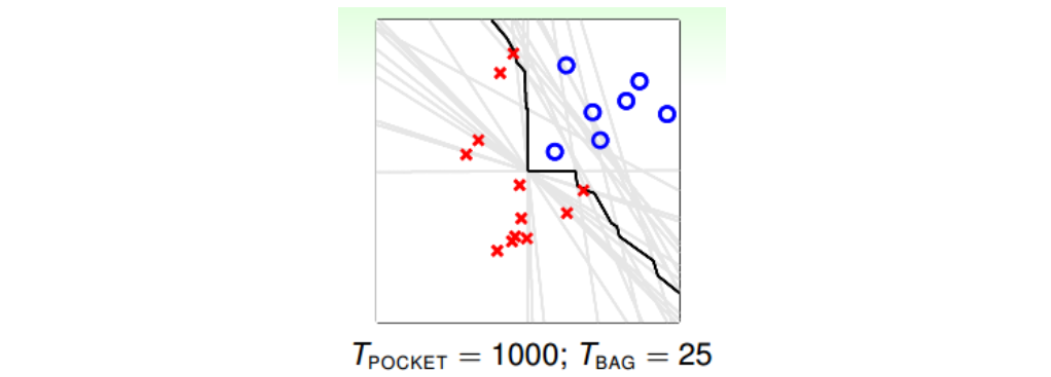
这里采用Bootstrapping的方式,利用已有的一份数据集来构造出不同的\(g_t\)。做法是在N笔资料中,有放回的抽取一个样本,重复N次,即可得到一个新的N笔资料。利用bootstrap进行aggragation的操作就被称为bagging。值得注意的是,只有当演算法对数据样本分布比较敏感的情况下,才有比较好的表现。
2.2 Adaptive Boosting(AdaBoost)
上一节课介绍了blending方法,是将已存在的所有\(g_t\)结合起来,可以是uniformly,linearly,或者non-linearly组合形式。然后,在没有那么多\(g_t\)的情况下,可以使用bootstrap方式,从已有数据集中得到新的类似的数据集,从而得到不同的\(g_t\)。这种做法称为bagging。本节课将继续从这些概念出发,介绍一种新的演算法AdaBoost。
2.2.1 AdaBoost算法的两个引子
引子一:小学生认识苹果的案例
比如说,老师展示一些图片,让6岁孩子们通过观察,判断其中哪些图片的内容是苹果。从判断的过程中推导如何解决二元分类问题的方法。
首先,有学生说苹果应该是圆的。根据他的判断,图片中大部分苹果都能被识别出来,但也有些错误。于是老师将这些错误的样本画上重点,让学生们再一次辨认。经过几轮讨论之后,苹果被定义为:圆的,红色的,也可能是绿色的,上面有梗。这种做法就是AdaBoost思想的原型:不同的学生代表不同的hypotheses \(g_t\);最终得到的苹果总体定义就代表hypothesis G;而老师就代表演算法A,指导学生的注意力集中到关键的例子中(错误样本),从而得到更好的苹果定义。
引子二:通过重定义权重来控制各\(g_t\)之间的多样性
上一节课中介绍的bootstrapping方法,换个角度来看,可以写成下图形式。参数u相当于是权重因子,当\(\hat{D}_t\)中第i个样本出现的次数越多的时候,那么对应的\(u_i\)越大,表示在error function中对该样本的惩罚越多。所以从另外一个角度来看bagging,它其实就是通过bootstrap的方式,来得到这些\(u_i\)值,作为犯错样本的权重因子,再用base algorithn最小化包含\(u_i\)的error function,得到不同的\(g_t\)。这个error function被称为bootstrap-weighted error。

上节课中说,\(g_t\)越不一样,其aggregation的效果越好,即每个人的意见越不相同,越能运用集体的智慧,得到好的预测模型。所以为了使各\(g_t\)差异更大,可以调节各\(u_i\)的值。思想如下:
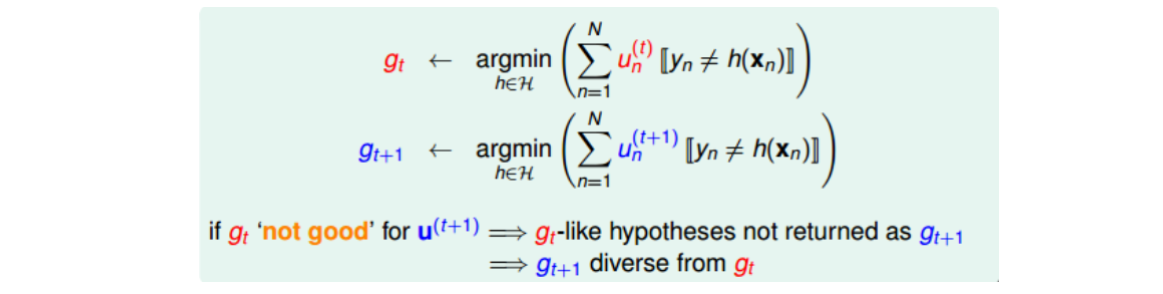
如上所示,\(g_t\)是由\(u_n^{(t)}\)得到的,\(g_{t+1}\)是由\(u_n^{(t+1)}\)得到的。如果\(g_t\)这个模型在使用\(u_n^{(t+1)}\)的时候得到的error很大,即预测效果非常不好,那就表示由\(u_n^{(t+1)}\)计算的\(g_{t+1}\)会与\(g_t\)有很大不同。故可以调整\(u_n^{(t+1)}\),使得\(g_t\)在\(u_n^{(t+1)}\)表现最差(和瞎猜没区别),即err为0.5。

2.2.2 Adaptive Boosting Algorithm

AdaBoost算法核心有三部分:base learning algorithm A,re-weighting factor \(\diamond t\)(书写上用\(s_t\)替代)和linear aggregation \(\alpha_t\)。其中:
- A通常是个比较弱的算法(\(\epsilon_t \leq \epsilon \leq \frac{1}{2}\),比乱猜好就行)。
- 缩放因子\(s_t = \sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\),其物理含义是,如果\(\epsilon_t < \frac{1}{2}\),则相当于,针对上一个模型分类结果,增大错误样本的权重,减小正确样本的权重。若\(\epsilon_t \geq \frac{1}{2}\),做相反推论同样成立。
- \(\alpha_t\)是将一系列弱模型线性组合起来的系数,算法算法在求\(g_{t+1}\)的时候,顺便将\(g_t\)的线性组合系数\(\alpha_t\)也求得了,故又称Linear Aggregation on the Fly算法。\(\alpha_t = ln(s_t)\)的物理意义是,当\(\epsilon_t=\frac{1}{2}\)时,error很大,跟瞎猜没区别,即此\(g_t\)对G没有什么贡献,权重应该设为零;当\(\epsilon_t\)趋近于0时,表示该\(g_t\)预测非常准,权重应设置的很大;当\(\epsilon_t\)趋近于1时,反着推论也成立。
20190806疑问待解:为啥在第二步中求\(\epsilon_t\)时候,还要用\(u_n^{(t)}\),照理说缩放因子和第三步中的\(\alpha_t\)都应该用原始的数据集D上的误差来求?另外,bootstrap的方式是否改变了数据的分布?如果改变了,是否学的模型就?(20190812附注想法:第一个问题,确实要用\(u_n^{(t)}\)的,因为要使下一个模型和上一个模型差别最大,就应该更多地用上一个模型出错的样本去训练。第二个问题,肯定会改变数据的分布的,比如在Adaboost中,每次都会根据上一个模型的表现刻意地调整下一轮的权重,但由于还是那些数据,所以是强调性地体现了总体分布的某些方面,正是这些分布的差异,让各个模型相对于目标函数的方差更大,由此得到的集成模型就更加鲁棒。)
从VC bound角度来看,AdaBoost算法理论上满足:

上式中,\(E_{out}(G)\)的上界由两部分组成,一项是\(E_{in}(G)\),另一项是模型复杂度\(O(*)\),可以证明G的\(d_{vc}\)服从\(O(d_{vc}(H)\cdot Tlog\ T)\)。对这个VC bound中的第一项\(E_{in}(G)\)来说,有一个很好的性质:如果满足\(\epsilon_t\leq \epsilon \leq \frac{1}{2}\),则经过\(T=O(log\ N)\)次迭代之后,\(E_{in}(G)\)能减小到等于零的程度。而当N很大的时候,其中第二项也能变得很小,则整个\(E_{out}(G)\)就能被限定在一个有限的上界中。
2.3 Decision Tree
Decision Tree可以理解成,根据条件对特征空间的一个划分。在各个划分单元内,以各自最大的类别作为标记类,或者以单元内值的平均作为该单元的值。(这一点类似KNN?)
从aggregation的角度而言,三种聚合方式应用如下。其中决策树是有条件的聚合方式,即一系列条件下才能到达叶节点。

个人感觉本节讲的不太清晰,故自行采用西瓜书和统计学习方法里面的结构。框架为:
- 基本算法;
- 最优划分属性选择;
- 剪枝;
- 连续与缺失值处理,多变量决策树;
2.3.1 基本算法
输入:D,A
输出:决策树T(D, A)
过程:函数TreeGenerate(D, A)
1).生成结点node;
2).if D中样本全属于同一类别C then:
——将node标记为C类叶节点,返回;
3).if A为空集,或D中样本在A中所有属性上取值均相同 then:
——将node标记为叶节点,类别为D中样本数最多的类,返回;
4).从A中选出一个最优划分属性\(a_*\);
5).for \(a_*\)的每一个取值\(a_*^V\), do:
——令\(D_V\)表示D在\(a_*\)上取值为\(a_*^V\)的样本子集;
——if \(D_V\)为空,则生成并标记成叶节点,类别为父节点D中样本最多的类,返回;
——else TreeGenerate(\(D_V\), \(A-a_*\));
——end if
end for
算法说明:
- 符号说明:D表示数据集,A表示属性集,a表示A中某一属性,\(a_*^V\)表示属性\(a_*\)的一个取值;
- 文档无法缩进,故用横线表缩进;
- 最优属性的划分采用的指标:信息增益(ID3算法)、信息增益率(C4.5算法)、基尼指数(CART算法);
- 通常会在第四步之后判定指标是否小于阈值,若是则可以直接打结。
2.3.2 三种寻找最优划分属性的指标
符号说明:D表示数据集,\(|D|\)表示样本容量。设有K个类\(C_k\),\(|C_k|\)表示属于类\(C_k\)的样本个数,\(\sum\limits_{k=1}^{K}|C_k|=|D|\)。设特征A有n个不同的取值,根据各取值将D划分为n个子集\(D_i\)。子集\(D_i\)中属于类\(C_k\)的样本的集合为\(D_{ik}\)。
注意:上一小节算法过程中A表示属性集,此处A表示某一个属性,\(A_i\)表示特征A的一个取值。
1.信息增益
集合D的经验熵:
特征A给定条件下D的经验条件熵:
特征A对D的信息增益:
2.信息增益率
D关于特征A的取值的熵:
特征A对D的信息增益率:
3.基尼指数
集合D的基尼指数(连续两次抽样类别不一致的概率,表征D的不纯度):
集合D在特征A条件下的基尼指数:
2.3.3 剪枝
目的是为了防止过拟合。分为预剪枝和后剪枝。
预剪枝是指,在决策树生成的过程中,对每个结点进行划分之前进行估计,若划分不能带来泛化性能的提升,则停止该结点的划分,并将其标记为叶节点。后剪枝是指,在决策树生成之后,自下而上地对每个非叶节点进行考察,若将该结点替换成叶节点之后能带来泛化性能的提升,则将其替换成叶节点。
2.3.4 连续与缺失值处理
对于连续值的处理,通常采用二分法。对该属性值进行划分,小于该值的为一类,其余的为另一类;对n个值而言,可以有n-1个划分点。
对于缺失值的处理(讨论构建决策树时情况),需要解决两个问题:一是如何在属性值a缺失的情况下选择划分属性?二是在给定划分属性a的情况下,若样本的该属性值缺失,如何将样本划分到下一个结点上?采用的方法是,先将该属性值正常的样本挑出来,计算这些样本中属性a带来的信息增益,然后乘以这些样本所占比例。针对第二个问题,可以将同一个样本以不同的权重同时划分到不同的子结点中去。
对于预测时样本属性值缺失的问题,以后再补充。
多变量决策树是指,基本的DT只能对单一属性进行划分(二维中只能横着切或竖着切),而多变量决策树在每一次的属性划分时,可以斜着切,即对属性的组合进行考察。
2.4 Random Forest
2.4.1 Random Forest Algorithm
基本的RF是将Bagging和DT结合起来。

Decision Tree具有variance比较大的特点。这是因为Decision Tree每次切割的方式不同,而且分支包含的样本数在逐渐减少,所以它对不同的资料D会比较敏感一些,variance比较大。而Bagging是通过不同的数据集来构造基学习器(所以偏好对数据扰动比较敏感的学习器),然后将所有\(g_t\) uniform结合起来,起到了求平均的作用,从而降低variance。故两者优势互补。
Random Forest算法的优点主要有三个。第一,不同决策树可以由不同主机并行训练生成,效率很高;第二,随机森林算法继承了CART的优点;第三,将所有的决策树通过bagging的形式结合起来,避免了单个决策树造成过拟合的问题。
以上是基本的Random Forest算法。为了得到更具有多样性的决策树,除了数据扰动外,还可以增加属性扰动和属性组合。
- 属性扰动是,假设原来样本维度是d,则只选择其中的d’(d’小于d)个维度来建立决策树结构。这类似是一种从d维到d’维的特征转换,相当于是从高维到低维的投影,也就是说d’维z空间其实就是d维x空间的一个随机子空间(subspace)。Random Forest算法的作者建议在构建CART每个分支b(x)的时候,都可以重新选择子特征来训练,从而得到更具有多样性的决策树。
- 属性组合就是前面构建决策树时采用多变量决策树(前者随机子空间是其一种特例)。

2.4.2 Out-Of-Bag Estimate(包外估计)
Bagging中的bootstrap方法除了能提供不同的数据集(且分布不变)来构造基学习器,还具有自带验证集的功效。
Bagging是通过bootstrap得到新的样本集D’来训练基学习器\(g_t\),原D中大约有三分之一的样本没有被选中(因为\((1-\frac{1}{N})^N \approx \frac{1}{e}\))。对于各\(g_t\)来说,这些没有被选中的样本称为out-of-bag(OOB) example。比如下图中红色* 。
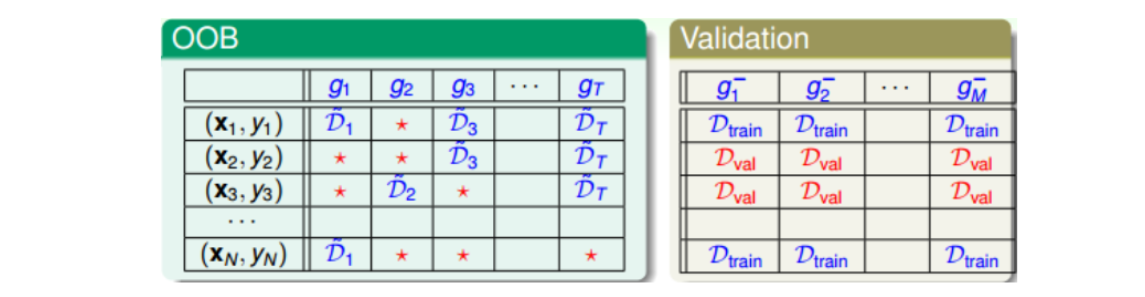
在Validation中,通常会选出固定比例的验证集来评估各自的\(g_m^-\),OOB样本与之类似,也可以作为验证样本。但与之不同的是,Validation是用验证集逐个评估单一的\(g_m^-\),而OOB是要评估由许多\(g_t\)组合成的G。
方法是,针对每一个样本\((x_n,y_n)\),看看它是哪些\(g_t\)的OOB资料,然后计算其在这些\(g_t\)上的平均表现,记为\(G_n^-(x)\),比如上图中样本\((x_N,y_N)\)在\(G_N^-(x)\)上表现为\(G_N^-(x) = average(g_2, g_3, g_T)\)。与Leave-One-Out Cross Validation类似,每次只对一个样本进行验证,最后计算所有样本的平均表现:\(E_{oob}(G) =\frac{1}{N} \sum\limits_{n=1}^{N}err(y_n, G_n^-(x))\)。我们把\(E_{oob}\)称为bagging或者Random Forest的self-validation,估算的就是G的表现好坏。随机森林算法中,self-validation在衡量G的表现上通常相当准确。
另外,self-validation相比于validation来说还有一个优点就是它不需要重复训练。它在调整随机森林算法相关系数并得到最小的\(E_{oob}\)之后,就完成了整个模型的建立,无需像Validation那样重新训练模型。
2.4.3 Feature Selection
特征选择的目的是为了去除冗余特征和无关特征。好处有三:1.提高效率,特征越少,模型越简单;
2.正则化,防止特征过多出现过拟合;3.去除无关特征,保留相关性大的特征,解释性强。缺陷也有三:1.筛选特征的计算量较大;2.不同特征组合,也容易发生过拟合;3.容易选到无关特征,导致解释性差。
对多维特征进行筛选的方法是,通过计算出每个特征的重要性(即权重),然后再根据重要性的排序进行选择即可。这种方法在线性模型中比较容易计算,因为线性模型的score是由每个特征经过加权求和而得到的,而加权系数的绝对值\(|w_i|\)正好代表了对应特征\(x_i\)的重要性为多少。但对于非线性模型来说,因为不同特征可能是非线性交叉在一起的,所以计算每个特征的重要性就变得比较复杂和困难。但是,RF是个例外。
RF中,特征选择的核心思想是random test。random test的做法是对于某个特征,如果用另外一个随机值替代它之后的表现比之前更差,则表明该特征比较重要,反之则不重要。即通过比较某特征被随机值替代前后的表现,就能推断出该特征的权重和重要性。
random test中选取随机值通常有两种方法:一是使用uniform或者gaussian抽取随机值替换原特征;二是通过permutation的方式将原来的所有N个样本的第i个特征值重新打乱分布(相当于重新洗牌)。比较而言,第二种方法更加科学(第一种无法保证分布相同,且容易引入噪声),保证了特征替代值与原特征的分布是近似的(只是重新洗牌而已)。这种方法叫做permutation test(随机排序测试),即在计算第i个特征的重要性的时候,将N个样本的第i个特征重新洗牌,然后比较模型在D和\(D^{(p)}\)表现的差异性。如果差异很大,则表明第i个特征是重要的。

知道了permutation test的原理后,接下来要考虑替换前后的表现。显然RF的performance可以用\(E_{oob}(G)\)来衡量。但是,对于N个样本的第i个特征值重新洗牌重置的\(D^{(p)}\),要对它进行重新训练,而且每个特征都要重复训练,然后再与原D的表现进行比较,过程非常繁琐。为了简化运算,RF的作者提出了一种方法,就是把permutation的操作从原来的training上移到了OOB validation上去,记为\(E_{oob}(G^{(p)})\rightarrow E_{oob}^{(p)}(G)\)。即在训练的时候仍然使用D,但是在OOB验证的时候,将所有的OOB样本的第i个特征重新洗牌,验证G的表现。这种做法大大简化了计算复杂度,在RF的feature selection中应用广泛。

2.5 GBDT
注:这一节觉得讲解不如蓝皮书《统计学习方法》,因此这一节内容是在蓝皮书基础上针对性解释几个困惑点。
GBDT是在Adaboost基础上,把Adaboost的指数损失函数换成一般的可导损失函数,直接用损失函数的负梯度作为残差的近似值,然后用下一棵树来拟合这个残差,使得损失函数逐渐降低。GBDT的主要内容都包含在名字里,Gradient Descent + Boosting + DT。
- Boosting:加法模型 + 前向分布算法;
- Gradient Descent:针对目标函数的梯度下降;
- DT:DT作为基学习器
为啥要用损失函数的负梯度?
20191125注:之前一直对GBDT似懂非懂,即《统计学习方法》中算法8.4(梯度提升算法),不明白为啥说要用损失函数的负梯度来拟合一个回归树。这两天终于理清楚这个问题了。主要总结如下:
- 在经常用的梯度下降法中,负梯度方向是下降最快的方向,这个是由一阶泰勒展开式推导得到的。(牛顿法可由二阶泰勒展开式得到。)
- 梯度提升方法是一种加法模型,采用前向分布算法求取各个基学习器的参数。之所以不需要求各个基学习器的权重,是因为基学习器都是回归器,权重可以内化到学习器的内部。即迭代m步之后的模型为 \(f_m(x) = f_{m-1}(x) + b_m(x)\)。
- 梯度提升方法和其他算法一样,主要目标是想办法降低损失函数。
- 算法8.4中泛化的损失函数(可能是平方损失,也可能是huber损失或其他损失)是个复合函数,各个样本点 \([x_1, x_2, ..., x_N]^T\) 经过模型 \(f\) 转换之后得到一个函数向量 \([f(x_1), f(x_2), ..., f(x_N)]^T\),这个函数向量再连同 \([y_1, y_2, ..., y_N]^T\) 构成了损失函数。随着模型 \(f\) 的不断变化,函数向量的输出值也不断变化。
- 把函数向量 \([f(x_1), f(x_2), ..., f(x_N)]^T\) 当做损失函数的自变量,则梯度提升法的关键点就转化成:假设自变量 \([f(x_1), f(x_2), ..., f(x_N)]^T\) 已经走了 \(m-1\) 步,那基于当前位置,下一步该怎么走,才能让损失函数进一步下降呢?(即已知上一次迭代后的模型 \(f_{m-1}\),下一步该加上一个什么样的基学习器 \(b_m\) 来更新 \([f(x_1), f(x_2), ..., f(x_N)]^T\),才能让损失函数进一步下降呢?)答案是和普通的梯度下降法一样,就是损失函数在当前位置关于自变量的负梯度方向。(此处可以用损失函数的一阶泰勒展开来说明。)
- 换句话说,\([b_m(x_1), b_m(x_2),... b_m(x_N)]\) 就相当于普通梯度下降法中即将要走的那一小步(即\(- \eta \nabla f\)),因为回归学习器可以内化权重,所以连步长 \(\eta\) 也省掉了。
- 附上两篇参考文章:(梯度下降法推导);
(梯度提升树推导).
关于蓝皮书算法8.4(梯度提升算法)的理解
20191126注:昨天看到有人说蓝皮书里面有个问题,就是算法8.4里面GBDT的负梯度没有用步长。我仔细想了想,觉得这个算法里面确实有两个疑问:
- 第一个问题:直接用损失函数的负梯度作为下一棵树的拟合目标,真的可以吗?参考文章里面说回归树本身可以内化这个步长,因此可以把步长省掉,因为回归就是要拟合一个实数。这个说法乍一听很有道理,但是仔细推敲起来却貌似有些问题。比如有5个样本\([(x_1,1),(x_2,2),(x_3,3),(x_4,4),(x_5,5)]\),假设GBDT里面损失函数用的是4倍的平方损失,即 \(2 \times (y_i - f)^2\),那么算法是这样运行的:\(f_0(x)\) 先初始化成[3,3,3,3,3],则损失函数的负梯度为 \(4 \times [-2,-1,0,1,2]\),即第一棵树的拟合目标是 \([(x_1,-8),(x_2,-4),(x_3,0),(x_4,4),(x_5,8)]\)。这是个很大的问题,因为正常算法(比如算法8.3)中下一棵树拟合的应该是残差\([-2,-1,0,1,2]\),这里却是残差的4倍。对于决策树而言,各样本特征不变,标签值虽然变了,但分布没变,所以两种算法学到的第一棵回归树结构肯定是一样的,只是叶子节点的输出差了4倍。假设第一棵树只有两个叶子节点,落在左叶子里的是 \([x_1,x_2]\) 两个样本,落在右叶子里的是 \([x_3,x_4,x_5]\) 三个样本。那么,现在把样本 \(x_2\) 喂给第一棵树,本来第一棵树应该输出-1.5,但是现在却输出-6,这简直是开玩笑嘛!
- 第二个问题:算法8.4中第一步为啥要这样初始化 \(f_0\),为啥不是初始化成0?
又想了很久,觉得有些收获,分享如下。请各位大神路过时不吝指教。
- 针对问题1,算法8.4其实是对的,核心就在于2c这一步。我举的那个例子实际上有一个隐含的前提,即回归树上叶子节点的输出值是落在这个叶子上的样本的平均值(CART回归树就是这么输出的),但GBDT中却不是。在算法8.4的2c这一步中,叶子的输出值并非直接取平均,而是最小化这个叶子的整体损失。即那个例子中第一棵树虽然拟合目标是 \([(x_1,-8),(x_2,-4),(x_3,0),(x_4,4),(x_5,8)]\),但最后每一个叶子的输出值却是真实残差的平均值,也就是说,2c个式子剔除了负梯度的倍数带来的影响,使得这棵树拟合的就是真实的残差。延伸开来就可以明白,CART回归树的叶子输出值之所以敢直接取平均值,是因为它默认使用平方损失,本质上还是2c个式子。
- 针对问题2,我感觉这个初始化带来的影响就是让下一棵树的拟合目标去均值化,比如上面的例子中如果按平方损失,则第一棵树的拟合目标就变成了\([(x_1,-2),(x_2,-1),(x_3,0),(x_4,1),(x_5,2)]\)。虽然去均值化对决策树本身的构建没啥影响,但这个 \(f_0\) 却有些作用,因为它毕竟也是一棵树,也参与了总模型的拟合过程。当然把它初始化为0也是没问题的,只是它的拟合作用被后面的模型承担而已。
想通了问题2,就可以看出蓝皮书中算法8.4中最后一行(3)实际上有点问题,即总模型应该包括 \(f_0\) 的,所以下标m应该是从0开始的。当然编程时候肯定是没问题的,因为2d这一步已经把 \(f_0\)包含进去了。
注意:
- 决策树不关心具体标签值是多少,而只关心各个样本的特征和标签值的分布;
- 用负梯度来估计残差肯定不准确,但是GBDT中2c可以对冲掉这一偏差;
- GBDT不需要步长,但对于其他GB方法就不一定。

