台大林轩田老师《机器学习基石》课程笔记4:How Can Machines Learn Better?
4 How Can Machines Learn Better?
4.1 Hazard of Overfitting
4.1.1 What is Overfitting?
过拟合定义:学习时选择的模型复杂度过高,导致这一模型的训练误差很小,但预测误差却很大的现象。(自行脑补\(E_{in}、E_{out}\)随模型复杂度变化的学习曲线。)
过拟合原因:VC Dimension太大、Noise、数据量N不够。即VC Dimension、Noise、N这三个因素是影响过拟合现象的关键。
原因1:VC Dimension太大;
- \(E_{in}、E_{out}\)随模型复杂度变化的学习曲线。
原因2:N不足;(思考:\(d_{VC}\)过大导致的过拟合,本质上也是数据不足?)
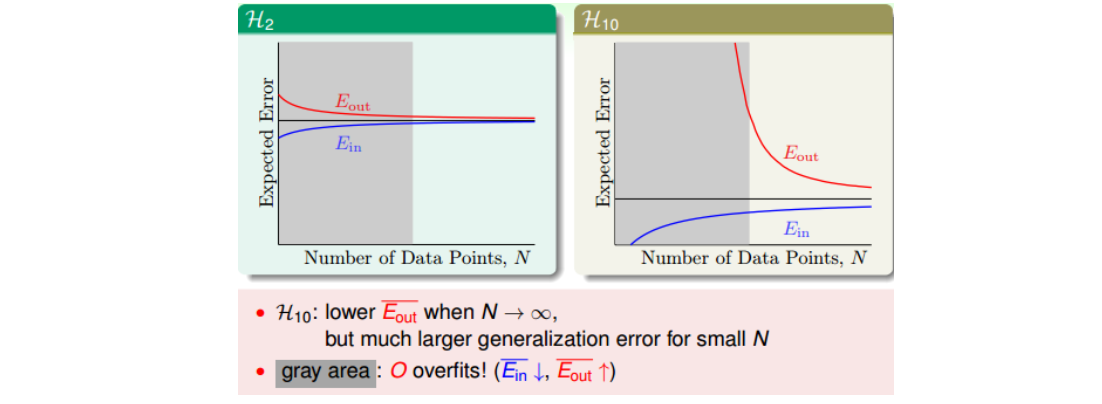
- 课件实验中,目标函数f为10次和50次多项式,分别采用2次和10次的模型去学习,结果表明10次的模型均发生了过拟合,与直觉相悖。
- 原因在于,在learning curve中,\(E_{in}\)和\(E_{out}\)可表示如下。数据量N不大时对应于下图中的灰色区域。虽然H(10)的期望误差更小,但在N不足时,\(E_{out}\)仍然会很大。(思考:1.每个复杂度都对应一个合适的N范围,若N不足,即便g和f的复杂度一样,也会导致过拟合。另外,当复杂度较高时,会发生维度灾难。2.是否可根据现有的N反推出最大的\(d_{VC}\))
原因3:Noise;
- Stochastic Noise:服从高斯分布的噪声;
- Deterministic Noise:由于目标函数f的\(d_{VC}\)高于模型的\(d_{VC}\),导致再好的hypothesis都会跟它有一些差距,我们把这种差距称之为deterministic noise。deterministic noise与stochastic noise不同,但是效果一样。其实deterministic noise类似于一个伪随机数发生器,它不会产生真正的随机数,而只产生伪随机数。

4.1.2 Dealing with Overfitting

- start from simple model
- data cleaning/pruning:对训练数据集里label明显错误的样本进行修正(data cleaning),或者对错误的样本看成是noise,进行剔除(data pruning)。data cleaning/pruning关键在于如何准确寻找label错误的点或者是noise的点,而且如果这些点相比训练样本N很小的话,这种处理效果不太明显。
- data hinting:针对N不够大的情况,如果没有办法获得更多的训练集,那么data hinting就可以对已知的样本进行简单的处理、变换,从而获得更多的样本。举个例子,数字分类问题,可以对已知的数字图片进行轻微的平移或者旋转,从而让N丰富起来,达到扩大训练集的目的。这种额外获得的例子称之为virtual examples。但是要注意一点的就是,新获取的virtual examples可能不再是iid某个distribution。所以新构建的virtual examples要尽量合理,且是独立同分布的。
- regularization
- validataion
注:Ng课程中提到,利用训练测试误差随N变化的学习曲线来判断是欠拟合还是过拟合,从而决定是否要增加数据量来减轻过拟合。
4.2 Regularization
L2正则化两种理解方式:
- 课件中通过Lagrange multiplier,解决有条件的最佳化问题;
- Ng视频课中理解方式(代价函数修正)。
带正则化项的两种解法(见Ng课件):梯度下降法;正规方程法。
注意:梯度下降法中正则化项又称为weight-decay regularization;带正则化的正规方程法又称为ridge regression(统计学上),可以看成是linear regression的进阶版。
根据VC理论,加上正则化项之后,模型的VC维度(\(d_{EFF}(H,A)\))小于正常模型的VC维度。因为受regularized的影响,限定了w只取一小部分。这些与实际情况是相符的,比如对多项式拟合模型,当\(\lambda=0\),所有的w都给予考虑,相应的\(d_{VC}\)很大,容易发生过拟合。当\(\lambda > 0\)且越来越大时,很多w将被舍弃,\(d_{EFF}(H,A)\)减小,拟合曲线越来越平滑,容易发生欠拟合。
对于通用的Regularizers,即\(\Omega(w)\),一般我们会朝着目标函数的方向进行选取。有三种方式:target-dependent;plausible;friendly。(与之前的error measure选取原则类似。)比如Noise越大,\(\lambda\)通常越大。

4.3 Validation
直接使用\(E_{in}\)、\(E_{test}\)都是不太好的.
4.3.1 Cross Validation
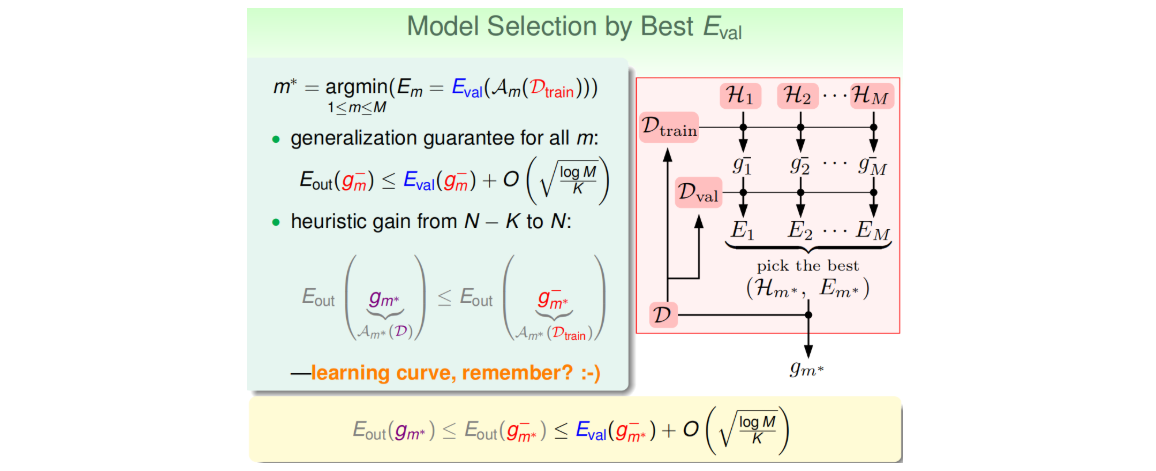
机器学习模型建立的过程中有许多选择,比如算法的选择、学习率、正则化参数等,会组合形成多个模型。模型选择通常可以按照以下流程:
- 1.从D中随机抽取一部分数据作为验证集(保证iid;通常为D的20%;划分验证集,通常并不会增加整体时间复杂度,反而会减少,因为\(D_{train}\)减少了);
- 2.将各个模型(假设空间)在训练集上跑一遍,挑出各个模型的\(g^-_m\)(因为D被挖掉一块,所以上标用-);
- 3.用验证集找出最小的\(E_{val}\),对应的模型(假设空间)序号记为\(m^*\)(思考:这两步主要是为了找出最合适的\(d_{VC}\),\(E_{val}\)最小的那个模型\(E_{out}\)与\(E_{in}\)最接近,即对应的模型泛化性能最好);
- 4.将找到的这个模型(第\(m^*\)个)再重新在整个D上跑一遍,找到\(g_{m^*}\)(注意并非直接采用\(E_{val}\)最小的\(g^-_m\),其效果不如这种方法。该案例见课件。)。
4.3.2 Leave-One-Out Cross Validation
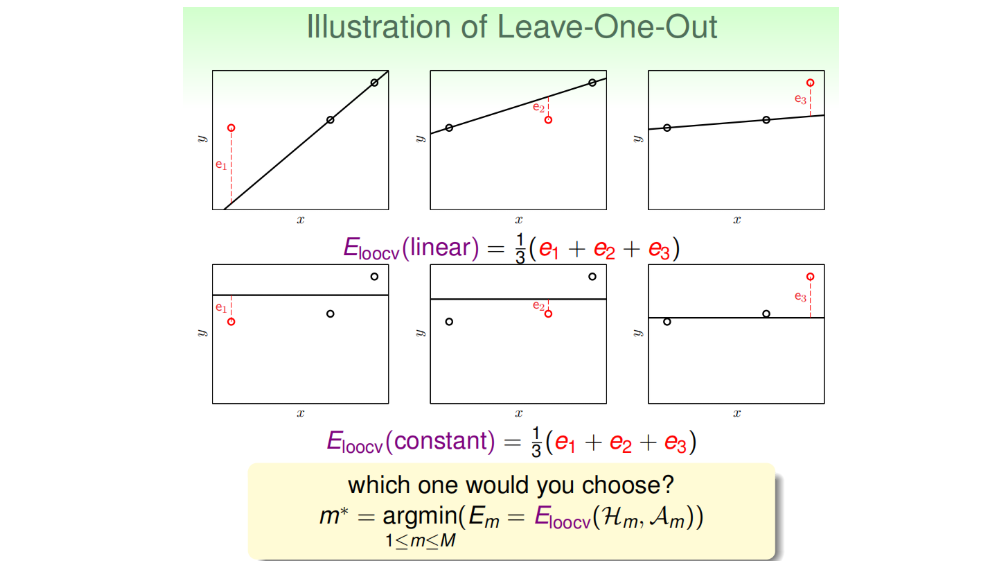
考虑一个极端的例子,k=1,即验证集大小为1,即每次只用一组数据对\(g_m\)进行验证。这样做的优点是\(g_m^-\approx g_m\),但是\(E_{val}\)与\(E_{out}\)可能相差很大。为了避免\(E_{val}\)与\(E_{out}\)相差很大,每次从D中取一组作为验证集,直到所有样本都作过验证集,共计算N次,最后对验证误差求平均,得到\(E_{loocv}(H,A)\),这种方法称之为留一法交叉验证,求平均的目的是为了让\(E_{loocv}(H,A)\)尽可能地接近\(E_{out}(g)\)。
该方法的两个问题:
- 计算量,假设N=1000,那么就需要计算1000次的\(E_{loocv}\),再计算其平均值。当N很大的时候,计算量是巨大的,很耗费时间。
- 稳定性,例如对于二分类问题,取值只有0和1两种,预测本身存在不稳定的因素,那么对所有的\(E_{loocv}\)计算平均值可能会带来很大的数值跳动,稳定性不好。所以,这两个因素决定了Leave-One-Out方法在实际中并不常用。
4.3.3 K-fold Cross Validation
针对Leave-One-Out的缺点,对其作出改进。Leave-One-Out是将N个数据分成N分,那么改进措施是将N个数据分成K份(常常K=10),计算过程与Leave-One-Out相似。这样可以减少总的计算量,又能进行交叉验证。实际中经常用此法,平均预测误差即可作为该模型的性能指标。
4.4 Three Learning Principles
奥卡姆剃刀定律(Occam’s Razor)
- 含义:“如无必要,勿增实体”。反映到机器学习领域中,指的是在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。
- 简单的模型一方面指的是简单的hypothesis,即模型使用的特征比较少,例如多项式阶数比较少。另一方面指的是模型H包含的hypothesis数目有限,不会太多。实际上,hypothesis特征数目越少,H中hypothesis数目也就越少。
- 从哲学的角度:机器学习的目的是“找规律”;而对于简单的模型而言,其成长函数\(m_H(N)\)较小,故对一堆混乱的数据,能找到最优解的概率\(\frac{m_H(N)}{2^N}\)也很小。反过来说,如果简单的模型能找到这堆数据的最优解,则说明这堆数据肯定有规律。但是对于复杂模型则不然,复杂模型的表达能力很强,即便一堆数据没有规律,它也能找到最小的\(E_{in}\)。故即便复杂模型的\(E_{in}\)很小,也没法说明是这堆数据有规律,还是这个模型本身表达能力强的原因。
避免采样偏差(Sampling Bias),保证iid;
- 案例1:杜鲁门总统大选中,电话民意调查;(不合理抽样。此外银行贷款审批案例也有偏差的风险。)
- 案例2:Netflix推荐大赛中,林老师的将验证集准确率提高了13%,但最终比赛时却又少了7个百分点;(数据的分布是随时间序列而有一定变动的,测试集是按照最新的用户数据)
- 经验:训练和验证都要尽量匹配测试集场景。比如此处,可以增加近期数据的权重,验证集采用最新数据等等。
避免偷窥数据(Data snooping);
- 案例1:通过可视化,观察数据后人为定义模型(带入了人的主观想法);
- 案例2:将测试集数据混入训练集中一同训练;
- 案例3:一系列的paper针对同一个数据集D不断改进,相当于后面的paper偷窥了前面的模型;
- 解决方法:第一个方法是“看不见”数据。就是说当我们在选择模型的时候,尽量用我们的经验和知识来做判断选择,而不是通过数据来选择。先选模型,再看数据。第二个方法是平衡偷窥数据和验证的关系。

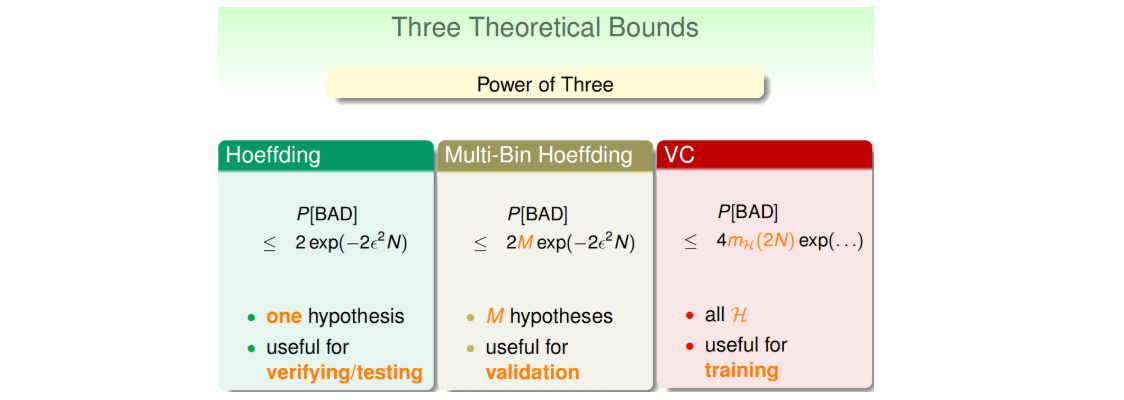
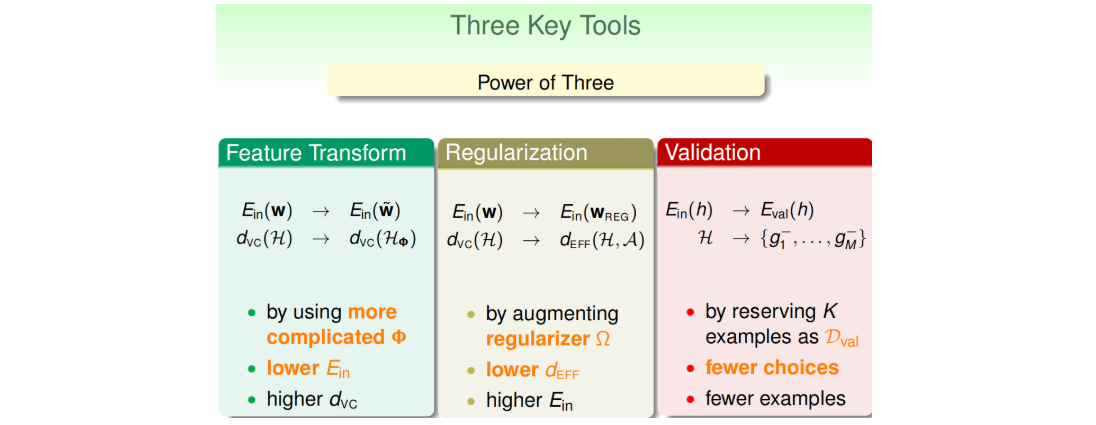
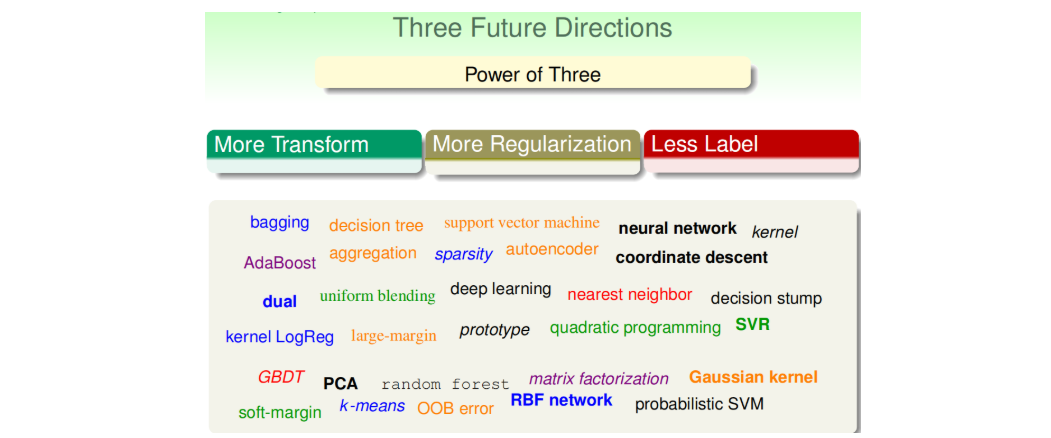
4.5 Summary: The Power Of Three