Word2Vec原理及代码
一、Word2Vec简介
Word2Vec 是 Google 于 2013 年开源推出的一款将词表征为实数值向量的高效工具,采用的模型有CBOW(Continuous Bag-Of-Words,连续的词袋模型)和Skip-gram两种。Word2Vec通过训练,可以把对文本内容的处理简化为K维向量空间中的向量运算,而向量空间上的相似度可以用来表示文本语义上的相似度。因此,Word2Vec输出的词向量可以被用来做很多NLP相关的工作,比如聚类、找同义词、词性分析等等。经过训练,部分单词向量的加法组合运算能达到类似于下面公式的效果:
vector('Paris') - vector('France') + vector('Italy') ≈ vector('Rome')
此外,下图也简洁明了的展示的Word2Vec的词向量特征。
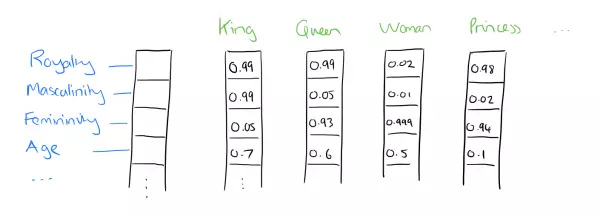
Word2Vec受欢迎的另一个原因是它的高效,具体思想可由Tomas Mikolov的两篇论文一探究竟。此文是我对Word2Vec学习的笔记。
二、分布式词表示(Distributed Representation)
自然语言处理的相关任务中,要想将自然语言处理交给机器学习中的算法处理,首先应该将语言数学化。在计算机运算中,向量可以说是人对机器输入的主要方式。而词向量,顾名思义,就是把一个词表示成一个向量,主要分为两种表示方法:One-Hot Representation 和 Distributed Representation。
我们知道,最简单的一种词表示方式是One-Hot表示,它的优点是很容易表示出不同的词,但是缺点也是巨大的:一、所有词向量正交,即无法刻画词与词之间的相似性。二、当有非常大的数据量时,向量的维度会因此扩大而造成维度灾难。如下所示,如果用One-Hot方式来表示自然界生物,自然界的动物种类数以百万记,因为数据量庞大,基本不可能用这种方式来表示动物类别,并且也无法表示诸如河虾、鲤鱼都生活在水里的这一相似性。
鲤鱼 [0,0,0,0,1,0,……,0,0,0,0,0,0,0]
河虾 [0,0,0,0,0,0,……,1,0,0,0,0,0,0]
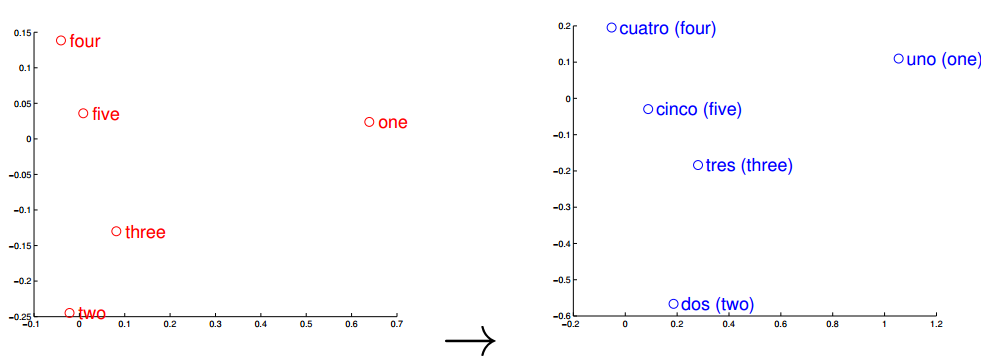
观察左右两图,可以发现:五个词在两个向量空间的相对位置差不多,说明了两种语言对应向量空间结构之间具有相似性,进一步说明词向量在刻画词与词相关性是合理的。
三、CBOW与skip-gram
语言模型形式化的描述就是给定一个T个词的字符串s,看他是自然语言的概率。举个例子:P(我,爱,学习,机器学习)= P(我)P(爱 | 我)P(学习 | 我,爱)P(机器学习 | 我,爱,学习)。这就是一种上下文相关的语言模型。但当碰到一个很长的语料,如果把一个词的出现要和前边所有出现过的单词联系起来,是非常复杂并且难以计算的。19世纪到20世纪初,俄罗斯数学家马尔科夫(Andrey Markov) 提出:假设任意一个词 wt 出现的概率只同他前面的词 wt-1 有关,问题就变得简单了。这种假设在数学上称为马尔科夫假设。
CBOW全称Continuous Bag-of-Words Model,Skip-Gram全称Continuous skip-gram Model。两者是Word2Vec里重要的两种模型,CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量,而输出就是这特定的一个词的词向量。Skip-Gram模型和CBOW的思路是反着来的,即输入是特定的一个词的词向量,而输出是特定词对应的上下文词向量。这两种模型都包含三层,输入层、投影层、输出层:
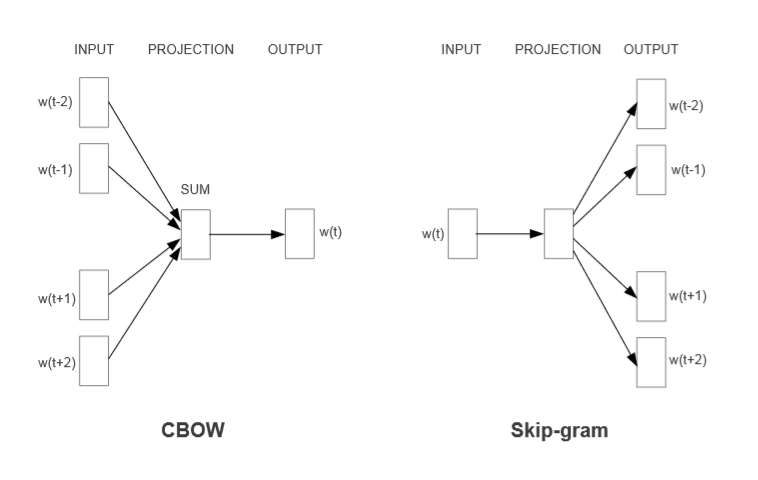
由上图可见,CBOW是在已知当前词 wt 的上下文 wt-2,wt-1,wt+1,wt+2 的前提下预测当前词wt;而Skip-gram则是已知当前词 wt 的前提下 ,去预测 wt-2,wt-1,wt+1,wt+2 。
四、Hierarchical Softmax框架与Negative Sampling框架
这两者并不是Word2Vec的精髓,只是Word2Vec的训练技巧。Hierarchical Softmax本质是把 N 分类问题变成 log(N) 次二分类; Negative Sampling 本质是预测总体类别的一个子集。
Hierarchical Softmax 和 Negative Sampling是Word2Vec设计的两种实现框架。Hierachical Softmax的基本思想是:它把训练语料中的词当成叶子节点,其在语料中出现的次数当做权值,通对于词典Dictionary中的任意词 w,Huffman 树中必存在一条从根节点到词 w 对应结点的路径,由此每个词对应一个Huffman编码。而 Negative Sampling 不再使用复杂的 Huffman树,而是采用随机负采样,可以减少训练时间和大幅度提高性能。
何为负采样算法呢?训练一个神经网络,样本只要有所改变(添加、修改、删除)就需要稍微调整所有的神经网络权重,这样才能确保训练结果的准确性。如果有一个巨大数据集,一个样本的改变都会改变神经网络的权重,代价是高昂的。而负采样的好处是,每一个训练样本仅仅改变一小部分的权重而不是所有的权重,解决了这个问题。比如,当我要进行对 ”ready“ 这个单词进行训练时,使用负采样,随机选择较少数目(小样本一般为5~20个,大样本为2~5个)的 ”负“ 样本进行权重更新,并且仍然为我们的 ”正“ 单词更新其对应的权重。词典 Dictionary 中的词在语料Corpus中出现的次数不同,那么对于高频词而言,被选为负样本的概率就应该比较大,而对于低频词,被选中的概率就应该小。
如果我们的输出层大约有 300 x 10,000 维度的权重矩阵,对 ”quick“ 一次进行权重更新,加上额外5个 负样本的权重更新,一共是6个输出神经元,和1800个权重值。这些值,仅仅只占输出层 3,000,000 神经元中的 0.06%。
五、代码实现
此代码已上传github,点击此处查看。网上有很多关于Word2Vec的实现,本文最初参考此代码以及一些现成代码,在后边的参考文章中列举。
import collections import math import os import random import zipfile import numpy as np import urllib import tensorflow as tf import matplotlib.pyplot as plt from sklearn.manifold import TSNE # Step 1 : 准备数据文档 url = 'http://mattmahoney.net/dc/' def download_check(filename, expected_bytes): """下载数据集,如果存在就确认跳过.""" if not os.path.exists(filename): print('正在下载所需数据包 …') filename, _ = urllib.request.urlretrieve(url + filename, filename) statinfo = os.stat(filename) if statinfo.st_size == expected_bytes: print('确认为目标文件 ', filename) else: print(statinfo.st_size) raise Exception( '文件大小不对应 ' + filename + '请前往 http://mattmahoney.net/dc/text8.zip 获取数据集') return filename filename = download_check('text8.zip', 31344016) # Step 2 : 解压文件 def read_data(filename): """读取zip的第一个文件并且分割单词为字符串数组""" with zipfile.ZipFile(filename) as f: data = tf.compat.as_str(f.read(f.namelist()[0])).split() return data words = read_data(filename) print('数据长度', len(words)) vocabulary_size = 50000 # Step 3 : 准备数据集 def build_dataset(words): """在字典第一个位置插入一项“UNK"代表不能识别的单词,也就是未出现在字典的单词统一用UNK表示""" # [['UNK', -1], ['i', 500], ['the', 498], ['man', 312], ...] count = [['UNK', -1]] # dictionary {'UNK':0, 'i':1, 'the': 2, 'man':3, ...} 收集所有单词词频 count.extend(collections.Counter(words).most_common(vocabulary_size - 1)) # python中K/V的一种数据结构"字典 dictionary = dict() for word, _ in count: dictionary[word] = len(dictionary) data = list() unk_count = 0 for word in words: if word in dictionary: index = dictionary[word] else: index = 0 # dictionary['UNK'] unk_count += 1 data.append(index) count[0][1] = unk_count reverse_dictionary = dict(zip(dictionary.values(), dictionary.keys())) return data, count, dictionary, reverse_dictionary data, count, dictionary, reverse_dictionary = build_dataset(words) del words print('词频最高的词', count[:5]) print('数据样例', data[:10], [reverse_dictionary[i] for i in data[:10]]) data_index = 0 # Step 4 : skip-gram def generate_batch(batch_size, num_skips, skip_window): global data_index #global关键字 使data_index 可在其他函数中修改其值 assert batch_size % num_skips == 0 #assert断言用于判断后者是否为true,如果返回值为假,处罚异常 assert num_skips <= 2 * skip_window batch = np.ndarray(shape=(batch_size), dtype=np.int32) #ndarray对象用于存放多维数组 labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32) span = 2 * skip_window + 1 # [ skip_window target skip_window] # 初始化最大长度为span的双端队列,超过最大长度后再添加数据,会从另一端删除容不下的数据 # buffer: 1, 21, 124, 438, 11 buffer = collections.deque(maxlen=span) #创建一个队列,模拟滑动窗口 for _ in range(span): buffer.append(data[data_index]) data_index = (data_index + 1) % len(data) for i in range(batch_size // num_skips): # // 是整数除 # target : 2 target = skip_window # target label at the center of the buffer # target_to_avoid : [2] targets_to_avoid = [ skip_window ] # 需要忽略的词在当前的span位置 # 更新源单词为当前5个单词的中间单词 source_word = buffer[skip_window] # 随机选择的5个span单词中除了源单词之外的4个单词中的两个 for j in range(num_skips): while target in targets_to_avoid: target = random.randint(0, span - 1) targets_to_avoid.append(target) # 已经经过的target放入targets_to_avoid #batch中添加源单词 batch[i * num_skips + j] = source_word #labels添加目标单词,单词来自随机选择的5个span单词中除了源单词之外的4个单词中的两个 labels[i * num_skips + j, 0] = buffer[target] # 往双端队列中添加下一个单词,双端队列会自动将容不下的数据从另一端删除 buffer.append(data[data_index]) data_index = (data_index + 1) % len(data) return batch, labels # Step 5 : 构建一个包含隐藏层的神经网络,隐藏层包含300节点,与我们要构造的WordEmbedding维度一致 batch, labels = generate_batch(batch_size=8, num_skips=2, skip_window=1) # 打印数据样例中的skip-gram样本 for i in range(8): print('(',batch[i], reverse_dictionary[batch[i]], ',', labels[i, 0], reverse_dictionary[labels[i, 0]],')') """ ( 3081 originated , 12 as ) ( 3081 originated , 5234 anarchism ) ( 12 as , 6 a ) ( 12 as , 3081 originated ) ( 6 a , 12 as ) ( 6 a , 195 term ) ( 195 term , 6 a ) ( 195 term , 2 of ) """ batch_size = 128 embedding_size = 128 # Demension of the embedding vector skip_window = 1 # How many words to consider left and right num_skips = 2 # How many times to reuse an input to generate a label valid_size = 16 # Random set of words to evaluate similarity on valid_window = 100 # Only pick dev samples in the head of the distribution valid_examples = np.random.choice(valid_window, valid_size, replace=False) num_sampled = 64 # Number of negative examples to sample graph = tf.Graph() with graph.as_default(): # 定义输入输出 train_inputs = tf.placeholder(tf.int32, shape=[batch_size]) train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1]) valid_dataset = tf.constant(valid_examples, dtype=tf.int32) # 当缺少GPU时,用CPU来进行训练和操作变量 with tf.device('/cpu:0'): # 初始化embedding矩阵,后边经过多次训练后我们得到的结果就放在此embedding矩阵; # tf.Variable是图变量,tf.radom_uniform产生一个在[-1,1]间均匀分布的size为[vocabulary_size, embedding_size]的矩阵 embeddings = tf.Variable( tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)) # 将输入序列转换成embedding表示, [batch_size, embedding_size] # tf.nn.embedding_lookup的作用就是找到要寻找的embedding data中的对应的行下的vector emded = tf.nn.embedding_lookup(embeddings, train_inputs) # 初始化权重,此处使用负例采样NCE loss损失函数 # tf.truncated_normal(shape, mean, stddev) :shape表示生成张量的维度,mean是均值,stddev是标准差。这个函数产生正太分布, # 均值和标准差自己设定。这是一个截断的产生正太分布的函数,就是说产生正太分布的值如果与均值的差值大于两倍的标准差,那就重新生成。 nce_weights = tf.Variable( tf.truncated_normal([vocabulary_size, embedding_size], stddev=1.0 / math.sqrt(embedding_size))) nce_biases = tf.Variable(tf.zeros([vocabulary_size])) # Compute the average NCE loss for the batch # tf.nce_loss automatically draws a new sample of the negative labels each # time we evalute the loss loss = tf.reduce_mean( tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, labels = train_labels, inputs = emded, num_sampled = num_sampled, num_classes = vocabulary_size )) # 使用1.0的速率来构造SGD优化器 optimizer = tf.train.GradientDescentOptimizer(1.0).minimize(loss) # 计算 minibatch 和 all embeddings的余弦相似度 # tf.reduce_sum() 按照行的维度求和 norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True)) normalized_embeddings = embeddings / norm valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset) # tf.matmul 矩阵相乘 similarity = tf.matmul(valid_embeddings, normalized_embeddings, transpose_b=True) # 添加变量初始化程序 init = tf.global_variables_initializer() # Step 6 : 开始训练 # 训练次数 num_steps = 100001 # tf.Session 用于运行TensorFlow操作的类 with tf.Session(graph=graph) as session: # 我们必须在使用之前初始化所有变量 init.run() print("Initialized") average_loss = 0 for step in range(num_steps): batch_inputs, batch_labels = generate_batch( batch_size, num_skips, skip_window) feed_dict = {train_inputs : batch_inputs, train_labels : batch_labels} # We perform one update step by evaluating the optimizer op( including it # in the list of returned values for session.run()) _, loss_val = session.run([optimizer, loss], feed_dict=feed_dict) average_loss += loss_val if step % 2000 == 0: if step > 0: average_loss /= 2000 #The average loss is an estimate of the loss over the last 2000 batches. print("Average loss at step", step, ": ", average_loss) average_loss = 0 # Note that this is expensive ( ~20% slowdown if computed every 500 steps) if step % 10000 == 0: sim = similarity.eval() for i in range(valid_size): valid_word = reverse_dictionary[valid_examples[i]] top_k = 8 # number of nearest neighbors nearest = (-sim[i, : ]).argsort()[1:top_k+1] log_str = "与 %s 最接近的词是:" % valid_word for k in range(top_k): close_word = reverse_dictionary[nearest[k]] log_str = "%s %s," % (log_str, close_word) print(log_str) final_embeddings = normalized_embeddings.eval() # Step 7 : 绘制结果 def plot_with_labels(low_dim_embs, labels, filename='TSNE_result.png'): assert low_dim_embs.shape[0] >= len(labels), "More labels than embeddings" plt.figure(figsize=(18, 18)) # in inches for i, label in enumerate(labels): x, y = low_dim_embs[i,:] plt.scatter(x, y) plt.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points', ha='right', va='bottom') plt.savefig(filename) # 使用T-SNE算法将128维降低到2维 tsne = TSNE(perplexity= 30, n_components = 2, init = 'pca', n_iter = 5000, random_state = 1) # 绘制点的个数 plot_only = 100 low_dim_embs = tsne.fit_transform(final_embeddings[: plot_only, :]) labels = [reverse_dictionary[i] for i in range(plot_only)] plot_with_labels(low_dim_embs, labels) plt.show()
六、训练结果
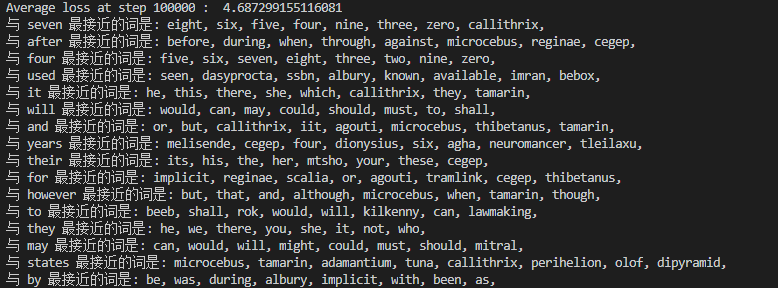
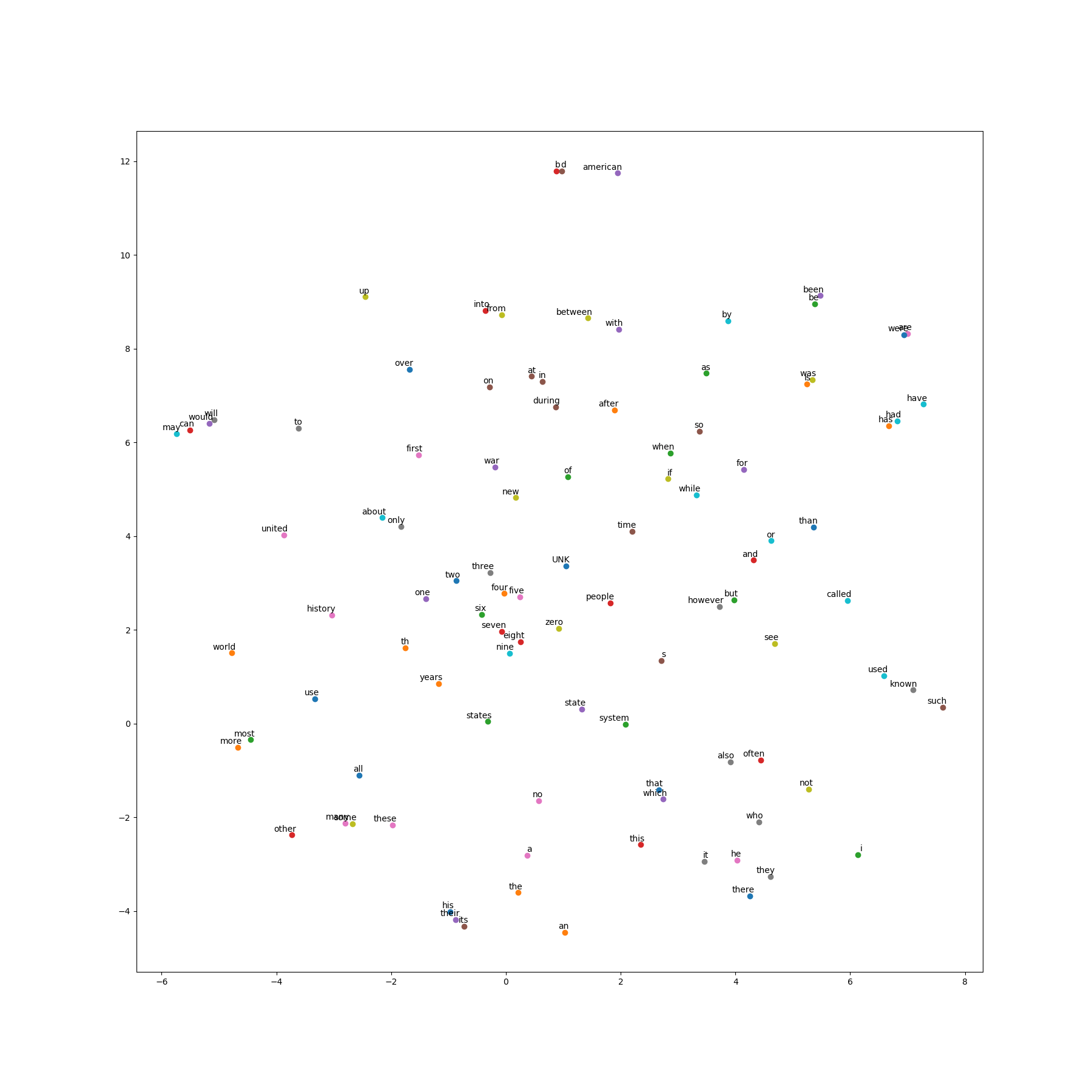
参考资料:
1、https://www.jianshu.com/p/471d9bfbd72f
2、https://www.jianshu.com/p/0bb00eed9c63
3、https://blog.csdn.net/itplus/article/details/37998797
4、https://blog.csdn.net/qq_28444159/article/details/77514563



 浙公网安备 33010602011771号
浙公网安备 33010602011771号