Codeforces 赛时没想出来的思维题集

Constructive Algorithm

60D Savior

给你正整数数组 \(a_n\)，对于 \(1\le i<j\le n\)，如果存在正整数 \(b\) 使以 \(a_i,a_j,b\) 为边的三角形为直角三角形，且 \(a_i,a_j,b\) 两两互质，则 \(i,j\) 是一类的。求有多少类。
\(n\le 10^6,a_i\le 10^7\)。

sol

数学构造题，锻炼思维推导能力。
考虑对于每一组满足三元组中较小的两个在 \(10^7\) 范围内的三元组将可以合并的数值合并。可以证明 \((x^2-y^2,2xy,x^2+y^2),\forall x,y\in\mathbf{N^*}\) 可以穷尽互质勾股数组。只需要有序地枚举 \(x,y\)，将三元组中在 \(a\) 中出现过的数两两合并，并在合适的时候 break 即可。注意，如果不是在 \(a\) 中出现的数合并了，就可能会导致不合法地归于同一类。
notes: long long
submission *2500

1641B Repetitions Decoding

给你一个长为 \(n(n^2\le 2\cdot 10^5)\)序列 \(a(a_i\le 10^9)\)，你可以在序列的任意两数之间/首尾，添加两个相同的数（任意），你需要使用不超过 \(2n^2\) 次操作使序列满足：

• 存在一种将 \(a\) 划分成若干非空段的方案，使得每一段长为偶数且前一半等于后一半。

你需要输出操作方案和划分方案。

sol

做出来了，但还是对我而言比较有意思的构造题。
我的构造方式是 \(las\) 从 1 开始，\(i\) 从 2 开始，每次找到第一个 \(a_i=a_{las}\) 的位置，并将 \(las+1\sim i-1\) 给复制（插入）到 \(i\) 的后面，那么就会有一个对称的 \(i-1\sim las+1\)，而前面那一段就已经满足条件了。重复这样的操作，事实证明最后一定就不会有剩的了。观察到待处理序列的长度每次至少-1，这应该可以做“事实证明”的佐证，同时说明操作数\(\le n^2\)。那么无解当且仅当一个时刻找不到了一个 \(a_i=a_{las}\)，发现每次操作会将一些数的出现次数减去偶数，所以上面说的等价于最初存在一个 \(a_i\) 出现奇数次。做法跟题解可能不太一样吧，没看题解。

1736D Equal Binary Subsequences

sol

(1,2), (3,4), ..., (2n-1,2n) 地分组。那么每一组要么相同要么不同。考虑每个组一个分给一个子序列，另一个分给另一个子序列。对于相同的情况，随便给，对于不同的情况，我们把这些不同的情况的组先提出来，然后让每个组都分得一个 010101...01/101010...10 这种 01 交替的串，由于 1（0） 的个数显然得是偶数（不然无解），所以交替串的长度一定是偶数，如果两者相等，啥都不干，否则循环移位后一定相等。*2200

1730D Prefixes and Suffixes

sol

寻找普遍规律，那就普遍地设，设成 \(s_1s_2s_3s_4s_5\) 和 \(t_1t_2t_3t_4t_5\)，然后模拟一次操作：\(t_3t_4t_5s_4s_5\) 和 \(t_1t_2s_1s_2s_3\)。不难发现 \(s_i\) 和 \(t_{n+1-i}\) 始终是关于中轴线对称的，而且感性理解可知这也是状态可达的充分条件。因此只需要判断所给状态的每一对 \(s_i\) 和 \(t_{n+1-i}\)，我们把它记为一个 char 的 pair \((c_1,c_2)(c_1\le c_2)\)，那么可相等显然等价于每个等价类的大小为偶数，或恰好一个为奇数且这个等价类的 first 和 second 相等（\(n\) 为奇数的情况）。*2200

Combinatorics

1546D AquaMoon and Chess

你有一个长为 \(n\) 的棋盘,这个棋盘上有一些棋子，你可以进行如下操作:

• 如果第 \(i + 2\) 个位置是空的，且第 \(i+1\) 个位置非空，则可以将第 \(i\) 个位置的棋子挪到第 \(i + 2\) 个位置 \((i + 2 \leq n)\)。
• 如果第 \(i - 2\) 个位置是空的，且第 \(i - 1\) 个位置非空，则可以将第 \(i\) 个位置的棋子挪到第 \(i - 2\) 个位置 \((i - 2 \geq 1)\)。
  现在将给出一个棋盘的初始状态，求可以通过上述操作可以到达的状态数，你可以进行任意次操作，答案对 \(998244353\) 取模。

sol

一句话题解：11 是自由元，1 是被动移动元，任何一种方案可以看做是 11 自己移动过去然后 1 被挤到挨着的地方，因此方案由 11 和 0 的组合顺序决定，答案为 \(C_{a+b}^a\)，其中 \(a,b\) 表示 11 和 0 的个数。

---

真的是一句话可以说清楚的吗？显然不是，这道题思维难度对于我来说是很大的，也没做出来。从这题要学到以下几点

1. 从一个方便分析的视角来看组合问题的结构
2. 考虑主动元就是考虑整个问题，被动元的影响是忽略的（原因是已经包含在主动元的影响内了）
3. 2 种数，每种 \(a,b\) 个，形成的组合数量为 \(C_{a+b}^a\) *1900

1172B Nauuo and Circle

算是自己想出来了吧，但还是相当经典的题目。

sol

从树形 dp 角度考虑，设 \(f(u)\) 表示 \(u\) 的子树内节点的排列方案数，显然不同儿子的子树是互相独立不能交叉的（可以这样理解），因此其排列方案数为 \(f(u)=\prod_{v\in son(u)}f(v)\cdot (|son(u)|+1)\)，但是这个式子对于根节点是错的，因为这时外面已经没有点了，所以根（钦定是1）插在0和deg+1处是等价的。根据题意最上面的点不同算不同方案，所以答案就是 \(f(1)\times n\)。这个化简后就是 \(\prod_{i=1}^n deg_i!\times n\)。

1705D Mark and Lightbulbs

两个长为 \(n(n\le 2\times 10^5)\) 的 01 串 \(s,t\)，通过以下操作，将 \(s\) 变成 \(t\)，最少多少步？

• 选择一个 \(2\le i\le n-1\)，使得 \(s_{i-1}\ne s_{i+1}\)，并反转 \(s_i\)

sol

观察循环不变式（其实这个跟 Aquamoon and Chess 好像挺像而且更加简单）。Chunks of \(1\)s remain where they are（相对位置）。如果 number of chunks of \(1\)s of \(s\) and \(t\) 不等，抑或是 \(s_1\ne t_1\) or \(s_n\ne t_n\)，那么显然 -1。否则逐个计算把 \(s\) 的第 \(i\) 个 chunk of \(1\) 变到 \(t\) 的第 \(i\) 个 chunk of \(1\) 要几步，即可，不赘述。
submission

1696E Placing Jinas

初始时在 \((0,0)\) 处有一个玩偶，每次可以选择一个 \((i,j)\) 处的玩偶，删除它，并在 \((i,j+1),(i+1,j)\) 两处放置玩偶，一个位置允许有多个玩偶。\(\forall i\in [0,n],(i,0),(i,1),...,(i,a_i-1)\) 是白点，所有其他地方是黑点。问将所有玩偶都移到黑点的操作次数 \(\bmod (10^9+7)\)。

sol

移动时发现 \((i,j)\) 上的玩偶会全部累加到 \((i,j+1),(i+1,j)\)，故考虑递推。设 \(f(i,j)\) 表示对 \((i,j)\) 上的玩偶操作次数，转移关系 \(f(i,j)=f(i-1,j)+f(i,j-1)\)。这个式子很简洁，按照套路可以看成 \((0,0)\to (i,j)\) 的行走方案数（每次只能往右和往下），即 \(i+j\choose i\)。
答案即为 \(\sum_{i=0}^n\sum_{j=0}^{a_i-1}{i+j\choose i}=\sum_{i=0}^n{i+a_i\choose i+1}\)

1717D Madoka and The Corruption Scheme

你来任意给出一个 \(2^n\) 的排列，依次放到一个 \(n+1\) 层的满二叉树的叶子结点的编号上，第 \(1\sim n\) 层的每个点的编号由你决定，可以是左儿子编号或右儿子编号。裁判可以更改至多 \(k\) 个点的编号的决定方式（左变右、右变左）（注意祖先都会跟着变）。你希望通过调整排列的顺序和初始决定方式，来使得最后根节点上的编号在最坏情况下最小。求最坏情况下的值最小是多少。\(n\le 10^5,k\le 10^9\)

sol

更改恰好 \(i\) 个点，可以获得的不同 outcome 会有 \(n\choose i\) 种，因为每一层都至多更改一个点。那么答案就是 \(\sum_{i=0}^{\min(k,n)}{n\choose i}\)

1830C Hyperregular Bracket Strings

求有多少个长度为 \(n\) 的合法括号序列 \(a\)，使得 \(a[l_1:r_1],a[l_2:r_2],\dots,a[l_K:r_K]\) 都是合法括号序列。\(n,K\le 3\times 10^5\)

sol

将 \(1\sim n\) 按照被哪些区间覆盖分成等价类，这可以利用随机哈希权值区间 xor 得到。
不难通过分类讨论发现每个等价类是独立的，并且一个大小为 \(len\) 的等价类贡献 \(\times {{len\choose len/2}\over {len/2+1}}\)（卡特兰数）。

1264D Beautiful Bracket Sequence

一个合法括号序列的深度定义为其括号树的高度（两个点的树高度为2），一个括号序列的权值定义为其所有合法括号子序列的深度的最大值。有一个长度为 \(n(n\le 10^6)\) 的包含 ? 的括号序列，求所有补全方案的权值之和。

sol

首先考察一个确定括号序列的权值怎么求。任何一个深度为 \(d\) 的括号序列 \(t\) 都可以简化成形如 (((()))) 的由 \(d\) 个 ( 和 \(d\) 个 ) 依次组成的序列。因此可以通过枚举中间的间隙 \(1\le i\le n\) 得到答案：\(\max_{i}\min(\#{\tt{(}}[1,i],\#{\tt{)}}[i+1,n])\)。
将后面的部分它看成关于 \(i\) 的函数，则单峰，并且由于两边的函数都连续，所以一定有一个位置取到 \(\#{\tt{(}}[1,i]=\#{\tt{)}}[i+1,n]\)，这就是答案。设 \(S_i=\#{\tt{(}}[1,i]\)，则 \(\#{\tt{)}}[i+1,n]=(n-S_n)-(i-S_i)\)，列出 \(S_i=(n-S_n)-(i-S_i)\)，惊奇地发现 \(i=n-S_n\)，于是答案就是所有填法方案的 \(S_{n-S_n}\) 之和。
枚举 \(S_n\)，记 \(a\) 为 \(\le n-S_n\) 的 \(\# ?\)，\(b\) 为 \(>n-S_n\) 的 \(\# ?\)，\(c\) 为 \(\le n-S_n\) 已有的 \((\)，\(d\) 为 \(> n-S_n\) 已有的 \((\)，答案就是 \(\sum_{n=0}^{S_n}(c+i){a\choose i}{b\choose S_n-i-c-d}\)，化简得 \(c{a+b\choose S_n-c-d}+a{a-1+b\choose S_n-1-c-d}\)。

1646E Power Board

\(n\times m\) 的二维数组 \(a_{i,j}=i^j\)，求其中有多少个不同的数。\(n,m\le 10^6\)。

sol

题意简单，但不是很简单。

法1【预处理】 非常容易想到，如果一个数出现在两个地方，那么 \(i_2\) 一定是 \(i_1\) 的幂次(\(i_2>i_1\))。很重要的是，对每一个这种集合单独开来处理，那么对于现在的一排 \(x,x^2,...\)，它们构成：

x   x^2  x^3  ... x^m
x^2 x^4  x^6  ... x^2m
...
x^r x^2r x^3r ... x^rm

省去累赘的底数，每一排就是 i 2i ... mi。而 \(r\le \log n\le 20\)，我们要的就是这个 \(20\times m\) 的矩阵的一个前缀行构成的矩阵，容易想到对它预处理（暴力都行）。
法2【容斥】 （可以处理 \(m\le 10^{18}\)）前面一部分思路跟上面一样，问题化成对 \(1\le k\le r,1\le j\le m\)，求 \(ij\) 互异的个数。你容斥一个 \(mask<2^r\) 表示要表达的数 \(x\) 必须同时是 \(mask\) 所选的 \(k\) 的倍数（记分别选的 \(a_0,a_1,...(a_i<a_{i+1})\)），即是 \(lcm\) 的倍数。设 \(x=a_0b_0=a_1b_1=...=lcm\cdot y\)，则显然最大的 \(b\) 是属于 \(a_0\) 的，那么要想 \(y\) 最大 \(x\) 必须最大，于是 \(lcm\cdot y\le a_0\cdot m\)，\(y\le m/(\frac {lcm}{a_0})\)，这就是 \(mask\) 的答案。

Interactive

1172D' Nauuo and Binary Tree

有一棵 \(n(n\le 3000)\) 个点的二叉树，你需要通过最多 \(30000\) 次对树上两点距离的询问，得到这棵树。

sol

不难想到第一步询问根到每个点的距离得到每个点所在的层。现在的问题是如何在已知上面所有层的情况下确定这一层的各点父亲。
\(30000\approx n\log n\)，有树链剖分提示。对于已经确定的这前若干层树链剖分，询问一个重链末端到一个待定点的距离，如果是 \(1\) 则待定点的父亲即为该重链末端，否则根据 \(dep_u+dep_v-2dep_{\text{lca}(u,v)}=\text{dist}(u,v)\) 可得到 \(lca\) 是哪个点，并知道应该朝着不是重边的方向去走，递归地再去询问这个走到的点所在的重链末端到原来待定点的距离，等等等等，最终可用 \(O(\log n)\) 确定一个待定点。
树链剖分的常数较小，实际上 \(30000\) 次询问绰绰有余。

1584D Guess the Permutation

【交互题】给定数组 \(a=\{1,2,3,...,n\}\)，现在评测机选定 \(i,j,k\in [1,n](i<j-1,j<k)\)，并翻转 \(a_{[i,j-1]},a_{[j,k]}\)。你只知道 \(n(4\le n\le 10^9)\)，需要在不超过 40 次询问后给出 \(i,j,k\)，每次询问“? l r”可以得到子段 \(a_{[l,r]}\) 中的逆序对数。

sol

一句话题解：考虑首先二分求出 \(i\)，并由 \(ask(i,n)-ask(i+1,n)+1\) 求得 \([i,j-1]\) 的长度，同理 \(ask(j,n)-ask(j+1,n)+1\) 求得 \([j,k]\) 的长度。

---

具体地，我们可以利用二分找出最后一个 \(ask(1,p)=0\) 的 \(p\)，那么显然 \(i=p\)。接下来考虑 \(ask(i,n)-ask(i+1,n)\) 会得到什么，那么就是减少了 \(a_i\) 跟后面构成的逆序对数，那因为 \(a_i\) 只会跟 \(a_{i+1}...a_{j-1}\) 构成逆序对，所以 \((j-1)-(i+1)+1=ask(i,n)-ask(i+1,n)\)，换句话说就是 \(j-1=i+ask(i,n)-ask(i+1,n)\)。那么同理地，\(k=j+ask(j,n)-ask(j+1,n)\)。
notes: long long
submission *2000

1634D Finding Zero

【交互题】猜测含有恰好一个 0 的数组 \(a\) 中 0 的两个可能位置：! i j 表示回答“\(a_i=0\) 或 \(a_j=0\)”；通过不超过 \(2n-2\) 次询问：? i j k 表示询问 \(\max(a_i,a_j,a_k)-\min(a_i,a_j,a_k)\)。

sol

题目可转化为确定 \(n-2\) 个必不为 0 的位置。
先考虑 \(n=4\) 情况下如何找到。不妨设四个数分别为 \(a<b<c<d\)，令 \(\overline a\) 表示 \(Q(b,c,d)=\max(b,c,d)-\min(b,c,d)\)，\(\overline b=Q(a,c,d),\overline c=Q(a,b,d),\overline d=Q(a,b,c)\)，则：

\[\overline a=d-b\\ \overline b=d-a\\ \overline c=d-a\\ \overline d=c-a\\ \therefore \overline b=\overline c>\overline a,\overline d \]

而 \(b,c>0\) 因此可以确定两个必不为 0 的位置。

考虑 \(n>4\) 的情况，可以每次将排除后待定的两个元素跟后面的两个元素又组成一个四元组来确定。最后会剩下 2 或 3 个数，前者直接输出，后者把前面已经确定不是 0 的元素不妨再丢进来组一下。
询问次数：\(n\) 是奇数时 \(4(\frac{n+1}{2}-1)=2n-2\)，\(n\) 是偶数时 \(4(\frac{n}{2}-1)=2n-4\)。

submission

Observation

ABC200D Happy birthday!2

对数列 \(a_n(2\le n\le 200,1\le a_i\le 10^9)\) 找到两个不同的子序列使得和模 \(200\) 相同。输出方案或判断无解。

sol

评分极低的一道题，但脑筋急转弯不小。基于鸽巢原理暴力 dfs 并在超过 201 时 exit。

1546C AquaMoon and Strange Sort

给你整数数组 \(a_1,a_2,...,a_n(n\le 10^5,0<a_i\le 10^5)\)，你可以交换任意相邻元素任意次，每执行一次交换操作被执行元素分别变成自己的相反数，例如 -1 1 2，若交换 \(a_2,a_3\) 则得到 -1 -2 -1，若交换 \(a_1,a_2\) 则不变。求能否使得 \(a\) 单调不降且各元素 \(>0\)。

sol

\(a_i\) 从 \(i\) 移动到 \(j\)，执行的交换操作奇偶性一定和 \(|i-j|\) 相同，那么由于 \(a_i\) 的正负不变，一定被交换了偶数次，于是 \(i\) 和 \(j\) 的奇偶性相同；设 \(f_{i,0},g_{i,0},f_{i,1},g_{i,1}\) 分别表示数值 \(i\) 在原数组奇数位、偶数位出现的次数和在递增排序后的新数组奇数、偶数位出现的次数，则有解等价于 \(f_{i,0}=f_{i,1}\) 且 \(g_{i,0}=g_{i,1}\)。

个人认为维难度不小，同时数据很强。submission *1500

1838D Bracket Walk

给定一个括号序列 \(s(n=|s|\le 2\times 10^5)\)，\(q(q\le 2\times 10^5)\) 次单点翻转一个位置的括号，每次修改后输出 \(s\) 是否是“可走”的。
一个括号串是可走的当且仅当可以从 \(1\) 出发，每次移到左右相邻格子之一，到达 \(n\) 时依次经过的字符恰好构成合法括号序列。

sol

感觉对我来说思维难度好大啊！

对于一个串，怎样判定它是否合法呢？首先你会发现，(( 和 )) 是我们的工具，但是如果第一个 (( 出现得太晚（最后一个 )) 出现得太早）也不行。那什么叫出现得太晚？妨碍我们的又是什么？是 )) 啊！设想如果前面全都没有 )，这里出现了一个 ))，不正是第一个非法位置吗？因此只需要判断第一个 )) 和第一个 (( 的位置关系、最后一个 )) 和最后一个 (( 的位置关系即可，有了这两个条件，中间的抵消就不成问题了！而细节上，还要特判 \(s_1\) 为 )/\(s_{n}\) 为 (/\(n\) 为奇数的无解情况。

1468D Max Median

序列 \(a_n\) 的长 \(\ge k\) 的区间的中位数最大值？

sol

套路题 “最大”想到二分答案，但是发现中位数 \(\ge x\) 很难量化，于是容易弃此路。
事实上，要解决「固定 \(x\)，求是否有长 \(\ge k\) 的区间中位数 \(\ge x\)」之类问题（或可拓展至关于中位数大小限制的许多问题），有一个套路是构造序列 b[i]=a[i]>=x?1:-1。
这样在本题中，就可以对 \(b\) 求前缀和并利用树状数组 check 了，不赘述。

*2100 submission //beware：初始的0的空前缀要加到及什么时候加到BIT。beware2:k=1的情况会让一些写法FST。data:1 1 1

CF1750E Bracket Cost

不难发现一个子串的答案是把匹配括号删去之后剩下的左括号和右括号数量的较大值。
事实证明，这样想是不好统计的，因为“删”这个动作太繁琐了。我们考虑把上面的表述量化：\(\max(L,R)-M\)，\(L,R,M\) 分别表示左括号数量、右括号数量、匹配括号数量。因此问题变为统计 \(\sum\max(L,R)\) 和 \(\sum M\)，后者容易通过栈模拟、从每组匹配括号贡献的角度计算。
前者的变形非常巧妙 \(\max(L,R)=\frac{L+R-|L-R|}2\)，其中 \(\sum (L+R)\) 易得，而 \(\sum |L-R|\) 可以看作把左右括号 ±1 赋值后的区间和之和，通过将 \(n+1\) 个前缀和排序统计。

[信友队图灵杯2022]回文多项式

多项式 \(A(x)=a_0x^0+a_1x^1+...+a_kx^k\) 是回文多项式当且仅当 \(\forall i,a_i=a_{k-i}\)。
给定 \(n\) 个多项式 \(A_i(x)\)（第 \(i\) 个多项式有 \(k_i\) 项，已知 \(a_{i,0\sim k_i}\)）。\(q\) 次询问 \([l_i,r_i]\) 内的多项式的乘积是否回文。
\(n,q\le 10^5,\sum k_i\le 5*10^5\)

sol

不该想不出。最关键在于转化“回文多项式”为 \(f(x)=x^kf(\frac1x)\)。那么随一个 \(x\) 带进去，每次查询区间乘积即可，对大质数取模。应该会 WA，所以用两个 \(x\)，这样可以证明错误率是 \(<10^{-5}\) 的。

1654F Minimal String Xoration

给定 \(s(|s|=2^n,n\le 18)\)，你来选一个 \(j\in [0,2^n-1]\)，使得 \(t_i=s_{i\oplus j}(i\in [0,2^n-1])\) 的串 \(t\) 字典序最小。输出字典序最小的 \(t\)。

sol

这个题的SA提示十分隐蔽，你得推出一个性质才能想到：
记 \(f(s,j)\) 表示 \(s\) 按照题意变换得到的 \(t\)，则：

\[f(s,x)[2^k,2^{k+1}-1]\\ =s[2^k\operatorname{xor}x]...s[(2^{k+1}-1)\operatorname{xor}x]\\ =s[2^k\operatorname{xor}0\operatorname{xor}x]s[2^k\operatorname{xor}1\operatorname{xor}x]...s[2^k\operatorname{xor}(2^k-1)\operatorname{xor}x]\\ =f(s,x\operatorname{xor}2^k)[0,2^k-1] \]

（神不神奇）
这就提示我们进行倍增，类似SA，我们按照 \(f(s,x)\) 的前 \(1,2,4,...,2^n\) 排序的 \(x\) 构成的数组分别记为 \(a_0,a_1,...,a_n\)，那么就可以由 \(a_{k-1}\) 推得按 \(f(s,x)[2^{k-1},2^k-1]\) 排序的 \(x\) 构成的数组，按照“前者的 rank 靠前的优先，相等的再看后者的 rank 靠前的优先，还相等就定成一样的 rank”，处理出 \(a_k\)，则 \(a_n\) 中的第一名就是满足条件的一个 \(j\)。

GYM103098D

【交互题】地上竖着 \(n(\le 500)\) 个轻质弹簧，有原长 \(h_i\) 和劲度系数 \(k_i(>0)\)，放上重力为 \(w(1\le w\le 10^5)\) 的物体后 \(H=h-\frac wk\)（弹簧长度可以为负）。
你可以做 \(\le 20000\) 个询问 ? i j w 表示问 \(i,j\) 弹簧放上 \(w\) 谁更低，返回 FIRST/SECOND/EQUAL。做完所有后输出一行一个 !。
给你若干（\(\le 1000\)）个询问 QUSETION w 表示问 \(1\sim n\) 中放上 \(w\) 谁最低，输出 ! i。FINISH 表示所有询问结束。

注：原题中每个询问前可以加上 \(20\) 次询问，这里不予考虑，因为去掉依然可做。

sol

交互平面几何+单调性思维题。
策略是一开始将所有弹簧按纵截距（\(x=1\)）小到大排序，依次加入并维护半平面交，其与当前半平面交必然至多只有 1 个交点，二分到它并更新。

Greedy and Sortings

1804D Accommodation

给定长度为 \(m(4\mid m,1\le m\le 5\times 10^5)\) 的 \(01\) 串 \(s\)，你需要把它划分为 \(\frac m4\) 个长为 \(2\) 的子串 + \(\frac m2\) 个长为 \(1\) 的子串，计算这 \(\frac 34 m\) 个串中有多少个包含至少一个 \(1\)，输出这个值的最大值和最小值。

sol

突破口是守恒关系：\(c1+c01+c10+2\cdot c11=k\)(\(k\) 为 \(s\) 中 1 的个数);\(c01+c10+c11=\frac m4\)
maximize \(c1+c01+c10+c11\Rightarrow\) minimize \(c11\Rightarrow\) maximize \(c01+c10\)
minimize \(c1+c01+c10+c11\Rightarrow\) maximize \(c11\)
于是贪心地选长为2的串即可。

1684E MEX vs DIFF

sol

1608C Game Master

有元组序列 \(\{(a_i,b_i)\}(n\le 10^5,a_i,b_i\le 10^9)\)，现进行 \(n-1\) 轮淘汰赛（输方直接退出比赛），定义 \((a_i,b_i)\) 胜过 \((a_j,b_j)\) 当且仅当 \(a_i>a_j\) 或 \(b_i>b_j\)。问每个元组有无可能成为总冠军。\(a_i\) 互异，\(b_i\) 互异。

sol

容易想到以 \(a_i\) 为关键字排序。从 \(n\to 1\) 枚举 \(i\)，\((a_i,b_i)\) 能成为总冠军当且仅当 \(\max_{j=1}^ib_j>\min_{j=i+1}^nb_j\)，若上述不等式不成立则 break（并且 \(1\sim i\) 都不可能是总冠军）。
这是因为：

• 首先，\(1\sim i-1\) 都是可以输给 \(i\) 的，而一旦上述不等式成立，就存在策略：先让 \(\min_{j=i+1}^n\) 所在的 \(j\) 把 \(\complement_{[i+1,n]}\{j\}\) 给全部征服（因为已经确定它是可能成为总冠军的），再让 \(\max_{j=1}^ib_j\) 存在的 \(j'\) 赢过 \(j\)，这样一来 \(>i\) 的元组都输了，即证。

submission

1612G Max Sum Array

sol

1039D You Are Given a Tree

给出树，对所有 \(1\le k\le n\) 输出点数为 \(k\) 的点不相交路径条数最大可能值。

sol

贪心 + 根号分治。
如何 \(O(n)\) 求给定 \(k\) 时的答案。dfs，每个点如果子树中能有两条满足 \(a+b+1\ge k\) 就贪心地用它并 ans++，然后 \(mx_u=0\)，否则 \(mx_u=\max mx_{v=uson}+1\)。
对 \(i<\sqrt B\)，用上面暴力算，\(O(n\sqrt B)\)。
观察到答案随 \(k\) 增大递减，所以对 \(i\ge sqrt B\)，答案 \(\le n/\sqrt B\)，可枚举答案（\(las\)），然后二分找到最大使得 \(ans=las\) 的 \(i\)，把当前位置~\(i\) 都变 \(las\)，复杂度 \(O(\frac n{\sqrt B}\cdot \log n)\)，取 \(B=n\log n\) 时最优复杂度 \(O(n\sqrt{n\log n})\)。

DP

1806D DSU Master

有 \(n\) 个不路径压缩并查集，最初第 \(i\) 个并查集是一个点 \(i\)。第 \(i\) 个点和第 \(i+1\) 个点之间有一条边，边权是 \(a_i\)。对每个 \(k=1\sim n-1\)，计数所有排列 \(\{p_k\}\) 的价值之和，价值的定义为依次考虑 \(1\sim i\)，然后把第 \(p_i\) 和 \(p_{i}+1\) 所在的并查集合并，\(a_{p_i}=0\) 代表将后者合并到前者，反之代表将前者合并到后者，价值即为最终点 \(1\) 的入度。\(n\le 5\times 10^5\)

sol

由于问的就是前 \(i\) 个，就只考虑前 \(i\) 条边；问的是“期望”，先求方案数。这时，我们考虑加入第 \(i\) 条边的影响。发现 \(a_{i}\) 是多少会影响，因此分讨，\(a_{i}=0\) 时，这条边 \(i\) 种插法都满足，所以 \(f_i=f_{i-1}\times i\)，\(a_i=1\) 时，不能最后做，其他都能插，所以是 \(f_i=f_{i-1}\times (i-1)\)。\(f\) 代表的是前 \(i\) 条边能够使 \(1\) 还是根的方案数，我们再设一个 \(g_i\) 表示前 \(i\) 条边的答案。\(a_i=0\) 时，首先 \(i\) 种插法，所以 \(g_i\gets g_{i-1}\times i\)，然后只有最后插才会增加点 1 的入度，所以 \(g_i\gets f_{i-1}\)；\(a_i=1\) 时，首先 \(i\) 种插法，然后不管插哪里都没贡献，所以直接 \(g_i=g_{i-1}\times i\)。

1816F XOR Counting

给定 \(n,m\)，求 \(\sum_{x=0}^n [\exists \{a_m\}\text{ s.t. }\sum{a_i}=n,\bigoplus{a_i}=x]x\)。\(0\le n\le 10^{18},1\le m\le 10^5\)

sol

第一个观察是 \(\bigoplus a_i\) 和 \(\sum a_i\) 奇偶性相同，因此当 \(m\ge 3\) 时，对于任意和 \(n\) 奇偶性相同的 \(x\le n\) 必然可以把 \(n\) 拆成 \(x\) 和两个 \((n-x)/2\)，答案是平凡的。
\(m=1\) 更平凡。现在重点需要解决的是 \(m=2\)，方法就是递推，但是据题解来看，还挺巧妙。
设 \(f(n),g(n)\) 表示和为 \(n\) 的两数的值不同 xor 的总和、个数。
对于 \(a\oplus b\)：若 \(n\) 为偶数，则有两种情况，第一种，\(a,b\) 均为奇数，令 \(a'=(a-1)/2,b'=(b-1)/2\)，则 \(a\oplus b=2(a'\oplus b'),a'+b'=n/2-1\)，第二种，\(a,b\) 均为偶数，令 \(a'=a/2,b'=b/2\)，则 \(a\oplus b=2(a'\oplus b'),a'+b'=n/2\)，因此 \(g(n)=g(n/2)+g(n/2-1)\)，\(f(n)=2f(n/2)+2f(n/2-1)\)；若 \(n\) 为奇数，则有一种情况，不妨设 \(a\) 奇 \(b\) 偶，令 \(a'=(a-1)/2,b'=b/2\)，则 \(a\oplus b=2(a'\oplus b')+1,a'+b'=(n-1)/2\)，因此 \(g(n)=g((n-1)/2)\)，\(f(n)=2f((n-1)/2)+g(n)\)。

submission

1614D2 Divan and Kostomuksha

重排数组 \(a(n\le 10^6,a_i\le 2\cdot 10^7)\)，使 \(\sum_{i=1}^n\gcd(a_1,a_2,...,a_i)\) 最大化，输出最大值。

sol

*2300

1695D Tree Queries

在 \(n\) 个点的树中选择 \(k\) 个点 \(v_{1..k}\)，使得对于任意 \(x\)，不存在 \(y\ne x\) 使 \(\forall i=1..k,dist(y,v_i)=dist(x,v_i)\)。\(n\le 2\times 10^5\)

sol

直接做不太好做，所以考虑能否树形 dp。子结构：对于根，如果有两个子树都不存在被选节点，则一定不能完全确定。因此至多一个儿子为空。并且所有儿子自己都要满足条件。（如果所有儿子都满足条件时不存在任何一棵空，就不能空；否则如果有多棵为空，则只留一个空，其他的各随便放一个）根的选择：任意度数 \(\ge 3\) 的节点（故须特判整棵树是链的情况），否则可能忽略父链为空。

1625E1 Cats on the Upgrade

给你一个含左右括号的括号序列 \(s\)（不保证合法），每次询问保证合法的括号子段 \(s[l...r]\)，问其中有多少个二元组 \((i,j)(l\le i<j\le r)\) 满足 \(s[i...j]\) 是合法括号序列。\(n,q\le 3\cdot 10^5\)。

sol

一句话题解：构造括号树+递推。

---

构造括号树（将每对括号看成一个节点，它所包含的括号是它的子孙，同级括号为兄弟），设 \(f[i]\)（s[i]==')'）表示括号树中 \(i\) 所在节点的兄弟们和自己如果按从左到右排列它自己排老几。由于不同层之间是独立选择区间的，所以你考虑每个节点以他为末就有 \(f[i]\) 种方案（前提是所有兄弟都在询问区间内），从而答案为 \(\sum_{i=l}^rf[i]\)；但前提不一定满足，由于 \(s[l-1]\) 一定跟 \(s[l]\) 是同级的，所以多算了 \(f[l-1]\cdot(f[r]-f[l-1])\)，减掉即可。\(f[i]\) 的递推方式为：s[i]=='(' 时 \(f[i]=0\)，否则 \(f[i]=f[stk[tp]-1]+1\)（\(stk[tp]\) 跟 \(i\) 匹配了）。

1648D Serious Business

一个 \(3*n\) 的矩阵 \(a\)，一三行可行、第二行全是障碍物。有 \(q\) 个可选操作：耗费 \(w_i\) 将 \(a_{2,[l_i,r_i]}\) 炸掉。从 \((1,1)\) 出发去往 \((3,n)\)，经过 \((i,j)\) 获得 \(a_{i,j}\) 价值，求总价值减总代价的最大值。\(n,q\le 5*10^5\)

sol

如果从第二行的位置入手的话很难列状态，应该从操作入手看能更新哪些 \(f[i]\)。具体地，设 \(f[i]\) 表示 \((1,1)\) 去 \((2,i)\) 的最小代价（这个很好想到），对于一个区间 \([l,r]\)，有：

\[f[i]\gets f[l-1]+pre_{2,i}-pre_{2,l-1}-w,\forall i\in [l,r]\\ f[i]\gets \min_{j\in[l,i]}(pre_{1,j}+pre_{2,i}-pre_{2,j-1}-w),\forall i\in[l,r] \]

两个式子中的 \(pre_{2,i}\) 都可以拎出来最后算。对于第一个式子，\(f[i](i\ge l)\) 用 \(f[l-1]\)，说明应按左端点递增顺序处理操作，进而常规区间修改。对于第二个式子，相当于是这次 \([l,r]\) 内部所有人对后面的人做 \(pre_{1,j}-pre_{2,j-1}\)（常数，记为 \(t_j\)）的贡献，利用算法本质特征，在每次线段树左边回溯时带上来左边已经更新的 \(t_j\) 的最大值，接下去做右边；对于线段树一个节点代表一个区间的，就先用 \(\text{tag}\) 保存标记，在 pushdown 时做类似性质的操作。
答案就是 \(\max(f[i]+pre_{3,n}-pre_{3,i-1})\)。

1733D2 Zero-One(Hard Version)

sol

加强版：n ≤ 1e7
显然，那些 a[i]=b[i] 的位置作废。用 mis[i] 存储每一个 mismatch 所在的下标。另一个显然的观察是无解当且仅当 mismatch 个数为奇数。
这个题还有一个 Easy Version，启发我们分开考虑 \(x\ge y\) 和 \(x<y\) 的情况。
对于前者，显然就是把所有 mismatch 第一个和最后一个配对、第二个和倒数第二个配对……这样到最后会配对到只剩 4 个，交错配对即可。特判一下只有 2 个 mismatch 的情况。
对于后者，我们可以考虑一个 dp：f[i] 表示 mis[] 的前缀 i，全部变成目标的 mincost。当 i is odd 的时候是变不完的，会有一个剩余。这一个剩余会留给下一个 i（是个偶数）的时候做备选。这启发我们从 i 的奇偶性分类讨论转移。i 为偶数时，从 f[i-2]+x*(mis[i]-mis[i-1]) 和 f[i-1]+y 转移过来；i 为奇数时，从 f[i-1] 和 f[i-2]+x*(mis[i]-mis[i-1]) 转移过来（可以省去 f[i-2]+y 的备选项，因为从 i-1 的转移式可以发现 f[i-1] ≤ f[i-2]+y）。

1654G Snowy Mountain

一棵 \(n(n\le 2*10^5)\) 个点的树，布尔数组 \(l_i\) 表示点 \(i\) 是不是基地，一个点的高度 \(h_i\) 为其到最近的基地的距离。从一个点出发时动能为 0，随后可以下滑或走平地，从 \(u\) 到相邻的 \(v\)：若 \(h_u>h_v\)，则增加 1 动能，若 \(h_u=h_v\)，则减少 1 动能。问从每个点出发、全程动能非负最远可以到的距离。

sol

滑雪下来重力势能做的功是恒定的，我们实际要最大化产生的热能，即滑更多的平地。

结论1（贪心）最优策略为滑到一个海拔最低的“辗转点”，再在这个平台上辗转直到动能耗尽，再由它径直滑到最近的基地。定义“辗转点”为相邻节点中有与它等高的点的点。
证明：当人到达终点时，具有动能 \(w\)，\(w\) 就是完全被浪费的，原因是除掉恒定的那 \(h_u\) 个单位长度，没有浪费的机械能都会转化为一单位热能，即一单位长度，要最小化浪费，就要最低化目标“辗转点”。进一步量化，令 \(h_u,h_v\) 为起始点和目标“辗转点”的高度，\(len\) 表示路径总长度，则根据上面有 \(len=h_u+(h_u-h_v)=2h_u-h_v\)。

现在的任务变为求一个点能到达的最低“辗转点”。

结论2 所有“辗转点”的高度总和为 \(O(n)\) 级别。
证明：

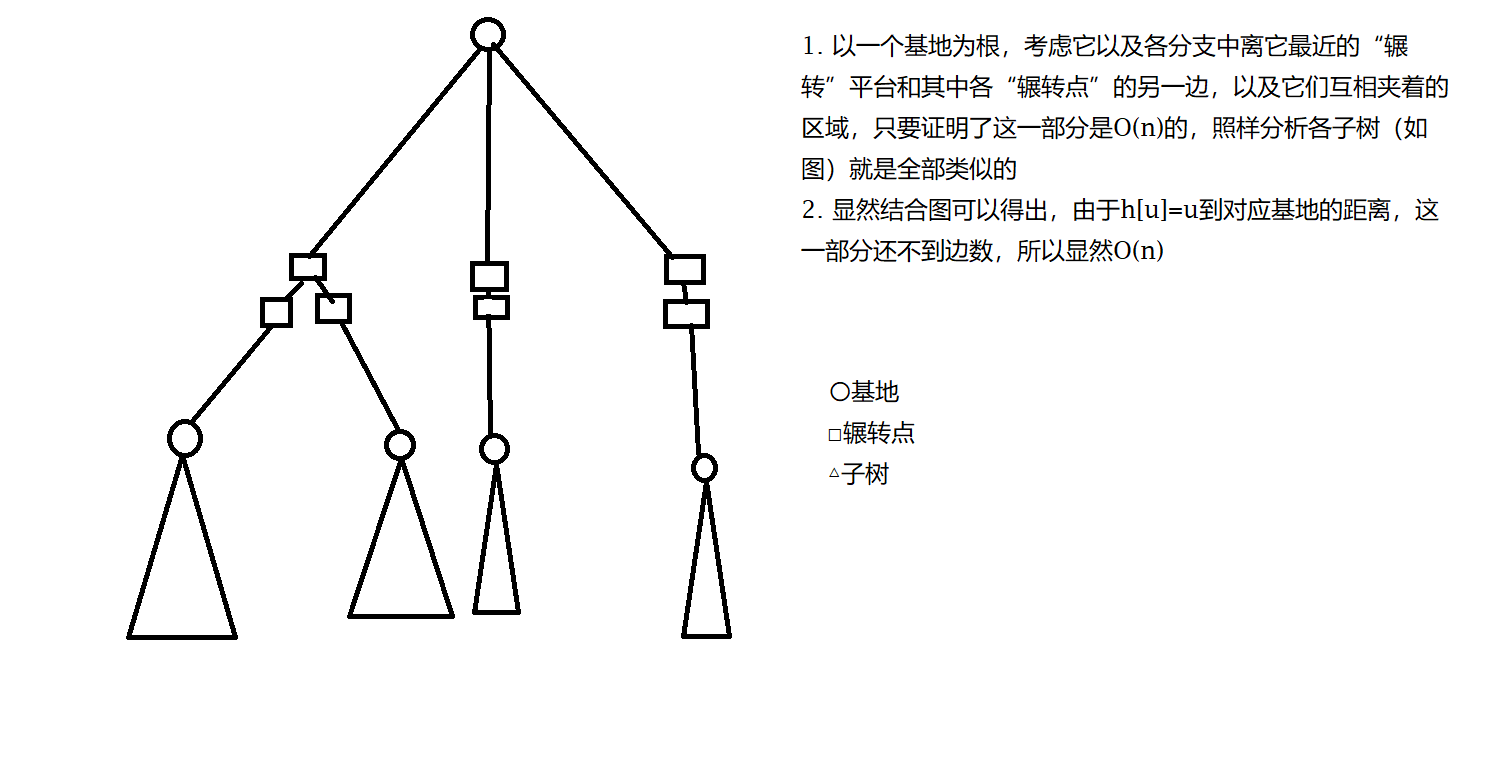
推论 高度不同的“辗转点”数量不超过 \(\sqrt{2n}=O(\sqrt n)\)。（最坏情况下是 \(\sum h=1+2+...\)）

这就是说我们可以暴力枚举辗转平台高度，并看看哪些点可以到达这一高度的辗转点的任意一个，更新它们的答案。
具体地，我们设 \(c_u\) 为 \(u\) 到达任何一个这一高度的辗转点的最小初始动能，则扩展 \(c_u\) 的过程等价于在一个边权为 \(h_u=h_v\to 1\)、\(h_u<h_v\to-1\) 的图上跑多源最短路；这个可以使用分层 bfs，将高度相同的点视作同一层，按高度从小到大处理每一层：在层内部做普通的 bfs（一个点可能会多次入队，但所有点的入度之和是 \(O(n)\) 的），搞完后进行 \(h\to h+1\) 的边的扩展。总时间复杂度 \(O(n\sqrt n)\)。

1278F Cards

有 \(m(m\le 10^9)\) 张牌，其中一张是王牌。现在你执行 \(n(n\le 10^9)\) 次如下操作：洗牌后查看第一张牌是什么。
令 \(x\) 为洗牌后第一张牌为王牌的次数，现在假设洗牌时 \(m!\) 种牌的排列出现的概率均相等，求 \(x^k(k\le 5000)\) 的期望值。

sol

显然一次顶上为王牌概率 \(p=\frac 1m\)。
我们称轮次集合为一种方案中王牌在顶的轮次编号构成的集合。大小为 \(x\) 的轮次集合产生 \(x^k\) 的贡献（概率最后考虑）。
考虑 \(x^k\) 的组合意义为构造一个长 \(k\) 的序列只能从该轮次集合选数的方案数。
从长 \(k\) 序列角度考虑它对包含它的轮次集合们做的总贡献，不难发现贡献只和序列中互异元素的个数 \(t\) 有关，若 \(f_t\) 为这种序列的个数，则存在这种序列的概率为 \((\frac1m)^t\)（也即包含它的轮次集合们被选到的概率总和），因为序列中数本来的意义还是轮次抽到王。容易用 \(O(k^2)\) 的 dp 推出 \(f_t\)。

1239E Turtle

一只乌龟从 \(2 \times n\) 的矩阵 \(a\) 的左上角走到右下角，只能往下或往右，得分等于经过的数字之和，它自动走最大得分的路线，给出一种重排 \(a\) 的方案，使得乌龟的得分最小。

sol

第一步还是分析性质以求转化。性质一是上头一定从左到右逐渐增大，下面一定从左到右逐渐减小，这样总能让乌龟更有可能接触到的是较小数字。性质二是最小的两个数一定分居左上角和右下角，证明可以简单反证。
接下来是重头戏。我们假设乌龟在第 \(x\) 列下来，那么 \(a_{1,1}+...+a_{1,x}+a_{2,x}+...+a_{2,n}=f(x)\) 为乌龟的得分，而列式知 \(f(x+1)-f(x)=a_{1,x+1}-a_{2,x}=g(x)\)，由于 \(a_1\) 递增而 \(a_2\) 递减，所以 \(g(x)\) 递增，所以 \(f(x)\) 是一个先减小后增大的东西（也可以只减小/增大），故唯可能在 \(f(1)\) 或 \(f(n)\) 处取得最大值，这是乌龟的策略。形成了转化，要最小化 \(\max(a_{1,1}+\sum a_2,a_{2,n}+\sum a_1)=a_{1,1}+a_{2,n}+\max(\sum_{i=1}^{n-1}a_{2,i},\sum_{i=2}^n a_{1,i})\)。
这样的好处在于前两项都已知了，后面显然就是一个简单的 01 背包。但是这样过不了，时间空间都太大，用 bitset 可以削减常数和空间，但是空间还是要小心开：bitset<M>f[51][25],from[51][25];

1704E Count Seconds

有一张有唯一零出度点的 DAG，点数为 \(n(n\le 1000)\)，边数为 \(m(m\le 1000)\)，每个点上有 \(a_i(0\le a_i\le 10^9)\) 个球。每一秒取出点集 \(S=\{x|a_x>0\}\)，并对所有 \(x\in S\)，使 \(a_x\gets a_x-1\)，并使 \(\forall y,(x,y)\in {\bf {E}},a_y\gets a_y+1\)。问多少秒之后所有 \(a\) 变为 0？

sol

通过观察发现，一定在某个时刻之后，汇点的 \(a\) 会保持 \(>0\)，最后变成 0. 在这种状态下，由于每秒汇点只输出 1 unit，所以这个状态会持续的时间就是所有最后会到达汇点的球的个数，这个东西的求法就不需要每秒模拟过程，而可以按照拓扑顺序将每个点的 \(a\) 全部加给出边的点，得到的 \(a_{汇}\) 就是它。
那么什么时候可以到达这样的状态？考虑不处于这种状态的缘故是：点的分布一段是 \(a>0\)，一段是 \(a=0\)……所以只需要使 \(a>0\) 的部分黏在一起就好了。每次至少填充一个点，而 \(a=0\) 的点的长度不超过 \(n\)，所以暴力模拟前 \(n\) 秒后得到的状态一定就是上述状态；当然也可能还没到 \(n\) 秒就全 0 了。

1749E Cactus Wall

sol

观察到我们只需要求一条从左贯穿到右的 Cactus 路径即可，路径的连接方式是对角线方向。不难想到建立有向图，\((u\to v)\) 的边权为 \([v处没有cactus]\)。需要小心的是，和原 cactus 的位置相邻的位置应避免纳入考虑。从超级源点向超级汇点跑 dij，记录方案即可。*2400

Others

1364E X-OR

【交互题】长度为 \(n\) 的排列 \(P\)，其值域为 \([0,n-1]\)，进行不超过 4269 次询问后输出排列。询问格式：? a b 得到 \(P_a|P_b\)（按位或）。

sol

发现找到 \(0\) 的坐标是突破口，因为这样一来询问 \(0|a_i=a_i\)。
做一个随机的排列 \(z_n\)。
初始时 \(x=z_1,y=z_2\)，相当于随机了两个位置。
接下来枚举 \(z_i(i\ge 3)\)，想办法依赖之调整 \(x,y\)，使最终 \(x,y\) 中有一个是 \(0\)。

假如 \(a_x|a_y>a_y|a_z\)，则 \(a_x\) 不可能是 \(0\)，\(x\gets z\)；
假如 \(a_x|a_y=a_y|a_z\)，则 \(a_y\) 不可能是 \(0\)，\(y\gets z\)。

最终的 \(x,y\) 中有一个满足对应 \(0\)（预期是这样）。

再遍历一遍 \(z\)，如果 \(a_x|a_z\ne a_y|a_z\)，则可以排除掉 \(x,y\) 中的一个，并 break。预期这一部分询问数不会超过 \(173\)。
/随机化

1642E Anonymity Is Important

给你关于 01 数组 \(a_n(n\le 2\times 10^5)\) 的 \(q(q\le 2\times 10^5)\) 条在线的信息，请你确定一个

• 0 l r 0：\(\forall l\le i\le r,a_i=0\)
• 0 l r 1：\(\exists l\le i\le r,a_i=1\)
• 1 x：查询 \(a_i\)，若为0输出 NO，若为1输出 YES，若暂且确定不了输出 N/A。

sol

一句话题解：主席树+二分。

---

只可能是一个 0 ... ... 1 的询问可以在某时刻发现区间内只有一个没被覆盖的位置从而确定该时刻以后这个位置是1.
考虑离线所有0号询问，把每一时刻的线段树中覆盖的状态用主席树维护，对于每个 0 ... ... 1 二分最早在【什么时候】可以确定其中的【哪一个位置】是1。【】中是需要记录的。
注意主席树中查找空位置下标时，可能这个点压根是空的，用 if(!k){if(r>=L&&r<=R)return r;if(l>=L&&l<=R)return l;return L;} 返回任意的一个。
submission *2200

Maths and Number Theory

1654D Potion Brewing Class

已知 \(n-1(n\le 2\cdot 10^5)\) 个 \(a_i:a_j=x_i:y_i(x_i,y_i\le n)\) 的关系式，请你确定整数数组 \(a\) 的 \(\sum a_i\) 最小是多少？（模 998244353）

sol

不应该想不到。令 \(a_1=1\)，将各点写成 \(V=p_1e^1p_2e^2...p_ke^k\) 的质数幂形式，其中 \(p_1...p_k\) 是 \(\le n\) 的质数集，\(e_i\) 可正可负可为0. 分母的 lcm 是 \(a_1\) 的最小值，所以对每个 \(p_i\) 记录 \(e_i<0\) 时的 \(\max(-e_i)\)，最后乘上它即可。由于质数为 \(O(\log n)\) 个，所以经过一条边修改 \(O(\log n)\) 次，维护 \(V\) 以及 \(e_i\) 即可。

ARC(exa2019)D Modulo Operations

给你 \(x\le 10^5\) 和互不相同的数列 \(a_n(n\le 200)\)，求所有 \(a\) 的排列的 x%a[1]%a[2]%...%a[n] 的和。

sol

1. 将 \(a\) 升序排序
2. 设 f[i][j] 表示 \(a[1\sim i]\) 的答案
3. f[i][j]=f[i-1][j%a[i]]+(i-1)*f[i-1][j]，考虑是先 %a[i] 还是后模，如果是后模就可以插到 1~i-1 之前

GYM103371J

数轴上每个点有一个颜色；当 \(c_i=c_{i+T}(T>0)\) 时，\(T\) 为一个正周期。
给出数轴上 \(n(n\le 50)\) 个点的位置 \(x_i(|x_i|\le 10^9)\) 和颜色 \(a_i(a_i\le 100)\)，问最小正周期不可能是多少。输出答案的数量和加和。

sol

1. 不可能是周期的T可以直接加入答案
2. 可能是正周期但不可能是最小正周期的
   如何判断：
   首先，这样的正周期一定<=n，不然区间[u,u+t)中一定存在一个位置为空，在这个空位置一定可以填一个异于区间内任何已有颜色的颜色，从而使t为最小正周期
   将每个(xi,ai)放到(xi%T,ai)，那么[0,T)（代表了一个周期单元）内就会有一些位置颜色固定了
   （1）如果存在一个颜色没有被固定，那么同上就一定是一个合法的周期
   （2）如果所有颜色都固定了，那么考察是否有j<T使j为周期。具体地，如果j不整除i，那么无需考虑这个j，不证自明；否则，暴力判断即可。
   submission

1332E Height All the Same

对于一个 \(n*m\) 的矩阵，可以执行任意次操作，每一次操作任选下列两种之一：

• 将一对相邻元素同 \(+1\)
• 将一个元素 \(+2\)

有多少个矩阵 \(a\) 同时满足：

• \(L\le a_{i,j}\le R\)
• 可以使最终所有元素相等

\(n,m,L,R\le 10^9\)

sol

容易看出问题的本质在于奇偶性。关键在发现：任意一对矩阵中的偶数都可以通过修改一条“路径”（类似曼哈顿距离）同时改变其奇偶性，而不改变矩阵中其他元素奇偶性。所以问题转为求【含偶数的个数是偶数或奇数的个数是偶数的矩阵数量】。

当 \(2\nmid n\)，必然成立。
当 \(2\mid n\)，显然需要偶/奇数的个数是偶数，\(\sum_{0\le i\le nm,2|i}{n\choose i}p^iq^{nm-i}\)，这个类似于二项式定理的一半，通过 \((p+q)^{nm}+(p-q)^{nm}\) 消去奇数项。

Games

1628D Game on Sum

sol

1704F Colouring Game

一个长为 \(n\) 的 RB 双色序列，Alice 每次可以选一对包含至少一个 R 的相邻位置，改成白色，Bob 每次可以选一对包含至少一个 B 的相邻位置，改成白色，问两个人都采用最优策略，谁会赢？\(n\le 5\cdot 10^5\)

sol

最优策略：双方都取 RB/BR，取完之后尽量拖延时间，每次选一个 _W/W_(_表示自己的颜色)。
只需要知道前一部分谁会最后没办法取 RB/BR。会出现若干个隔开的 ..RBRBR.. 这样的交错段，故 SG=每一段的 SG 异或起来。每一段的游戏描述为：每次取任意一个相邻位置，不能取的输，所以 \(SG(i)=\text{mex}_{j=0}^{i-2}SG(j)\oplus SG(i-2-j)\)。打表发现从 53 开始出现长为 34 的循环节，所以只需要暴力算前面的 SG(0) 到 SG(86)，后面拷贝。