JOISC2023 简单题整理

D1T1 currencies

忘了，比较水，主席树，略。

D1T3 passport

\(n\) 个国家排成一排，一个人如果在国家 \(x\)，他可以选择获得一张通行证，作用范围为 \([l_x,r_x]\) 这些国家（\(l_x\le x\le r_x\)）。有 \(m\) 个独立的人，分别从 \(X_1,X_2,...,X_m\) 出发，问每个人想要周游 \(n\) 国最少需要取几张通行证。\(n,m\le 10^5\)

线段树优化建图的提示非常明显，但距离做出这题似乎还是有难度。这个所求在一般图上似乎是一个 NP 问题，于是考虑此题的特殊性：区间性。我们发现，要想周游列国，只需要 \(1\) 和 \(n\) 是可达的就行了。于是我们要在这张线段树优化建图上从 \(X_i\) 到达 \(1\) 和 \(n\)，两方最短路的和。但是明显会有共用通行证的一段，似乎又变得不可做了，但冷静分析即可发现，如果共用，那只可能共用开始的一段，后面就分道扬镳了。

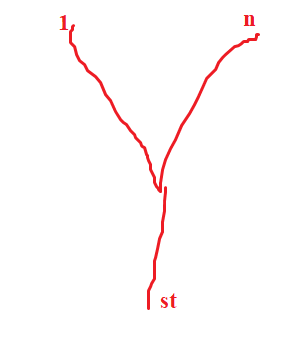
【套路】求解“Y”形最短路的方法：先求 \(dis_{1,i}\)、\(dis_{i,n}\)，然后初始化 \(dis_i\) 为 \(dis_{1,i}+dis_{i,n}\)，并将 \(n\) 个点统统入 priority_queue，跑 Dij，求得的 \(dis_{1..n}\) 即为每个 \(st\) 对应的“Y”形最短路。
解释：如果记“Y”形最短路的分叉处为 \(o\)，则 \(o\) 处的 \(dis\) 即为 \(dis_{1,o}+dis_{o,n}\)，它再松弛 \(o\sim st\) 的一段即得答案。

D2T2 council

有一个 \(n\times m(n\le 3\times 10^5,m\le 20)\) 的 01 矩阵，对于 \(i=1\sim n\)，你需要删除第 \(i\) 行以及除 \(i\) 以外的一行，使得留下的矩阵的包含 \(\ge \lfloor\frac n2\rfloor\) 个 1 的列数尽可能大。输出最大列数。（注意: \(n\) 没变；并没有真删）

考虑如果一列有 \(\ge n+2\) 个 1 则必选，如果有 \(n+1\) 个 1 则若 \(a_{i,j}=0\) 则第 \(j\) 列必选，否则要求 \(a_{k,j}=0\)，如果有 \(n\) 个 \(1\) 并且 \(a_{i,j}=0\) 则要求 \(a_{k,j}=0\)，其他情况都不可能选。然后看在所有 \(k\ne i\) 中能满足最多要求的是哪个 \(k\)，要求的就是最多能够满足的要求数。换句话说，如果设 \(a'_i\) 为第 \(i\) 行构成的二进制数取反的结果，那么要求 \(\max_{k\ne i}popcnt(a'_k\& c_i)\)，其中 \(c_i\) 为“需要满足的要求”。
不难将问题转化为：（后缀是类似的）

有一个数组 \(A\)，对每个前缀 \(i\)，查询一个数 \(x\)，需要回答 \(\max_{j\in [1,i]}popcnt(A_j\& x)\)。

一个暴力的想法是枚举 \(x\) 的子集，然后看 \(A[1,j]\) 中是否存在一个数是该子集的超集，但是复杂度爆炸呀！那肯定是 FWT 了，怎么 FWT 呢？我们肯定不能每轮都做一次 FWT，那就离线地搞，那就有两个属性：时间，和 popcount。希望对于每个数，找到一个首次出现时间最小的超集。然后再做一遍 FWTOR，得到每个数的“首次可用时间”最小的子集。那时间一维肯定要放到值域里了，popcount 就得暴力枚举了。具体来说，先把 \(g(A_i)\gets i\)，然后对 \(g\) 求一遍高位后缀 min。接着将 \(f(ppc(i),i)\gets g(i)\)，然后对 \(f(i,*)\) 的 \(*\) 维求一遍高维前缀 min。最后对每个询问，暴力枚举 \(ppc\)，查看 \(f(ppc,x)\) 是否 \(<i\) 即可，若是则用 \(ppc\) 更新答案。

D3T3 tourism

给定一棵树，\(q\) 次查询区间 \(C_{l_i}...C_{r_i}\) 的斯坦纳树的点数。\(n,q\le 10^5\)（莫队+set会TLE）

其实一点也不难，DS 套路见少了。
【套路】离线区间型问题，除了（1）分治（整体贰分）外，常常（2）将区间存在一个端点处（不妨设是右端点），然后在扫前缀的过程中，努力留下“修改时间”这一维的痕迹，其方式或是通过建立线段树以下标的一段区间体现，或是将时间戳打到对象上然后进行值域上的统计……
本题，不可能以下标的一段区间体现这个东西，因为题目给我们了一棵树不能搁那儿不管；考虑将时间戳打到树上去。具体来说，到达 \(r\) 时，我们所求的斯坦纳树应该满足它的每一条边的最后一次覆盖时间都 \(\ge l\)，一次覆盖是指对于相邻两个点 \(C_{i-1},C_i\)，将其路径上的所有边都打上 \(i-1\) 的标记。反过来，如果一条边的最后一次覆盖时间 \(\ge l\)，它一定属于所求的斯坦纳树。
现在问题转化为了 dfn 上区间赋值、区间查询 \(\ge l\) 的数的个数。不难想到可以不用树剖—线段树，而用树剖—set—BIT，即对于树剖欲修改的一段 dfn 区间 \([x,y]\)，将 set<pair<pair<int,int>,int> > 中 \(\subseteq[x,y]\) 的所有区间（以及与之有交但不完全包含的，这种要先一分为二）给删了（暴力删），然后插入一段 \((x,y,i-1)\)，并同时在 BIT 上做相应更新。暴力删的复杂度是对的的分析无须赘述。

D4T3 travel

转头次数为 log 的观察+倍增，比较水，略。