鞅的停时定理随笔

鞅的核心性质

1. 对于一个随机过程 \(A_0,A_1,...,A_t\)，\(\forall n\in[0,t)\)，\(E(\Phi(A_{n+1})-\Phi(A_n)\mid A_0,A_1,...,A_n)=-1\)。\(\mid\) 后表示 \(A_0...A_n\) 已经确定时来推。
2. \(E(t)=\Phi(A_0)-\Phi(A_t)\)，用这个等式来解决问题，求出初始和末了局面的 \(\Phi\) 即可。

势能函数 \(\Phi(A)\)
对于局面 \(A\)，它的要素（变化对象）可能是若干个个体，对于个体 \(x\) 设其势能函数为 \(f(x)\)，则 \(\Phi(A)=\sum_{x\in A}f(x)\)。\(f(x)\) 通常较宽松，在满足一定条件下具体取值可以自定义，如：（1）可强化：可以将双变量递推式强化成单变量递推式，可以将必要条件强化成充要条件（直接拿当前式子的必要条件来继续往后推）；（2）取值：通常只能推出递推式而不能知道边界值如 \(f(0)\)，此时一般可以令 \(f(0)=0\)。

势能函数递推式的推导方法
大体上是：

1. 设出 \(f\) 的含义，\(\Phi(A)=\sum f(a)\)。
2. 列出一次操作（变化）前后（\(A_n,A_{n+1}\)）的变化量 \(E(\Phi(A_{n+1})-\Phi(A_n))\)，令它 \(=-1\)（具体就是把 \(\Phi\) 的表达式带进去然后从 \(A_n\) 推到 \(A_{n+1}\) 的表达式，然后就有 \(f(a),f(a+1),f(a-1)\) 等的一些递推关系出来了）。化简时需要结合代数式对称性等多种手段。
3. 令初始值等于 \(0\) 等，求出 \(f(a)\) 关于 \(a\) 的表达式，或根据初始值开始 dp 求出 \(\forall a,f(a)\)。
4. 按照 \(\Phi=\sum f\) 求出初始和末了局面的 \(\Phi\)，用停时定理求出答案

【例】Snuke and Biscuits

第 \(i\) 个人有 \(a_i\) 个饼干,\(\sum a_i\le 10^6\)，每局随机选一块饼，随机抛给另一个人，当所有饼都集中到一个人手中时终止，求终止时的期望轮数。

设 \(\Phi(A_n)=\sum f(a_{n,i})\)。记 \(m=\sum a_i\)。
\(E(\Phi(A_{n+1})-\Phi(A_{n}))=-1\)
\((\sum f(a_{n,i}))-1=\sum_{i\ne j}{a_i\over m(n-1)}(f(a_{n,i}+1)+f(a_{n,j}-1)+\sum_{k\ne i,k\ne j}f(a_{n,k}))\)
\(\sum_{i\ne j}{a_i\over m(n-1)}f(a_{n,i}+1)=\sum_i {a_i\over m}(f(a_{n,i}+1)\)
\(\sum_{i\ne j}{a_i\over m(n-1)}f(a_{n,j}-1)=\sum_{i}\sum_{j\ne i}{a_j\over m(n-1)}f(a_{n,i}-1)=\sum_{i}{m-a_i\over m(n-1)}f(a_{n,i}-1)\)
\(\sum_{i\ne j}{a_i\over m(n-1)}\sum_{k\ne i,k\ne j}f(a_{n,k})=\sum_{i\ne k}{a_i(n-2)\over m(n-1)}f(a_{n,k})=\sum_k{(m-a_k)(n-2)\over m(n-1)}f(a_{n,k})\)
代入，并将等是左侧的 \(-1\) 挪进括号，可知 \(\sum_i f(a_{n,i})-{a_{n,i}\over m}=\sum_{i}({a_i\over m}(f(a_{n,i}+1)+{m-a_i\over m(n-1)}f(a_{n,i}-1)+{(m-a_i)(n-2)\over m(n-1)}f(a_{n,i}))\)
将 \(a_{n,i}\) 看成 \(x\)，再将上式强化成 \(f(a_{n,i})-{a_{n,i}\over m}=({a_i\over m}(f(a_{n,i}+1)+{m-a_i\over m(n-1)}f(a_{n,i}-1)+{(m-a_i)(n-2)\over m(n-1)}f(a_{n,i}))\)，就可得到递推式，进行 dp：

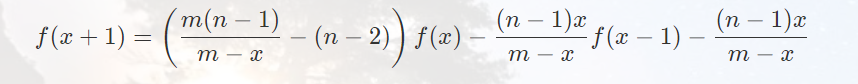
则 \(E(t)=\Phi(A_0)-\Phi(A_t)=-f(m)+\sum f(a_i)\)。