状压 DP(ZR)
[PKUSC2018]最大前缀和
从部分分出发考察性质,“满足 a 中至多一个负数”怎么做?好吧这个很简单,但是它提醒我们从负数的 POV 考虑。不难发现,最大前缀和的结束为止一定是某个负数之前,而这个位置 \(i\) 作为最大前缀和的充要条件就是 \(\forall j\in [1,i]\),前缀和 \(j\) 都 \(\le\) 前缀和 \(i\),\(forall j\in (i,n]\),前缀和 \(j\) 都 \(<\) 前缀和 \(i\)。不难发现,就是 \([1,i]\) 的每一个后缀和 \(\ge 0\),\([i+1,n]\) 的每一个前缀和 \(<0\)。
这就是分成两部分,一部分满足条件一,另一部分满足条件二的意思啊!显然的状压 DP。设 \(f(s),g(s)\) 分别表示选出并排列 \(s\),使得满足前者和后者的方案数。
最后的统计答案,发现有点小小问题,就是如果第一个数是负数,就会统计不到,所以我们令 \(f(0)=g(0)=1\),然后枚举第一个数,这样实在不行可以选空集。
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,ans,a[25],f[1<<20],g[1<<20];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=0;i<n;i++)if(a[i+1]>=0)f[1<<i]=1;else g[1<<i]=1;
for(int s=0;s<(1<<n);s++){
if(s==(s&-s))continue;
int sum=0;
for(int i=0;i<n;i++)if(s>>i&1){
sum+=a[i+1];
add(f[s],f[s^(1<<i)]);
}
if(sum<0)f[s]=0;
}
for(int s=0;s<(1<<n);s++){
if(s==(s&-s))continue;
int sum=0;
for(int i=0;i<n;i++)if(s>>i&1){
sum+=a[i+1];
add(g[s],g[s^(1<<i)]);
}
if(sum>=0)g[s]=0;
}
f[0]=g[0]=1;
for(int i=1;i<=n;i++){
int U=((1<<n)-1)^(1<<(i-1));
for(int s=0;s<(1<<n);s++)if((s&U)==s){
int sum=a[i];
for(int j=0;j<n;j++)if(s>>j&1)sum+=a[j+1];
sum=(sum%mod+mod)%mod;
add(ans,1ll*f[s]*g[U^s]%mod*sum%mod);
}
}
cout<<ans;
}
[PKUWC2018]随机算法
【套路】独立集 DP 时,重点观察独立集内节点的邻居集合,每加入一个点到独立集,就把它和它的邻居一起加入状态,而独立集自身通过大小刻画即可。
设 \(f(i,s)\) 表示独立集大小为 \(i\),独立集中点连同其所有邻居占据集合 \(s\),的方案数。考虑下一个 加入独立集 的点,它应该和 \(s\) 无交集,这种情况下可以转移到 f(i+1,s|(1<<k-1)|adj[k]),转移系数是 \(A_{n-1-|s|}^{|s\cup adj_k|-|s|}\)。
算出最大独立集大小 \(mx\),答案就是 \(f(mx,U)\)。
[PKUWC2018]随机游走
什么是 Min-Max 容斥?
\(\min_{i\in S} a_i=\sum_{T\subseteq S}(-1)^{\color{red}{|T|+1}}\max_{i\in T}a_i\)
\(\max_{i\in S} a_i=\sum_{T\subseteq S}(-1)^{\color{red}{|T|+1}}\min_{i\in T}a_i\)
在本题中,\(a_i\) 就是集合中各点的到达时间,最晚到达时间是所求,但最早到达时间更容易计算。
为什么最早到达时间更容易 DP 呢?这是因为如果设 \(f(i,s)\) 表示从 \(i\) 去 \(s\) 中所有点至少一次的期望步数,就不知道边界在哪,但如果设成去到 \(s\) 中最近一点的期望步数,边界就是 \(s\) 中点自身的 \(f(i)=0\)。(当然我也不确定是不是那样一定不可做,因为貌似也没错,但是容斥后做肯定可做)

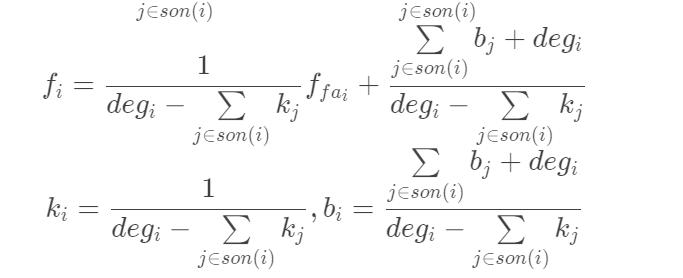
考虑到根节点(起点 \(x\))不能从“父亲”转移,所以转移式没有 "fa" 一项,因此 \(f_{rt}=b_{rt}\)。Min-Max 部分用高维前缀和加速。
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,q,rt,k[20],b[20],g[1<<18];
vector<int>G[20];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline int qp(int a,int b){int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;return c;}
void dfs(int x,int p,int s){
int sk=0,sb=0;
for(int y:G[x])if(y^p){
dfs(y,x,s);
add(sk,k[y]),add(sb,b[y]);
}
if(s>>(x-1)&1)k[x]=b[x]=0;
else k[x]=qp(((int)G[x].size()+mod-sk)%mod,mod-2),b[x]=1ll*(sb+G[x].size())*k[x]%mod;
}
int main(){
cin>>n>>q>>rt;
for(int i=1,u,v;i<n;i++)
cin>>u>>v,G[u].emplace_back(v),G[v].emplace_back(u);
for(int s=1;s<(1<<n);s++){
dfs(rt,0,s);
g[s]=b[rt]*(__builtin_popcount(s)&1?1ll:mod-1ll)%mod;
}
for(int w=1;w<(1<<n);w<<=1)
for(int i=0;i<(1<<n);i+=w<<1)
for(int j=0;j<w;j++)
add(g[i+j+w],g[i+j]);
while(q--){
int K,tmp,s=0;
cin>>K;
while(K--)cin>>tmp,s|=1<<(tmp-1);
cout<<g[s]<<'\n';
}
}
[SNOI2017]遗失的答案
考虑到题意其实很简单,我们只需要对于每一个 L 的质因子,都存在一个所选数顶上界,且存在一个所选数顶下界。
考虑到 \(L\le 10^8\) 质因子数目不超过 \(8\),可以设计一个 \(2^{2\times 8}\) 的状态,表示每个质因子是否顶 L 的上界和是否顶 G 的下界。
需要一些数(须是 1~N 且是 L 的因子)的状态 or 起来是全集,不好做,想反演,or 起来是 \(S\) 的子集呢?那么如果所有满足条件的数中,状态是 \(S\) 的子集的有 \(c\) 个,答案就是 \(g(S)=2^c\)。\(f(S)\) 通过二项式反演求得。
考虑“必须选 \(x\)” 的限制,因此对于 \(x\subseteq S\) \(g(S)=\frac{2^c}2\)(有一半是选 \(x\) 的,一半不选),而 \(x\not\subseteq S\),就必定没选 \(x\),\(g(S)=0\);二项式反演部分可以通过暴力完成,因为只需要枚举 \(x\) 的超集,总共是 \(O(3^n)\) 的。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int mod=1e9+7;
int n,q,G,L,siz,h[1<<16],ppc[1<<16],_2[100005];
vector<int>P,cL,cG;
map<int,int>mp;
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline void work(int x){
if(x%G!=0||x>n)return;
int st=0,o=1,i=0;
for(int p:P){
int cnt=0;
while(x%p==0)x/=p,cnt++;
st|=o*(cnt==cL[i]),st|=(o<<1)*(cnt==cG[i]);
o<<=2,i++;
}
h[st]++;
}
int main(){
n=read(),G=read(),L=read(),q=read();
int tmp=L;
for(int i=2;i*i<=tmp;i++)if(tmp%i==0){
while(tmp%i==0)tmp/=i;
P.emplace_back(i);
}
if(tmp>1)P.emplace_back(tmp);
siz=P.size();
for(int p:P){
tmp=L;
int cnt=0;
while(tmp%p==0)tmp/=p,cnt++;
cL.emplace_back(cnt);
cnt=0,tmp=G;
while(tmp%p==0)tmp/=p,cnt++;
cG.emplace_back(cnt);
}
for(int i=1;i*i<=L;i++)if(L%i==0){
work(i);
if(i*i!=L)work(L/i);
}
siz*=2;
for(int w=1;w<(1<<siz);w<<=1)
for(int i=0;i<(1<<siz);i+=w<<1)
for(int j=0;j<w;j++)
h[i+j+w]+=h[i+j];
for(int i=1;i<(1<<siz);i++)ppc[i]=ppc[i-(i&-i)]+1;
_2[0]=1; for(int i=1;i<=1e5;i++)_2[i]=_2[i-1]*2%mod;
for(int x;q--;){
x=read();
if(L%x!=0||x%G!=0||x>n){puts("0");continue;}
int st=0,o=1,i=0,xx=x;
for(int p:P){
int cnt=0;
while(xx%p==0)xx/=p,cnt++;
st|=o*(cnt==cL[i]),st|=(o<<1)*(cnt==cG[i]);
o<<=2,i++;
}
x=st;
if(mp[x])cout<<mp[x]<<'\n';
else {
int ans=0;
for(int t=((1<<siz)-1)^x,St=t;~t;t=(t-1)&St){
int s=((1<<siz)-1)^t;
if(h[s])add(ans,((siz-ppc[s])&1?mod-1ll:1ll)*_2[h[s]-1]%mod);
if(!t)break;
}
cout<<(mp[x]=ans)<<'\n';
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号