ACSX: Jan&Feb, 2023
飞花
有 \(n(n\le 2\times 10^5)\) 张卡牌,正面 \(a_i\),反面 \(b_i\),所有 \(1\le a_i,b_i\le 2n\) 且互不相同。
你可以选择翻任意张卡牌,翻完后可不耗代价任意重排,问最少翻多少张牌,使得最后有 \(a_1<a_2<a_3<...<a_n\) 且 \(b_1>b_2>b_3>...>b_n\)?
首先有个小性质一定得把握到,这是突破口:若存在 \(a_i>n,b_i>n\) 则一定无解(原因是若存在这样的一组则必存在一组都小于等于 n 的,这两个不可能形成答案的pattern)
有了这个那就是说每一张牌都是一个在 [1,n] 一个在 [n+1,2n],那么都好做了。这样显然按照较小面递增的顺序排列就需要得到两个降序列,第一个不再翻,第二个再翻一次接到右边。也就是问题转化为一个数组 \(\{A_n\}\),有两个初始为正无穷的降序列,每个元素放到0序列末端需要支付0/1的代价,放到1序列末端需要支付0/1的代价(钦定0序列是后来不再翻的,1序列是后来再翻的),需要保证是降序列,最小代价是多少。
显然的 DP,设 \(f(i,j,0/1)\) 表示到 \(i\),\(j\) 为“另一个序列”的末数值,\(A_i\) 放到哪个序列,的最小代价。
if(a[i+1]<a[i]) f[i+1][x][0]<----f[i][x][0]+[a[i+1]已翻转],f[i+1][x][1]<---f[i][x][1]+[a[i+1]未翻转]
f[i+1][a[i]][0]<----f[i][x>a[i+1]][1]+[a[i+1]已翻转],f[i+1][a[i]][1]<----f[i][x>a[i+1]][0]+[a[i+1]未翻转]
使用线段树维护转移。注意如果 a[i+1]>a[i] 的话是要清空线段树的(全设成INF),然后线段树是单点修改查区间最小值。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5,INF=1e9+7;
int n,a[N<<1],st[N];
struct SGT {//range [1,n+1]
int t[N<<2],tag[N<<2],cl[N<<2];
void build(int l,int r,int k){
if(l==r){t[k]=INF;return;}
int mid=l+r>>1;
build(l,mid,k<<1),build(mid+1,r,k<<1|1);
pushup(k);
}
void pushup(int k){t[k]=min(t[k<<1],t[k<<1|1]);}
void pushdown(int k){
if(cl[k]){
t[k<<1]=t[k<<1|1]=INF;
tag[k<<1]=tag[k<<1|1]=0;
cl[k<<1]=cl[k<<1|1]=1;
cl[k]=0;
}
if(tag[k]){
tag[k<<1]+=tag[k],tag[k<<1|1]+=tag[k];
t[k<<1]+=tag[k],t[k<<1|1]+=tag[k];
tag[k]=0;
}
}
int ask(int L,int R,int l,int r,int k){
if(L<=l&&r<=R)return t[k];
pushdown(k);
int mid=l+r>>1,ret=INF;
if(L<=mid)ret=ask(L,R,l,mid,k<<1);
if(R>mid)ret=min(ret,ask(L,R,mid+1,r,k<<1|1));
return ret;
}
void chg(int p,int v,int l,int r,int k){
if(l==r){t[k]=min(t[k],v);return;}
pushdown(k);
int mid=l+r>>1;
if(p<=mid)chg(p,v,l,mid,k<<1);
else chg(p,v,mid+1,r,k<<1|1);
pushup(k);
}
}T[2];
int main(){
freopen("flower.in","r",stdin);freopen("flower.out","w",stdout);
scanf("%d",&n);
for(int i=1,x,y;i<=n;i++){
scanf("%d%d",&x,&y);
if(x<=n&&y<=n)puts("-1"),exit(0);
if(x<y)a[x]=y-n,st[x]=0;
else a[y]=x-n,st[y]=1;
}
T[0].build(1,n+1,1),T[1].build(1,n+1,1);
T[0].chg(n+1,st[1],1,n+1,1),T[1].chg(n+1,!st[1],1,n+1,1);
for(int i=1;i<=n;i++){
int tmp1=T[1].ask(a[i+1]+1,n+1,1,n+1,1)+st[i+1];
int tmp2=T[0].ask(a[i+1]+1,n+1,1,n+1,1)+!st[i+1];
if(a[i+1]<a[i])T[0].tag[1]+=st[i+1],T[1].tag[1]+=!st[i+1];
else T[0].cl[1]=T[1].cl[1]=1;
T[0].chg(a[i],tmp1,1,n+1,1);
T[1].chg(a[i],tmp2,1,n+1,1);
}
int o=min(T[0].t[1],T[1].t[1]);
cout<<(o>=INF?-1:o)<<'\n';
}
幻想
有 \(n(n\le 40)\) 种面额 \(a_1...a_n\),满足 \(a_i|a_{i+1}\),每种面额无数张,要凑出 \(m(m\le 10^{18})\),求方案数。
容易看出是 DP 题,于是试图发现子问题。如果我们放 \(t\) 张 \(a_n\) 的话,还剩下 \(m-t\cdot a_n\),而如果再放 \(s\) 张 \(a_{n-1}\) 的话,还剩下 \(m-t\cdot a_n-s\cdot a_{n-1}=m-\frac{a_n}{a_{n-1}}\cdot t+s)a_{n-1}\),于是我们发现命令前 \(i\) 个数凑出的数一定可以表示成 \(m-t\cdot a_{i+1}\) 的形式,为了和题解保持一致,表示成 m%a[i+1]+x·a[i+1] 的形式。
转移:
设f(i,x)表示用前i凑出m%a[i+1]+x·a[i+1],枚举a[i]用了j个,令m%a[i+1]+x·a[i+1]-j·a[i]=m%a[i]+y·a[i],得 y=(m%a[i+1]+j*a[i+1]-m%a[i])/a[i]-j
因此 f(i,x)=∑{j>=0}f(i-1,y=...),可以观察到本质上就是对f(i-1)求了个前缀和,但是前缀和的那个下标很大很大,让我们想到了拉格朗日插值,发现由于带“%”的都是常数,所以本质上f(i,x)就是一个常函数做了i-1次前缀和的i-1次多项式,要维护n+1个点值,就完了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e6+3;
int n,f[45][45],pre[45],suf[45],jc[45],ijc[45];
ll m,a[45];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
int lag(int x,int y[]){
int ret=0;
pre[0]=x,suf[n]=(x-n+mod)%mod;
for(int i=1;i<=n;i++)pre[i]=1ll*pre[i-1]*((x-i+mod)%mod)%mod;
for(int i=n-1;~i;i--)suf[i]=1ll*suf[i+1]*((x-i+mod)%mod)%mod;
for(int i=0;i<=n;i++)add(ret,1ll*y[i]*(i?pre[i-1]:1)%mod*(i==n?1:suf[i+1])%mod*ijc[i]%mod*ijc[n-i]%mod*((n-i&1)?mod-1:1)%mod);
return ret;
}
inline int qp(int a,int b){
int c=1;
for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
return c;
}
int main(){
freopen("fantasy.in","r",stdin);freopen("fantasy.out","w",stdout);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
if(m%a[1]!=0)puts("0"),exit(0);
else if(n==1)puts("1"),exit(0);
jc[0]=1;for(int i=1;i<=n;i++)jc[i]=1ll*i*jc[i-1]%mod;
for(int i=0;i<=n;i++)ijc[i]=qp(jc[i],mod-2);
for(int i=0;i<=n;i++)f[1][i]=1;
for(int i=2;i<n;i++){
for(int j=1;j<=n;j++)add(f[i-1][j],f[i-1][j-1]);
for(int j=0;j<=n;j++){
f[i][j]=lag((((m%a[i+1]+j*a[i+1]-m%a[i])/a[i])%mod+mod)%mod,f[i-1]);
}
}
for(int i=1;i<=n;i++)add(f[n-1][i],f[n-1][i-1]);
cout<<lag((m/a[n])%mod,f[n-1]);
}
特立独行的图
一个序列 \(\{a_n\}\),\(\max_{i,j}|a_i-a_j|\le L\),\(\forall i\ne j,a_i\ne a_j\),两点 \(i,j\) 有边当且仅当 \(|a_i-a_j|\ge \frac L 2\),现给出无向图,试构造合法的偶数 \(L(L\le 2\times 10^9\) 和序列 \(a\)。
考虑到极差 \(\le L\),以及 \(L/2\) 的限制,将 \(a\) 的值域定在 \([-L/2,L/2]\),不难发现同号的点之间没有边。
当不存在 0 时,是一个二分图,染色以分出正负两部分。负数越小,度数约大,正数约大,度数越大。因此将度数排序,即可实现对点的数值大小排序。
考虑从小到大枚举正数,并给它连接的负数分配数值,贪心地尽量分小的,细节不多。
当存在 0 时,可能存在唯一一个三元环,我们把它找到,另外两个点必须恰好是 \(±L\);也可能不存在,但是只要跟 0 连边的就是 \(±L\);0 的度数一定是三个点中最小的,据此钦定其为 0 即可.
L 取 2e9 就好。
玩游戏
https://www.cnblogs.com/hzoi-DeepinC/p/12844282.html
拿钱了
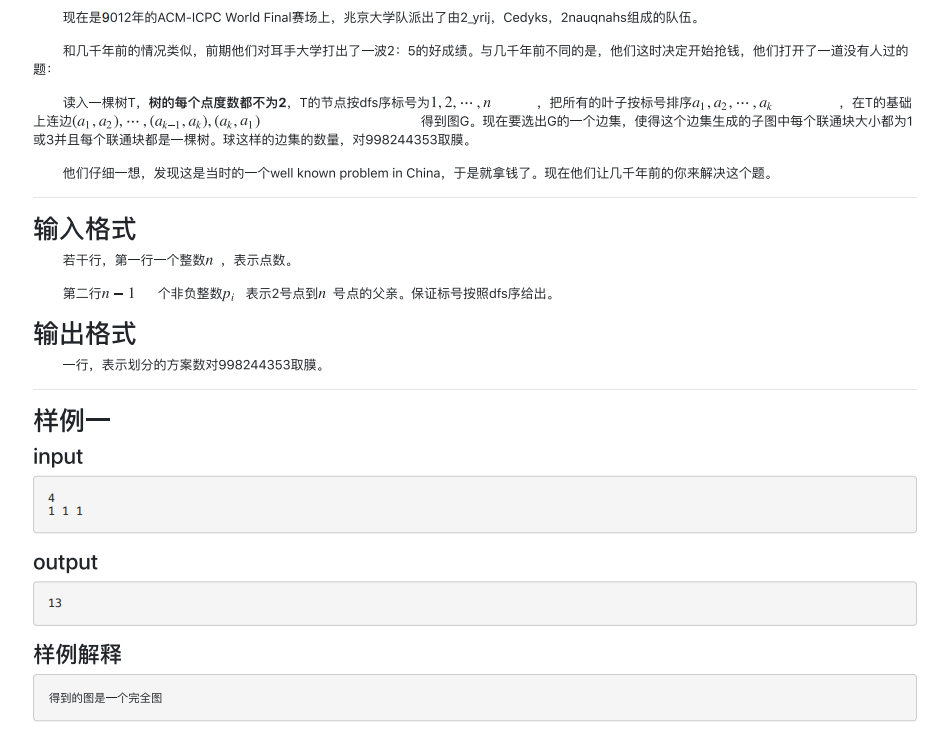
原型是树,又是计数,又不像组合,肯定是 树形dp。
考虑到“连接”情况是关注重点。考虑合并子树,既要考虑上,还要考虑下面的角角。然后最后 1 的子树还要考虑两角的连接,所以把三个角的连接情况记录了,可以发现就是下面的 3 种情况,其中第 0 种包含孤立点的情况
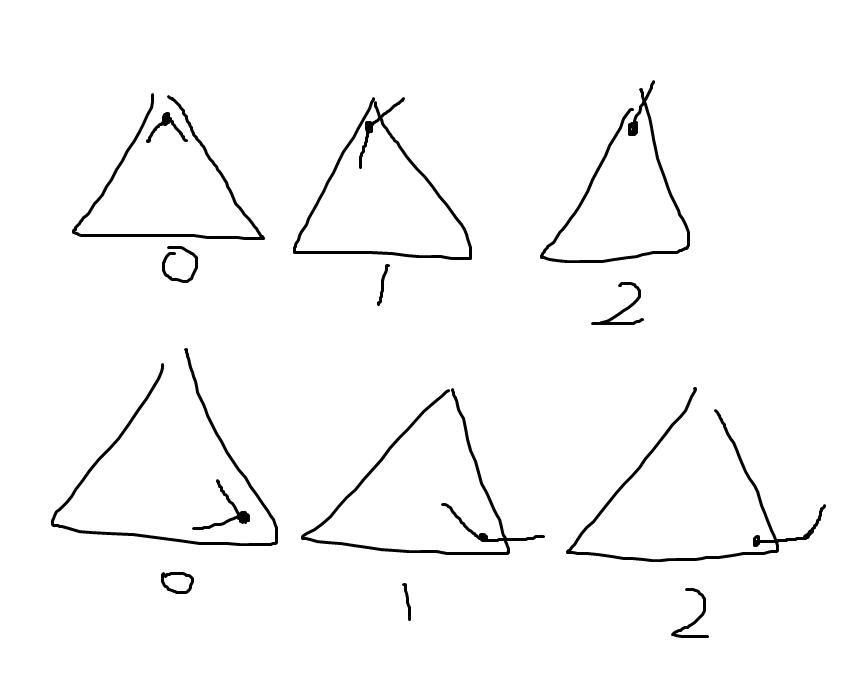
合并子树转移类似树上背包
// ubsan: undefined
// accoders
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=1e5+5,mod=998244353;
int n,f[N][3][3][3],tmp[3][3][3];
vector<int>G[N];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
void dfs(int x,int p){
f[x][0][0][0]=f[x][0][1][1]=f[x][1][1][0]=f[x][1][0][1]=f[x][2][0][0]=f[x][0][0][2]=f[x][0][2][0]=1;
int o=0;
for(int y:G[x])if(y^p){
dfs(y,x);
if(!o){
o=1;
for(int i=0;i<=2;i++)
for(int j=0;j<=2;j++)
for(int k=0;k<=2;k++)
f[x][i][j][k]=f[y][i][j][k];
}
else {
memset(tmp,0,sizeof tmp);
for(int i=0;i<=2;i++)
for(int j=0;j<=2;j++)
for(int k=0;k<=2;k++)
for(int I=0;I<=2;I++)
for(int J=0;J<=2;J++)
for(int K=0;K<=2;K++){
if(k==0&&J==0||k==1&&J==2||k==2&&J==1){
if(i==0)add(tmp[I][j][K],1ll*f[x][i][j][k]*f[y][I][J][K]%mod);
if(i==1&&I==0)add(tmp[i][j][K],1ll*f[x][i][j][k]*f[y][I][J][K]%mod);
if(i==2&&I==2)add(tmp[1][j][K],1ll*f[x][i][j][k]*f[y][I][J][K]%mod);
if(i==2&&I==0)add(tmp[i][j][K],1ll*f[x][i][j][k]*f[y][I][J][K]%mod);
}
}
for(int i=0;i<=2;i++)for(int j=0;j<=2;j++)for(int k=0;k<=2;k++)
f[x][i][j][k]=tmp[i][j][k]/*,cout<<i<<' '<<j<<' '<<k<<": "<<f[x][i][j][k]<<'\n'*/;
}
}
if(!o)return;
for(int j=0;j<=2;j++)for(int k=0;k<=2;k++){
tmp[1][j][k]=f[x][2][j][k];
tmp[2][j][k]=f[x][0][j][k];
tmp[0][j][k]=(f[x][0][j][k]+f[x][1][j][k])%mod;
}
for(int i=0;i<=2;i++)for(int j=0;j<=2;j++)for(int k=0;k<=2;k++)f[x][i][j][k]=tmp[i][j][k];
}
int main(){
freopen("graph.in","r",stdin);freopen("graph.out","w",stdout);
n=read();
for(int i=2;i<=n;i++)G[read()].emplace_back(i);
if(n==2){puts("1");return 0;}
dfs(1,0);
cout<<(1ll*f[1][0][1][2]+f[1][0][2][1]+f[1][0][0][0])%mod;
}
梦里啥都有(50pts)

我只写了50pts,在xmz的点拨下。我的dp好像有点奇怪,没有什么优化空间了,平方的。回头再说吧。
考虑到“相邻两段不能同色”的条件是主要条件,也很烦人,所以**把它容斥掉 **,具体方法是 给每个长度 L 的段定义一个新的权值 g(L),使得任意长度的同色段的所有划分的各段权值积之和恰好是 L。这样就不用管这个条件了。
一. g(L) 的求法
\(L=\sum_{1\le i<L}g(i)(L-i)+g(L)\)
解释:根据定义,L等于所有划分的权值积之和,g(L)是一种划分,剩下的划分中,我们枚举最后一段的长度 i,剩下的也是随便划分,套用定义,结合分配律,他们的和也是 L-i,便有此式。
根据他递推就好,g(0)=0
二.序列上dp
dp部分可以自己推,不说了,现在时间22:24
三.放到环上
我的做法是钦定断点处为跨断点的长度为i(枚举)的同色段,然后修改dp数组,得得得得得…………


 浙公网安备 33010602011771号
浙公网安备 33010602011771号