NOIP%2022.11
方阵
给定一个 n×n 方阵 a[i][j],和长度为 n 的数组 w[i]。
设 f[i] 为第 i 行的第 k[i] 小的区间 mex,求 max{f[i]+w[i]}。
n ≤ 10000
“第 k 小”提示了一种比较直接的做法——二分答案。对于每一行二分第 k 小的 mex,那么枚举区间右端点,左端点到它就要包含 0 ~ mid 中的所有数,可以使用并查集维护最右的左端点,统计区间个数即可。
我们发现这个做法是 \(O(n^2\log n)\) 的,无限接近 \(O(n^2)\) 的正解了,如何优化掉这个 log 呢?
我们发现其实 mex 总共就 O(n) 种,可以直接一一试探,使用上面的方法 O(n) check。具体来说,先把行按照 w 从大到小排序,维护一个 ans,每次判断 ans+1-w[i] 是否合法,合法则 ans++ 即可。
早该砍砍了
n 的排列 p 上的一次操作为选择一个区间,并把区间内所有数变成它们的 min,问任意次操作(possibly zero)能够产生多少种不同的序列。\(n\le 2000\)
我们可以设 f[i] 表示前缀 i 的方案数,f[0]=1。对于 p[i],它能够作用到的范围是前面第一个小于到后面第一个小于的开区间,推导可知 for(int j=l;j<=r;j++)f[j]+=f[j-1];,f[n] 就是答案。
棋盘染色
\(n\times m\) 的棋盘初始全为 0,每次操作可以用 w[x][y] 的代价将 (x,y) 这个位置变成 1。执行完所有操作后,如果存在一个子矩阵的三个角都是 1,那么会自动免费把第四个角染成 1,直到不存在这样的子矩阵为止。问最终棋盘全变 1 所需最小总代价。\(n,m\le 5000\)
- 关键信息是“如果存在一个子矩阵的三个角都是 1,那么可以自动免费把第四个角染成 1”,很想知道“可以通过第二个操作把棋盘全部变成 1”这句话背后到底藏着什么
- 以点为对象的二维染色问题,不难使用经典套路——行列二分图
把两者有机结合一下,可以发现充要条件是图联通!于是变成了最小生成树问题,可用桶排代替 sort 做到 \(O(n^2)\)。
数三角
一个边被黑白染色的完全图中有多少个同色三角形?\(n\le 8000\)
正难则反,统计异色三角形个数。必然是一种颜色有一次、另一种颜色两次,我们如果能在黑白边交点处统计到这个三角形,只需要把答案除以 2 就可以输出了。
二择
有一个点数是 3×n,边数是 m 的无向图。称一个点集是 1 的,当且仅当其间没有连边;称一个边集是 2 的,当且仅当没有两条边有公共顶点。你需要找到一个大小为 n 的 1 的点集或一个大小为 n 的 2 的边集,或输出无解。\(n,m\le 2\times 10^5\)
3×n 看起来很蹊跷;我们需要一个切入点,也就是翻译一下题意。1 不好翻译,2 就是一个【匹配】,当我们在图中描绘出一个最大匹配时,就会知道剩下的点都是满足“其间没有连边”的。原来 n 条边的 2 边集是包含 2n 个点的,如果不足 n 条边则剩下的点集是至少 n 个点的。
数塔
\(n\le 5\times 10^5\)
赛时许多人通过只进行 10 层递推操作,成功水过此题,数据太水强烈谴责
其实看到中位数我是敏感地想到了二分答案变成 01 之类的东西,但是不知道进一步该怎么做,感觉跟没转化前无别。
事实上就差一步了:通过手推几组数据找规律可以发现,最终最上面的数恰恰就是离中线最近的同色相邻对的颜色。特判一下不存在同色相邻对的情况(一直是黑白相间)
Camel and Oases
重复
一个字符串的一种剖分为将它分割成 6 个非空段,依次叫做 \(a,b,c,d,e,f\),当它们形如 114514(即 \(a=b=e,c=f\))时是一种合法剖分。求仅包含 0 ~ 9 的字符串 \(S\) 的所有子串的合法剖分数之和。\(|S|\le 5000\)
又是一道 114514 题。它跟上一道 114514 题没有什么相似性,而且那个题是关于子序列,这题 abcdef 要一个连一个,所以那题的思路没什么可借鉴的。
观察 114514,这个 14514 比较的有趣,因为 14 和 14 是一样的,这个不是回文对吧,想想看这个叫什么来着,哦对,border。诶那不是 KMP 吗?KMP 可不可以做啊?好像可以,固定左端点,往右枚举串的右端点,就能知道每一个 border 的信息;预处理出左端点作为中介的 11 有多少个(\(O(n^2)\)),做个前缀和,就可以每次 O(1) 查询增量,做完了。
公交
一个 \(n\) 个点的数,当它以 \(r\) 为根时,你需要选择 \(k\) 条以 \(r\) 为一端的路径,包含于至少一条路径上的点被称为可用的点,每个点到距离它最近的可用点的距离乘以它的点权为它的代价,要求最小化所有点的总代价。对于 \(r=1,2,...,n\) 都输出答案。\(n\le 10^5\)
考虑一条路径带来的影响。如果乍看看不出来的话,考虑以一定的顺序观察,这样往往能够发现变化量的规律。换句话说就是从根开始依次加入路径上的点,对答案的影响是什么?依次加入到当前点,恩泽所及之点便是它的子树之中的点,根据定义,答案的减少量应该就是子树中的权值和。因此一条路径的代价为路径上所有点的子树中点权和之和(重复经过的点不算)。这个就跟 accoders 上一道题比较像,是个长链剖分贪心可以解决的问题,这里略过。
考虑如何换根。换根就是要看换根前后哪些点的信息受到了影响,影响了多少。经过仔细分析不难发现受到影响的应该最多有 2 个点,因此可以暴力地维护一个 set 来表示每条长链的价值(这样可能稍有别扭,可以考虑开两个 set,一个维护前 k 大,一个存其余)。
乘筛积
给定 \(n,m,C,a_{1..n},b_{1..m}\),\(T\) 次询问 \(p,q\),要求回答 \(\sum_{px+qy=C,x\in[1,n],y\in [1,m]}a_xb_y\)。
\(n,m,C,p,q,T\le 3\times 10^5,1\le a_i,b_i<2^{31}\)
题解做法:根号分治。
首先 exgcd 求出一组特解和两者的公差,然后暴力模拟统计答案。这是一个暴力的思路,我们考虑使用根号分治优化。
对 \(\max(p,q)\) 根号分治,如果小于根号,由于公差分别小于 \(p,q\),这部分总复杂度为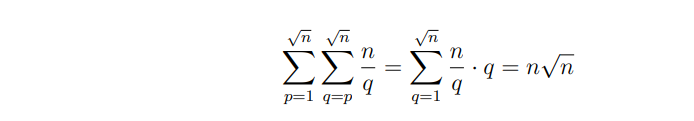
而如果大于根号,虽然公差不一定大于根号,但也都接近于大于根号,感性理解 不会增加复杂度,所以总复杂度其实是 \(n\sqrt n\) 的,前面的部分可以通过对 p,q 记忆化完成。
放进去
给 \(n\) 个位置染色,共有 \(m\) 种可供选择的颜色。如果第 \(i\) 种颜色被使用过,那么需要支付 \(b_i\) 的代价;如果第 \(i\) 个位置染成了第 \(j\) 种颜色,需要支付 \(a_{i,j}\) 的代价。最小化总代价。\(n\le 10^5,m\le 25,1\le a,b\le 10^9\)
首先这个 \(m\) 为什么是 \(25\) 会吸引我们的眼球,细想会发现是个状压提示,这样一来,一个直观的认识是如果我们选择了子集 \(S\) 内的颜色,那么第二方面的总代价应该是对于所有位置,选择 \(S\) 内的该位置的 \(a\) 最小的那个。但是我们同样可以直观地发现要把 \(n\) 个最小值相加是一件难以快速实现的事情——由于这个“各位置对应min”的限制,我们不得不去枚举每个位置,从而导致复杂度超标;而如果能够把 min 也变成 ∑ 的形式,就会非常好。
【Trick】选择若干个元素 所选元素的权值中最小的那个是多少,这个问题可以转化为:对于每一个完整包含所选元素集的后缀(按照权值从小到大排序之后),有一个 \(a_p-a_{p-1}\) 的权值,那么由于包含它的后缀的左端点是一个前缀,我们用高维前缀和做一个超集前缀和就可以了。
对于这题而言,最后还需要对于每个 mask 把所得的超集权值和加上所选颜色的 ∑b,由于此题卡常,就用 \(O(2^m)\) 的递推求这才能过。
最长路径
先吐槽一下其卡常和码农。
我觉得题解写得很好,你可以把它换一下

评一下,【套路】并查集可以用来线性(忽略 \(\alpha\))解决多次的区间覆盖问题,原理是离线并按照覆盖优先级排序(例如,越靠后的覆盖越优先、本题中就是 \(c_2\) 越大的越优先,等),那么优先覆盖的位置从今往后都不更改了,删掉这个位置,可以看成若干个连续段,没个连续段有且只有右端点处是没删掉的,通过并查集维护 find(i) 表示 i 所在的块的右端点,改完就删即可。
//火车头就略了
#include <bits/stdc++.h>
#define rsz(d) d[i].resize(m+1)
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x/10)print(x/10);
putchar(x%10+48);
}
const int N=2005,kQ=5e5+5,mod=1e9+7;
int n,m,q,Q0[N],ql1[N],qr1[N],buc0[N],d[N][N],r[N][N],f[N][N],g[N][N],g0[N][N],g1[N][N],fa[2][N][N],Q1[N][N],buc1[N][N];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline void sub(int &x,int y){(x-=y)<0&&(x+=mod);}
struct Rect{int r1,c1,r2,c2;}rc[kQ];
int find(int ty,int id,int x){return x==fa[ty][id][x]?x:fa[ty][id][x]=find(ty,id,fa[ty][id][x]);}
void solve(){
n=read(),m=read(),q=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)d[i][j]=r[i][j]=f[i][j]=0,g[i][j]=g1[i][j]=g0[i][j]=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m+1;j++)fa[0][i][j]=j;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n+1;j++)fa[1][i][j]=j;
for(int j=0;j<=min(n,m);j++)buc1[i][j]=0;
}
for(int o=1;o<=q;o++)rc[o].r1=read(),rc[o].c1=read(),rc[o].r2=read(),rc[o].c2=read();
sort(rc+1,rc+q+1,[](Rect a,Rect b){return a.c2>b.c2;});
for(int i=1;i<=q;i++){
if(rc[i].r1==rc[i].r2)continue;
for(int j=find(1,rc[i].c1,rc[i].r1);j<rc[i].r2;j=find(1,rc[i].c1,j+1))
r[j][rc[i].c1]=rc[i].c2,fa[1][rc[i].c1][j]=j+1;
}
sort(rc+1,rc+q+1,[](Rect a,Rect b){return a.r2>b.r2;});
for(int i=1;i<=q;i++){
if(rc[i].c1==rc[i].c2)continue;
for(int j=find(0,rc[i].r1,rc[i].c1);j<rc[i].c2;j=find(0,rc[i].r1,j+1))
d[rc[i].r1][j]=rc[i].r2,fa[0][rc[i].r1][j]=j+1;
}
for(int i=1;i<=n;i++)for(int j=2;j<=m;j++)r[i][j]=max(r[i][j],r[i][j-1]);
for(int i=1;i<=m;i++)for(int j=2;j<=n;j++)d[j][i]=max(d[j][i],d[j-1][i]);
int ans=-1,ans2=0;
for(int i=1;i<=m;i++)ql1[i]=1,qr1[i]=0;
for(int i=n;i;i--){
if(i<n){
int ql0=1,qr0=0;
for(int j=0;j<=min(n,m);j++)buc0[j]=0;
for(int j=m;j;j--){
while(ql0<=qr0&&Q0[ql0]>r[i][j])sub(buc0[f[i+1][Q0[ql0]]],g0[i+1][Q0[ql0]]),ql0++;
if(j+2<=m&&j+2<=r[i][j]){
while(ql0<=qr0&&f[i+1][j+2]>f[i+1][Q0[qr0]]){
sub(buc0[f[i+1][Q0[qr0]]],g0[i+1][Q0[qr0]]);
qr0--;
}
Q0[++qr0]=j+2,add(buc0[f[i+1][j+2]],g0[i+1][j+2]);
}
if(ql0<=qr0){
int sumg=buc0[f[i+1][Q0[ql0]]];
if(f[i][j]<f[i+1][Q0[ql0]]+1)f[i][j]=f[i+1][Q0[ql0]]+1,g[i][j]=sumg;
else if(f[i][j]==f[i+1][Q0[ql0]]+1)add(g[i][j],sumg);
}
}
}
for(int j=1;j<=m;j++){
if(j<m){
while(ql1[j+1]<=qr1[j+1]&&Q1[j+1][ql1[j+1]]>d[i][j])sub(buc1[j+1][f[Q1[j+1][ql1[j+1]]][j+1]],g1[Q1[j+1][ql1[j+1]]][j+1]),ql1[j+1]++;
if(ql1[j+1]<=qr1[j+1]){
int sumg=buc1[j+1][f[Q1[j+1][ql1[j+1]]][j+1]];
if(f[i][j]<f[Q1[j+1][ql1[j+1]]][j+1]+1)f[i][j]=f[Q1[j+1][ql1[j+1]]][j+1]+1,g[i][j]=sumg;
else if(f[i][j]==f[Q1[j+1][ql1[j+1]]][j+1]+1)add(g[i][j],sumg);
}
}
if(ans<f[i][j])ans=f[i][j],ans2=g[i][j];
else if(ans==f[i][j])add(ans2,g[i][j]);
g0[i][j]=g1[i][j]=g[i][j];
while(ql1[j]<=qr1[j]&&f[Q1[j][qr1[j]]][j]<f[i][j]){sub(buc1[j][f[Q1[j][qr1[j]]][j]],g[Q1[j][qr1[j]]][j]);
qr1[j]--;
}
Q1[j][++qr1[j]]=i,add(buc1[j][f[i][j]],g1[i][j]);
}
}
print(ans+1),putchar(' '),print(ans2),putchar('\n');
}
int main(){
freopen("path.in","r",stdin);freopen("path.out","w",stdout);
int T=read();
while(T--)solve();
}
排序
Inversion Swapsort
冒泡排序交换相邻,本题交换逆序对,所以想办法让下标的逆序体现在值域上,这样就没有限制了,手推可发现,排列的逆上做冒泡排序是可达到目的的。
Xorum
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct node {int t,x,y;}; vector<node>vec;
inline void st(int t,int x,int y){vec.push_back(node{t,x,y});}
int work(int x){
int bit=0;
for(int i=20;~i;i--)if(x>>i&1){bit=i;break;}
int y=x;
while(bit--)st(1,y,y),y<<=1;
st(2,x,y);
int z=x^y;
st(1,y,z);
int p=z+y;
st(2,x,p);
int q=x^p;
st(1,y,y);
int o=y+y;
st(2,o,q);
int h=o^q,tmp=h>>1;
int yy=y-tmp;
while(yy){
if((yy&-yy)==h)st(2,h,y),yy-=h,y-=h;
st(1,h,h),h<<=1;
}
st(2,tmp,x);
return tmp^x;
}
signed main(){
int x;
cin>>x;
while(x>1)x=work(x);
cout<<vec.size()<<'\n';for(auto p:vec)if(p.t==1)printf("%lld + %lld\n",p.x,p.y);
else printf("%lld ^ %lld\n",p.x,p.y);
}
Intresting Sections
https://www.luogu.com.cn/problem/CF1609F
【Trick】数区间问题,只有两种方法:(1)分治(2)固定左端点扫右端点
本题中我们采用前者。现在求出 \([L,R]\) 跨 \(mid\) 的答案。
从 \(mid\) 到 \(L\) 枚举区间的左端点 \(l\),右端点 \(r\) 的三种不同取值范围对应了三种不同统计方法
- \(r\in [mid+1,p_1]:\min_{[mid+1,r]}\ge\min_{[l,mid]}且\max_{[mid+1,r]}\le\max_{[l,mid]}\):一个满足要求的区间的 max 和 min 都在左半部分取到,只需预处理左半部分的每个后缀的 max 和 min 的 popcount 相等与否。
- \(r\in (p_1,p_2]:\min_{[mid+1,r]}< \min_{[l,mid]}和\max_{[mid+1,r]}>\max_{[l,mid]}中恰有其一满足\):一个满足要求的区间的 max 和 min 二选一在左半部分取到,另一个在右半部分取到,由于此时已经知道 \(\min/\max_{[l,mid]}\),所以右边的 \(\min/\max\) 的 popcount 也知道了,只需查询一个区间内前缀 min/max 的 popcount 为某一定值的点有几个,使用桶+差分做。
- \(r\in (p2,n]:\min_{[mid+1,r]}< \min_{[l,mid]}且\max_{[mid+1,r]}>\max_{[l,mid]}\):一个满足要求的区间的 max 和 min 都在右半部分取到,只需预处理出一个区间内前缀 min/max 相等的点的个数即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=1e6+5,INF=2e18;
int n,ans,a[N],c3[N],mn2[N],mx2[N],bucmn[64],bucmx[64],arr[N],ppc[N];
map<int,int>mp;
inline int Popc(int x){int cnt=0;while(x)cnt++,x-=x&-x;return cnt;}
#define popc(x) ppc[x]
void solve(int l,int r){
if(l==r){
ans++;
return;
}
int mid=l+r>>1,p1=mid,p2=mid;
mx2[mid]=-INF,mn2[mid]=INF;
c3[mid]=0;
for(int i=mid+1;i<=r;i++){
mn2[i]=min(mn2[i-1],a[i]),mx2[i]=max(mx2[i-1],a[i]);
c3[i]=c3[i-1]+(popc(mx2[i])==popc(mn2[i]));
}
int mx=-INF,mn=INF;
for(int i=mid;i>=l;i--){
mn=min(mn,a[i]),mx=max(mx,a[i]);
while(p2<r&&(mn<=mn2[p2+1]||mx>=mx2[p2+1]))p2++,bucmn[popc(mn2[p2])]++,bucmx[popc(mx2[p2])]++;
while(p1<p2&&mn<=mn2[p1+1]&&mx>=mx2[p1+1])p1++,bucmn[popc(mn2[p1])]--,bucmx[popc(mx2[p1])]--;
if(popc(mn)==popc(mx))ans+=p1-mid;
if(mn>mn2[p2])ans+=bucmn[popc(mx)];
else ans+=bucmx[popc(mn)];
ans+=c3[r]-c3[p2];
}
while(p2>p1)bucmn[popc(mn2[p2])]--,bucmx[popc(mx2[p2])]--,p2--;
solve(l,mid),solve(mid+1,r);
}
signed main(){
//freopen("interval.in","r",stdin);freopen("interval.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)a[i]=read(),arr[i]=a[i];
sort(arr+1,arr+n+1);
int u=unique(arr+1,arr+n+1)-arr-1;
for(int i=1;i<=u;i++)mp[arr[i]]=i;
for(int i=1;i<=n;i++)a[i]=mp[a[i]];
for(int i=1;i<=u;i++)ppc[i]=Popc(arr[i]);
solve(1,n);
cout<<ans<<'\n';
}
Cleaning
https://www.luogu.com.cn/problem/AT_agc010_c
前置知识:套路题条件反射第 39 条(CF 上叫 Zero Sum)
首先还原出那个树上差分的数组 \(c\),自下而上处理每个非叶子节点,这样遇上的时候它上面写着一个负数,它的绝对值就代表子树有多少条跨越它的路径,然后由于树上差分的过程,我们要把 \(c[fa[u]]-=c[u]\),到时才能得到真正的 \(c[fa[u]]\)。现在对于 \(u\),它的每个儿子子树都会有一些过剩的叶子上的值,这里就变成了“前置知识”中的问题,求最后最少剩几个(我们一定希望剩得越少越好,因为如果少的不行,多的也肯定不行)。最终看一下剩不剩就行了。注意在途中判断 c 是否为负值。
机器战警
\(n,m\le 10^7\)
由于机器人的行走实质上是坐标的变化,我们可以令 L = -1, R = 1。对于一个操作子串 [l,r],若存在一个前缀和 S(l,p)>n-x,在 x 处出发执行 [l,r] 操作序列必然爆炸;否则,如果其最大子段和 ≥ n,也必然爆炸;否则不爆炸。
于是,对于每一个最大子段和 ≤ n - 1 的子串 [l,r],x_max = n - 最大前缀和。
这可以通过倒序枚举左端点并控制右端点的指针,并维护 [l,r] 内前缀和的单调队列来办到。具体见代码。
#include <bits/stdc++.h>
using namespace std;
inline char readc(){
register char ch=getchar();
while(ch!='L'&&ch!='R')ch=getchar();
return ch;
}
const int N=1e7+5,mod=1e9+7;
int n,m,ql,qr,tp,a[N],pre[N],Q[N],stk[N],suc[N];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++)a[i]=(readc()=='L'?-1:1);
for(int i=1;i<=m;i++)pre[i]=pre[i-1]+a[i];
for(int i=m;i;i--){
while(tp&&pre[stk[tp]]<=pre[i])tp--;
if(tp)suc[i]=stk[tp];else suc[i]=m+1;
stk[++tp]=i;
}
ql=m+1,qr=m;
int ans=0,cnt=0,sum=0;
for(int i=m,j=m;i;i--){
while(ql<=qr&&pre[Q[ql]]<pre[i])ql++;
Q[--ql]=i;
while(j>=i&&(ql<=qr&&pre[Q[qr]]-pre[i-1]>n-1)){
sum-=pre[Q[qr]],sum%=mod,(sum+=mod)%=mod;
if(ql<=qr&&Q[qr]==j)qr--;
j--;
}
if(i<=j)sum+=pre[i],sum%=mod,(sum+=mod)%=mod;
(cnt+=(j-i+1ll)*((n+pre[i-1]+mod)%mod)%mod)%=mod;
for(int k=i+1;k<=min(j,suc[i]-1);k=suc[k])add(sum,1ll*(pre[i]-pre[k]+mod)*(min(min(j,suc[k]-1),suc[i]-1)-k+1)%mod);
//(2+2)+(2+1)+(2+2)*2+(2+1)*3+(2)=4+3+8+9+2=26
add(ans,(sum+(max(0ll,(long long)pre[i-1]-pre[i])+mod)%mod*(min(suc[i]-1,j)-i+1))%mod);
}
cout<<(cnt-ans+mod)%mod;
}
子串划分
对 \(S\) 的 \(2^{n-1}\) 种划分,将每一段插入字典树,求字典树的大小之和。\(|S|\le 2000\)
划分字典树含于后缀字典树,先建出后缀字典树,考虑每个节点的贡献(1×在几种方案中存在过)。
每个节点对应一条从根到它的路径所代表的子串,这些子串是互异的(所以其实没必要显式建树,但是这样还是方便些)。我们找到这个子串在原串中的每一次出现的起始位置 \(st_1,...,st_{num}\);它对一个方案有贡献当且仅当这个方案中有至少一个段从某个 \(st\) 开始,并完整地包含了它。“至少一个”启发我们容斥,但由于重重叠叠的位置关系的复杂性,我们考虑用 dp 的角度考虑,设 \(f_i\) 表示阶段到了 \(st_i\) 这个串,不存在任何一个段算过的方案数,\(f_0=2^{n-1}\)。那么 \(f_{i}\) 就需要用 \(f_{i-1}\) 减去 \(st_i\) 这个串被包含且前面都没被包含过的方案数。后者就是 \(\frac{f_j}{2^{len}}\),\(j\) 表示往前数第一个不跟 \(st_i\) 重叠的 \(st\) 串。原因在于重叠的肯定已经没被包含过(因为我们在 \(st_i\) 前面放了一个挡板)。特别注意当 \(st_i=1\) 时,只用 \(\frac{f_j}{2^{len-1}}\),因为前面的挡板不用钦定,永远在那儿。
关于时间复杂度:我们应该用 \(O(occ(str))\) 的时间处理 \(str\) 的贡献,这样总复杂度就是所有互异子串的出现次数之和,等于总子串个数 \(O(n^2)\)。可以通过预处理来办到。
UER#11 切割冰片
经过少量的 observe 可以将问题转化为:初始时有一个集合 \(\{1,2,...,n,+\infin\}\),在 \(l_1+1,l_2+1,...\) 这 \(n\) 个时刻分别删除 \(1,2,...\) 这些数,要求在时刻 \(1\sim m\) 的集合中分别选一个数,使得形成的序列随着时间轴而不降,求方案数。
显然的 dp,转移就是做前缀和,删除 \(i\) 时就把对应的 \(f_i\) 删掉。这样就是 \(O(nm)\) 的,如果卡常的话可以获得 80 分,但是我不知道 5e8 是可以 1s 过的,所以没有卡常,只有 60 分。
每次转移就是对 dp 数组做前缀和的 dp 可以通过路径计数优化。对 \(f_i\) 进行 \(k\) 次前缀和运算,得到的 \(f_i'\),可 \(O(n^2)\) 枚举 \(i,j(i\le j)\),并计算 \(f_i\) 对 \(f_j'\) 的贡献 \(f_j'+={j-i+k-1\choose j-i}f_i\)。而总共只会进行 \(O(n)\) 次删除,也就是 \(O(n)\) 次进行这种 \(O(n^2)\) 的批量前缀和转移。
#include <bits/stdc++.h>
using namespace std;
const int N=505,mod=998244353;
int m,n,l[N],ord[N],tmp[N],C[N],bk[N],jc[N],inv[N];
vector<int>f;
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline int qp(int a,int b){
int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;return c;
}
inline void Erase(int id){
for(vector<int>::iterator it=f.begin();it!=f.end();it++){
if(!id){f.erase(it);break;}
id--;
}
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)scanf("%d",&l[i]),l[i]++,ord[i]=i;
for(int i=1;i<=n+1;i++)inv[i]=qp(i,mod-2);
sort(ord+1,ord+n+1,[&](int i,int j){return l[i]<l[j];});
f.resize(n+2);
for(int i=1;i<=n+1;i++)f[i]=1;
l[0]=1;
int las=1;
for(int i=1;i<=n;i++){
if(l[ord[i]]>m)break;
for(int j=1;j<f.size();j++)tmp[j]=0;
C[0]=1;
for(int d=1;d<=n+1;d++){
C[d]=1ll*C[d-1]*(l[ord[i]]-l[ord[i-1]]-1+d)%mod*inv[d]%mod;
}
if(l[ord[i]]!=l[ord[i-1]]){
for(int j=1;j<f.size();j++)for(int k=j;k<f.size();k++){
add(tmp[k],1ll*f[j]*C[k-j]%mod);
}
}
else {
for(int j=1;j<f.size();j++)tmp[j]=f[j];
}
for(int j=1;j<f.size();j++)f[j]=tmp[j];
bk[ord[i]]=1;
int num=0;
for(int j=1;j<=ord[i];j++)num+=bk[j];
Erase(ord[i]-num+1);
las=l[ord[i]];
}
for(int j=1;j<=n+1;j++)tmp[j]=0;
C[0]=1;
for(int d=1;d<=n+1;d++){
C[d]=1ll*C[d-1]*(m-las-1+d)%mod*inv[d]%mod;
}
if(m!=las){
for(int j=1;j<f.size();j++)for(int k=j;k<f.size();k++){
add(tmp[k],1ll*f[j]*C[k-j]%mod);
}
}
else {
for(int j=1;j<f.size();j++)tmp[j]=f[j];
}
for(int j=1;j<f.size();j++)f[j]=tmp[j];
int ans=0;
for(int i=1;i<f.size();i++)add(ans,f[i]);
cout<<ans;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号