Trick: 树上点边容斥
核心观点:\(\bm n\) 个点的树上点亮的灯构成的连通块个数 = 点亮的点数 - 两端都点亮的边数。
关键词:灯,连通块,点亮的点数,两端都点亮的边数。
用途:将不方便统计的“连通块个数”转化为易于统计的“点亮的点数”和有办法统计的“两端都点亮的边数”。
【例1】(广铁一中模拟赛·2022.10)灯

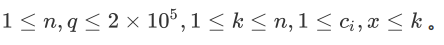
显然是一道 DS 题。想了一会可以发现没有什么数据结构能维护这种东西,故考虑暴力算法(分块等)。分块好像也不行,另一种分块——根号分治貌似很可行,因为每个点只属于一个开关,所以对于小开关暴力,大开关怎么弄一下按说能做出来。
然后由于我们要统计亮灯的连通块数,联想到树上点边容斥(链是特殊的树),所求即为 点亮的点数 - 相邻两个都点亮的对数。前者极易统计,考虑后者。
对于所控制的灯数小于根号的开关的状态反转,我们可以就维护一个序列 \(lit\) 代表每个位置是否点亮,然后每次枚举这个开关的灯看一下左右相邻位置是否点亮然后直接统计。当然,对于所有的开关,我们都要预处理出只打开它时的相邻点亮对数。
对于所控制的灯数大于根号的开关,我们可以发现跟它中灯相邻的灯要么是大开关的灯要么是小开关的灯。如果是大开关的灯,由于大开关总共就根号个,所以存一下是哪些,到时暴力判断每一个是否点亮然后计数器加上 只打开他俩开关时的相邻点亮对数 即可,后者需要预处理。如果是小开关的灯,我们考虑在小开关进行遍历的时候就把这个大开关上打上标记,代表改变大开关的状态会带来的影响,这样便可以在大开关的状态切换时直接加上这个变化量(具体的实现细节不难自己摸索)。
至此我们在 \(O(q\sqrt n)\) 的时间内解决了这个问题。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x<0){putchar('-'),print(-x);return;}
if(x/10)print(x/10);
putchar(x%10+48);
}
const int N=2e5+5;
int n,q,K,tot,B,bel[N],r[500][500],cnt[N],tag[N],ibig[N];
bool bk[N],lit[N];
vector<int>own[N],big,adj[N];
set<int>tmp;
int main(){
n=read(),q=read(),K=read(),B=sqrt(n);
for(int i=1;i<=n;i++)bel[i]=read(),own[bel[i]].push_back(i);
for(int i=1;i<=K;i++){
if(own[i].size()>B)ibig[i]=big.size(),big.push_back(i);
for(int j=1;j<own[i].size();j++)
if(own[i][j]==own[i][j-1]+1)cnt[i]++;
}
int i_1=0,i_2=0,all=0;
for(int i:big){
for(int j:own[i])bk[j]=1;
i_2=0;
for(int j:big){
if(i^j)for(int k:own[j])r[i_1][i_2]+=bk[k-1]+bk[k+1];
i_2++;
}
for(int j:own[i])bk[j]=0;
i_1++;
tmp.clear();
for(int j:own[i]){
if(j>1)tmp.insert(bel[j-1]);
if(j<n)tmp.insert(bel[j+1]);
}
for(int j:tmp)if(own[j].size()>B&&i!=j)adj[i].emplace_back(j);
}
int ans=0;
for(int x;q--;){
x=read(),lit[x]=!lit[x];
int F=1;
if(!lit[x])F=-1;
if(own[x].size()<=B){
for(int i:own[x]){
if(i>1&&bel[i-1]!=x){
if(own[bel[i-1]].size()<=B)ans+=F*lit[bel[i-1]];
else {
if(lit[bel[i-1]])ans+=F,tag[bel[i-1]]-=F;
else tag[bel[i-1]]+=F;
}
}
if(i<n&&bel[i+1]!=x){
if(own[bel[i+1]].size()<=B)ans+=F*lit[bel[i+1]];
else {
if(lit[bel[i+1]])ans+=F,tag[bel[i+1]]-=F;
else tag[bel[i+1]]+=F;
}
}
}
}
else {
ans+=tag[x],tag[x]=-tag[x];
for(int i:adj[x])if(lit[i])ans+=F*r[ibig[x]][ibig[i]];
}
all+=F*own[x].size(),ans+=F*cnt[x];
print(all-ans),putchar('\n');
}
}
【例2】[北大集训2021]小明的树
一棵树是美丽的当且仅当:连通块个数 = 两头异色的边数
代入“连通块个数 = 点亮的点数 - 两头点亮的边数”,得:点亮的点数 = 至少一头点亮的边数
容易想到维护加边的过程中等式右侧的值 \(val_{右}\),这是一个长 \(n-1\) 的序列。查询的就是所有 \(val_{右i}-i=0\) 的位置的权值和。一个位置的权值为那时的连通块个数,即两头异色的边数。
显然,一条边 \((u,v)\) 给答案产生的贡献就是给 \(val_{右}\) 的一个后缀 \(±1\),这个后缀的起点是 \(\min(t_u,t_v)\)(当统计的是至少一头点亮的边数时)。对于权值序列的修改,显然就是 \([\min(t_u,t_v),\max(t_u,t_v))\) 的区间 \(±1\)。以上 \(t_u\) 表示的是 \(u\) 在点灯排列中的时间戳(\(\in [1,n-1]\))。
考察 \(val_{右i}-i\),由于每个被点亮的点的父边都属于“至少一头点亮的边”,因此 \(val_{右i}-i\) 恒 \(\ge 0\),因而,我们只需要维护 \(val_{右i}-i\) 的最小值(就是把初值设成 \(-i\))、最小值的个数、最小值对应位置的权值和,即可。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=5e5+5;
int n,q,u[N],v[N],tim[N],mn[N<<2],cnt[N<<2],tag[N<<2],tag2[N<<2];
long long sum[N<<2];
void pushup(int k){
if(mn[k<<1]<mn[k<<1|1])mn[k]=mn[k<<1],cnt[k]=cnt[k<<1],sum[k]=sum[k<<1];
else if(mn[k<<1]>mn[k<<1|1])mn[k]=mn[k<<1|1],cnt[k]=cnt[k<<1|1],sum[k]=sum[k<<1|1];
else mn[k]=mn[k<<1],cnt[k]=cnt[k<<1]+cnt[k<<1|1],sum[k]=sum[k<<1]+sum[k<<1|1];
}
void pushdown(int k){
if(tag[k]){
tag[k<<1]+=tag[k],tag[k<<1|1]+=tag[k];
mn[k<<1]+=tag[k],mn[k<<1|1]+=tag[k];
tag[k]=0;
}
if(tag2[k]){
tag2[k<<1]+=tag2[k],tag2[k<<1|1]+=tag2[k];
sum[k<<1]+=1ll*tag2[k]*cnt[k<<1];
sum[k<<1|1]+=1ll*tag2[k]*cnt[k<<1|1];
tag2[k]=0;
}
}
void build(int l,int r,int k){
if(l==r){mn[k]=-l,cnt[k]=1,sum[k]=0;return;}
int mid=l+r>>1;
build(l,mid,k<<1),build(mid+1,r,k<<1|1);
pushup(k);
}
void chg(int L,int R,int v,int l,int r,int k){
if(L<=l&&r<=R){mn[k]+=v;tag[k]+=v;return;}
pushdown(k);
int mid=l+r>>1;
if(L<=mid)chg(L,R,v,l,mid,k<<1);
if(R>mid)chg(L,R,v,mid+1,r,k<<1|1);
pushup(k);
}
void chg2(int L,int R,int v,int l,int r,int k){
if(L<=l&&r<=R){tag2[k]+=v,sum[k]+=1ll*cnt[k]*v;return;}
pushdown(k);
int mid=l+r>>1;
if(L<=mid)chg2(L,R,v,l,mid,k<<1);
if(R>mid)chg2(L,R,v,mid+1,r,k<<1|1);
pushup(k);
}
int ask(){
if(mn[1])return 0;
return sum[1];
}
int main(){
n=read(),q=read();
for(int i=1;i<n;i++)u[i]=read(),v[i]=read();
for(int i=1;i<n;i++)tim[read()]=i;
build(1,n-1,1);
tim[1]=1e9;
for(int i=1;i<n;i++){
if(tim[u[i]]>tim[v[i]])swap(u[i],v[i]);
chg(tim[u[i]],n-1,1,1,n-1,1);
chg2(tim[u[i]],tim[v[i]]-1,1,1,n-1,1);
}
cout<<ask()<<'\n';
for(int u1,v1,u2,v2;q--;){
u1=read(),v1=read(),u2=read(),v2=read();
if(tim[u1]>tim[v1])swap(u1,v1);
if(tim[u2]>tim[v2])swap(u2,v2);
chg(tim[u1],n-1,-1,1,n-1,1);
chg2(tim[u1],tim[v1]-1,-1,1,n-1,1);
chg(tim[u2],n-1,1,1,n-1,1);
chg2(tim[u2],tim[v2]-1,1,1,n-1,1);
cout<<ask()<<'\n';
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号