NOIP%10.8~10.31
药丸(原题)
一个长为 \(n\) 的空序列,每个位置可以随便填
0/(/)之一,如果去除 0 后不存在失配的),并且失配(的个数 \(\in[l,r]\),则称其为一合法括号序列。问有多少种填法使得得到的序列合法。\(0\le l\le r\le n\le 10^5\),模数 \(p\le 2\times 10^9\) 不保证是质数。
很显然的 dp 是设 f[i][j] 表示前缀 i 失配 j 个 ( 的方案数,有:(1)f[i][j]=f[i-1]j+1(2)f[i][j]=f[i-1][j-1]+f[i-1]j+1。根据常见套路,可以视作平面走动,方向是向右上或向右下,从 (0,0) 走到 (n,i) 的方案数就是 f[n][i],那么就是 \(n\choose {n-i\over 2}\)。但是——我们发现不对劲!因为可能走到 x 轴以下,而这是被严禁的。我当时本来按照错误的思路写到了 \(\sum_{i=0}^n{n\choose i}\sum_{j=\lceil (i-r)/2\rceil}^{\lfloor (i-l)/2\rfloor}{i\choose j}\),然后思路就被打断了,没有想到什么好的解决办法,发现时间不太够就去打暴力了。然而,这个思路其实已经非常接近正解了。
我们考虑多算了甚麽,明显是“触碰到”y=-1 的走法们。于是我们减掉即可。如何钦定一个走法必须触碰 y=-1,根据将军饮马原理不难得出是 (0,-2) 走到 (n,i) 的方案数(走法还是没有限制的右上和右下),即 \(n\choose {n-i-2\over 2}\)原因在于我们欲达到目标必须越过该直线。只需要在上面的式子上减去一下就好了:
可以看到这个式子通常可以直接求了,只要会算组合数模 p 就可以了,但是 p 不是质数的情况怎么算呢?
不会的同学可以看 套路题条件反射 No.26 条。
代码:
#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define int unsigned
using namespace std;
const int N=1e5+5;
int n,mod,l,r,tot,jc[N],ijc[N],pr[15],ci[15][N];
inline int qp(int a,int b){
int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
return c;
}
void init(){
int pp=mod,phi=mod;
for(int i=2;i*i<=pp;i++)if(pp%i==0){
pr[++tot]=i;
while(pp%i==0)pp/=i;
phi-=phi/i;
}
if(pp>1)phi-=phi/pp,pr[++tot]=pp;
jc[0]=ijc[0]=1;
for(int i=1;i<=n;i++){
int x=i;
for(int j=1;j<=tot;j++){
ci[j][i]=ci[j][i-1];
while(x%pr[j]==0)x/=pr[j],ci[j][i]++;
}
jc[i]=1ll*jc[i-1]*x%mod;
ijc[i]=qp(jc[i],phi-1);
}
}
inline int C(int n,int m){
if(n<m)return 0;
int ret=1ll*jc[n]*ijc[m]%mod*ijc[n-m]%mod;
for(int i=1;i<=tot;i++)
ret=1ll*ret*qp(pr[i],ci[i][n]-ci[i][m]-ci[i][n-m])%mod;
return ret;
}
signed main(){
cin>>n>>mod>>l>>r;
init();
int ans=0;
for(int i=0;i<=n;i++)
(ans+=1ll*C(n,i)*(C(i,(i-l)>>1)-C(i,(i-r-1)>>1)+mod)%mod)%=mod;
cout<<(ans+mod)%mod;
}
Stranger Trees
加强:\(n\le 8000\)
至少选 \(i\) 条树边的方案数为 \(g_i\),那么 \(f_i\) 根据二项式反演求得。
不难想到这样一个问题:已经选了 \(i\) 条树边,故现在有 \(n-i\) 个连通块,再连 \(n-1-i\) 条边构成不同有标号无根树的个数是几?如果我们知道了这个问题的答案,那就是 \(g_i\) 了(因为我们只是钦定至少有 \(i\) 条树边,生成树是否还有就不确定)
有标号无根树提示我们 Prufer 序列,根据经典算法可以知道当初始连通块数目为 \(k\) 时是 \(n^{k-2}\prod s_i\),其中 \(s_i\) 表示每个连通块的大小。(多嘴一句,\(k=n\) 时化简是 \(n^{n-1}\)。)
所以关键在于求 \(\prod s_i\)。由于又有树的条件,可以考虑树形 dp。
设 \(f[u][i][j]\) 表示 \(u\) 为根的子树划分成 \(i\) 个连通块,\(u\) 所在连通块大小为 \(j\) 的所有方案的 \(\prod s_i\) 之和(\(j\) 还未乘上)。小编估摸这个状态设计的想出是因为:(1)只设 \(u\) 和 \(i\) 转移不了(2)\(j\) 所在的连通块的大小必须参与转移。
转移方程 \(\forall v\in Son(u),f'[u][i][j]\gets \sum_{x\ge 1}\sum_{y\ge 1} (f[u][i-x+1][j-y]+f[u][i-x][j])\cdot f[v][x][y]\)。根据树形 dp 的复杂度分析方法,可知复杂度是 \(O(n^3)\)。
接下来盯着 \(\prod s_i\) 看,这是我们进一步优化的切入点,它的组合意义是从每个连通块中任选一个点的方案数。因此问题变成每个连通块中选谁,也即 \(u\) 所在的连通块所选点是否在 \(u\) 子树中。
设 \(f[u][i][0/1]\) 表示 \(u\) 子树,\(i\) 个连通块,\(u\) 所在连通块所选点不在/在子树内。
\(f'[u][i][0]\gets f[u][i-x][0]\cdot f[v][x][1]\)
\(f'[u][i][1]\gets f[u][i-x][1]\cdot f[v][x][1]\)
\(f'[u][i][0]\gets f[u][i-x+1][0]\cdot f[v][x][0]\)
\(f'[u][i][1]\gets f[u][i-x+1][0]\cdot f[v][x][1]+f[u][i-x+1][1]\cdot f[v][x][0]\)
复盘:
- 立方方法中 \(f\) 设为“\(j\) 还未乘上”令状态仍处在商榷阶段,巧妙!
- 组合意义优化的实质,是转化为“选”的问题。“选”——选谁?谁选不选?后者就是 0/1 问题了(\(O(1)\))。
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x/10)print(x/10);
putchar(x%10+48);
}
const int N=8005,mod=1e9+7;
int n,g[N][2],siz[N],_n[N],jc[N],ijc[N];
vector<int>G[N],f[N][2];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
int qp(int a,int b){int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;return c;}
void dfs(int x,int p){
siz[x]=1;
f[x][0].resize(2),f[x][1].resize(2);f[x][0][1]=f[x][1][1]=1;
for(int y:G[x])if(y^p){
dfs(y,x);
for(int i=1;i<=siz[x];i++)
g[i][0]=f[x][0][i],g[i][1]= f[x][1][i],f[x][0][i]=f[x][1][i]=0;
siz[x]+=siz[y];
f[x][0].resize(siz[x]+1),f[x][1].resize(siz[x]+1);
for(int j=1;j<=siz[y];j++){
for(int i=1;i<=siz[x]-siz[y];i++){
//树形背包一律采用刷表法 instead of 填表法,可显著减小常数!
add(f[x][0][i+j],1ll*g[i][0]*f[y][1][j]%mod);
add(f[x][1][i+j],1ll*g[i][1]*f[y][1][j]%mod);
add(f[x][0][i+j-1],1ll*g[i][0]*f[y][0][j]%mod);
add(f[x][1][i+j-1],(1ll*g[i][0]*f[y][1][j]+1ll*g[i][1]*f[y][0][j])%mod);
}
}
for(int i=1;i<=siz[x];i++)g[i][0]=g[i][1]=0;
}
}
inline int C(int n,int m){return 1ll*jc[n]*ijc[m]%mod*ijc[n-m]%mod;}
int main(){
n=read();
for(int i=1,u,v;i<n;i++)
u=read(),v=read(),G[u].push_back(v),G[v].push_back(u);
dfs(1,0);
int invn=qp(n,mod-2);
_n[0]=1; for(int i=1;i<=n;i++)_n[i]=1ll*_n[i-1]*n%mod;
jc[0]=ijc[0]=1; for(int i=1;i<=n;i++)jc[i]=1ll*jc[i-1]*i%mod,ijc[i]=qp(jc[i],mod-2);
for(int i=0,ans;i<n;i++){
ans=0;
for(int j=i;j<n;j++)
add(ans,((j-i&1)?mod-1ll:1ll)*C(j,i)%mod*
(n-j-2==-1?invn:_n[n-j-2])%mod*f[1][1][n-j]%mod);
print(ans),putchar(' ');
}
}
10.12(广铁一中模拟赛)
T1 序列

#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=1e5+5;
int n,a[N],p[N],p2[N];
vector<pair<int,int> >A;
set<int>B;
set<int>::iterator pos;
long long solve(){
long long ret=0;
for(int i=0;i<A.size();i++)ret+=abs(A[i].first-A[i].second);
sort(A.begin(),A.end(),[&](pair<int,int>x,pair<int,int>y){
if(x.first<x.second&&y.first<y.second)return a[x.first]<a[y.first];
if(x.first>=x.second&&y.first>=y.second)return a[x.first]>a[y.first];
return (x.first<x.second)<(y.first<y.second);
});
for(int i=0;i<A.size();i++){
if(A[i].first>A[i].second){
pos=prev(B.upper_bound(A[i].first));
p[*pos]=a[A[i].first];
B.erase(pos);
}
else {
pos=B.lower_bound(A[i].first);
p[*pos]=a[A[i].first];
B.erase(pos);
}
}
A.clear(),B.clear();
return ret;
}
int main(){
n=read();
int u=0;
for(int i=1;i<=n;i++)a[i]=read(),u+=a[i]&1;
if(n&1){
if(u>n/2){
for(int i=1;i<=n;i+=2)B.insert(i);
for(int i=1,o=1;i<=n;i++)if(a[i]&1)A.emplace_back(i,o),o+=2;
}
else {
for(int i=2;i<=n;i+=2)B.insert(i);
for(int i=1,o=2;i<=n;i++)if(a[i]&1)A.emplace_back(i,o),o+=2;
}
solve();
if(u>n/2){
for(int i=2;i<=n;i+=2)B.insert(i);
for(int i=1,o=2;i<=n;i++)if(!(a[i]&1))A.emplace_back(i,o),o+=2;
}
else {
for(int i=1;i<=n;i+=2)B.insert(i);
for(int i=1,o=1;i<=n;i++)if(!(a[i]&1))A.emplace_back(i,o),o+=2;
}
solve();
}
else {
long long cmp1=0,cmp2=0;
for(int i=1;i<=n;i+=2)B.insert(i);
for(int i=1,o=1;i<=n;i++)if(a[i]&1)A.emplace_back(i,o),o+=2;
cmp1+=solve();
for(int i=2;i<=n;i+=2)B.insert(i);
for(int i=1,o=2;i<=n;i++)if(!(a[i]&1))A.emplace_back(i,o),o+=2;
cmp1+=solve();
for(int i=1;i<=n;i++)p2[i]=p[i];
for(int i=2;i<=n;i+=2)B.insert(i);
for(int i=1,o=2;i<=n;i++)if(a[i]&1)A.emplace_back(i,o),o+=2;
cmp2+=solve();
for(int i=1;i<=n;i+=2)B.insert(i);
for(int i=1,o=1;i<=n;i++)if(!(a[i]&1))A.emplace_back(i,o),o+=2;
cmp2+=solve();
if(cmp1<cmp2)swap(p,p2);
else if(cmp1==cmp2){
bool flag=1;
for(int i=1;i<=n;i++){
if(p2[i]<p[i]){flag=0;break;}
else if(p2[i]>p[i])break;
}
if(!flag)swap(p,p2);
}
}
for(int i=1;i<=n;i++)printf("%d ",p[i]);
}
T2 游戏


从全新视角看待子游戏:进入一棵树走完看做是切换胜负局面的手段。
如果走完这棵树之后回到大本营时的局面是一个必胜局面,但在此条件下递推出的这棵树的根节点是一个必败局面,说明我们当前(还没有去这棵树的根节点时)是一个通往必败局面的局面,即必胜局面。开始必胜,后来也必胜,记作 (1,1);
如果走完这棵树之后回到大本营时的局面是一个必胜局面,而在此条件下递推出的这棵树的根节点是一个必胜局面,说明我们当前(还没有去这棵树的根节点时)是一个通往必胜局面的局面,即必败局面。开始必败,后来却必胜,记作 (0,1);
依此类推,有 (1,0) 和 (0,0)。
如果把每一棵树次第加入并考虑只有当前这些树时的状态,则可以发现,(1,1) 表示无论添加这棵树之前是什么状态,添加之后都是必胜态。这里的“必胜态”等都是针对先手而言,下同。
同理,有 (0,0) 表示无论添加这棵树之前是什么状态,添加之后都是必败态;(0,1) 会恰好翻转状态;而 (1,0) 不造成任何改变。
可以发现,加入树的次序对最终必胜还是必败没有影响,是确定的。起初,没有树时,是个必败态。
综上,先手必败当且仅当不存在 (1,1) 且 (0,1) 的个数是偶数。
答案即是 \(2^{c(0,0)+c(1,0)}\sum_{i=0}^{c(0,1)/2}{c(0,1)\choose 2i}\)。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5,mod=998244353;
int m,n,ijc[N],jc[N],sg[N];
vector<int>G[N];
int C(int n,int m){return 1ll*jc[n]*ijc[m]%mod*ijc[n-m]%mod;}
inline int qp(int a,int b){int c=1;
for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;return c;}
int mex(vector<int>&vec){
if(vec.empty())return 0;
sort(vec.begin(),vec.end());
if(vec[0])return 0;
for(int i=1;i<vec.size();i++)if(vec[i]>vec[i-1]+1)return vec[i-1]+1;
return vec.back()+1;
}
void dfs(int x,int val){
vector<int>vec;
bool isl=1;
for(int y:G[x]){
dfs(y,val);
vec.push_back(sg[y]);
isl=0;
}
if(isl)sg[x]=val;
else sg[x]=mex(vec);
}
int main(){
scanf("%d",&m);
jc[0]=ijc[0]=1;
for(int i=1;i<=m;i++)jc[i]=jc[i-1]*1ll*i%mod,ijc[i]=qp(jc[i],mod-2);
int c00=0,c10=0,c01=0,c11=0;
for(int i=1;i<=m;i++){
scanf("%d",&n);
for(int j=1;j<=n;j++)G[j].clear();
for(int j=2,p;j<=n;j++){
scanf("%d",&p);
G[p].push_back(j);
}
int sg1,sg0;
dfs(1,0),sg1=sg[1];
dfs(1,1),sg0=sg[1];
if(sg1&&sg0)c00++;
if(sg1&&!sg0)c01++;
if(sg0&&!sg1)c10++;
if(!sg0&&!sg1)c11++;
}
int ans=0;//cout<<c00<<c10<<c01<<c11;
for(int i=0;i<=c01;i+=2)ans=(ans+C(c01,i))%mod;//cout<<ans;
cout<<((qp(2,m)-1ll*qp(2,c00+c10)*ans%mod)%mod+mod)%mod<<'\n';
}
T3 灯

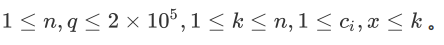
显然是一道 DS 题。想了一会可以发现没有什么数据结构能维护这种东西,故考虑暴力算法(分块等)。分块好像也不行,另一种分块——根号分治貌似很可行,因为每个点只属于一个开关,所以对于小开关暴力,大开关怎么弄一下按说能做出来。
然后由于我们要统计亮灯的连通块数,联想到树上点边容斥(链是特殊的树),所求即为 **点亮的点数 - 相邻两个都点亮的对数**。前者极易统计,考虑后者。
对于所控制的灯数小于根号的开关的状态反转,我们可以就维护一个序列 $lit$ 代表每个位置是否点亮,然后每次枚举这个开关的灯看一下左右相邻位置是否点亮然后直接统计。当然,对于所有的开关,我们都要预处理出只打开它时的相邻点亮对数。
对于所控制的灯数大于根号的开关,我们可以发现跟它中灯相邻的灯要么是大开关的灯要么是小开关的灯。如果是大开关的灯,由于大开关总共就根号个,所以存一下是哪些,到时暴力判断每一个是否点亮然后计数器加上 **只打开他俩开关时的相邻点亮对数** 即可,后者需要预处理。如果是小开关的灯,我们考虑在小开关进行遍历的时候就把这个大开关上打上标记,代表改变大开关的状态会带来的影响,这样便可以在大开关的状态切换时直接加上这个变化量(具体的实现细节不难自己摸索)。
至此我们在 $O(q\sqrt n)$ 的时间内解决了这个问题。
```cpp
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x<0){putchar('-'),print(-x);return;}
if(x/10)print(x/10);
putchar(x%10+48);
}
const int N=2e5+5;
int n,q,K,tot,B,bel[N],r[500][500],cnt[N],tag[N],ibig[N];
bool bk[N],lit[N];
vector<int>own[N],big,adj[N];
set<int>tmp;
int main(){
n=read(),q=read(),K=read(),B=sqrt(n);
for(int i=1;i<=n;i++)bel[i]=read(),own[bel[i]].push_back(i);
for(int i=1;i<=K;i++){
if(own[i].size()>B)ibig[i]=big.size(),big.push_back(i);
for(int j=1;j<own[i].size();j++)
if(own[i][j]==own[i][j-1]+1)cnt[i]++;
}
int i_1=0,i_2=0,all=0;
for(int i:big){
for(int j:own[i])bk[j]=1;
i_2=0;
for(int j:big){
if(i^j)for(int k:own[j])r[i_1][i_2]+=bk[k-1]+bk[k+1];
i_2++;
}
for(int j:own[i])bk[j]=0;
i_1++;
tmp.clear();
for(int j:own[i]){
if(j>1)tmp.insert(bel[j-1]);
if(j<n)tmp.insert(bel[j+1]);
}
for(int j:tmp)if(own[j].size()>B&&i!=j)adj[i].emplace_back(j);
}
int ans=0;
for(int x;q--;){
x=read(),lit[x]=!lit[x];
int F=1;
if(!lit[x])F=-1;
if(own[x].size()<=B){
for(int i:own[x]){
if(i>1&&bel[i-1]!=x){
if(own[bel[i-1]].size()<=B)ans+=F*lit[bel[i-1]];
else {
if(lit[bel[i-1]])ans+=F,tag[bel[i-1]]-=F;
else tag[bel[i-1]]+=F;
}
}
if(i<n&&bel[i+1]!=x){
if(own[bel[i+1]].size()<=B)ans+=F*lit[bel[i+1]];
else {
if(lit[bel[i+1]])ans+=F,tag[bel[i+1]]-=F;
else tag[bel[i+1]]+=F;
}
}
}
}
else {
ans+=tag[x],tag[x]=-tag[x];
for(int i:adj[x])if(lit[i])ans+=F*r[ibig[x]][ibig[i]];
}
all+=F*own[x].size(),ans+=F*cnt[x];
print(all-ans),putchar('\n');
}
}
T4 比赛
10.15
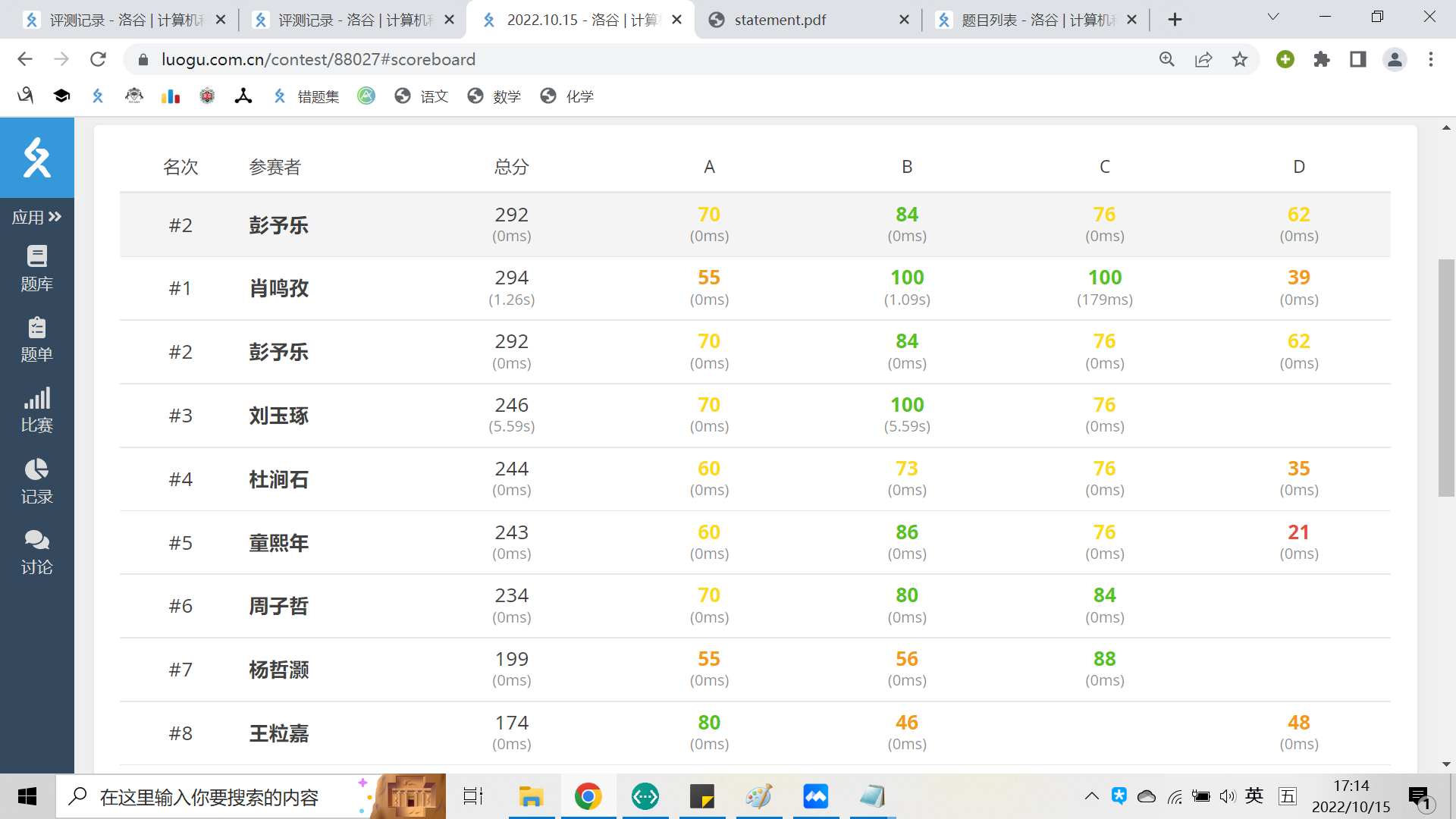
今天的题不算很精,T3 记个题解思路就好了。至于 T4,边分治一时也学不来,就不订了。
T1 是有向基环树上判一些东西,比较简单,但是我写挂了 30 分,变成 70 分了,经查明原因,是基环树的环的断环成链再加倍的方向搞反了,就是有向环的方向弄反了。
T2 是一道比较清新的题但比较简单,感觉略达不到 NOIPT2 的难度,简要地是求长 5e5 的小写字符串中形如 “114514” 的子序列个数(“小 Y 认为子序列 q 形如当且仅当:|q| = 6 且 对于任意 1 ⩽ i, j ⩽ 6,有 [qi = qj ] = [ti = tj ]”)。短暂思考后可以发现枚举 5 的位置然后预处理 dp 统计左边 114 的个数和右边 14 的个数就可以了。主要矛盾在于卡空间,可以交换一下循环顺序然后省掉一维,这样就是时间 \(O(n\Sigma^2)\)、空间 \(O(n\Sigma)\) 的。不过我因为有一个常没卡到位所以 T 了16分,考完之后发现其实有一个清空 dp 数组可以省略没有影响,就 A 了。
T3 是一道输出 YES/NO 却没有捆绑测试的题(我一开始选择全部输出 NO 结果分数不好看,恰巧老师通知延长比赛时间就又交了一发全输出 YES 的,喜提 76;反正正式考试谁也没分,与我无关),然后题面的约束还少了一句话。总之题意是给你一个位运算表达式,由 &,|,!,ai(1<=i<=n<=15) 和空格构成(空格处在每个运算符的两侧),让你对每个 \(i∈[0,2^n)\) 判一下表达式的真假,表达式可能长达 2e6。做法其实比较暴力,就是按照 | 把表达式分割成若干段,每一段等于真当且仅当 a1~a15 满足一种状态,就可以用一个三进制数来状压各 ai 的真假,1表示必须真,2表示必须假,0表示随便。那么可以用段数个三进制数来刻画这个表达式,当任意一种关系被满足时都可以使表达式真。然后从这些状态可以递推(把0换成1和2)出每个三进制数怎么样,就完了。
T4 的话,题意就是一个边带权树,从每个点 u 出发的 \(\max\{(u到v路径上所有边的权值最小值)\times (u到v路径上的点数)|v=1,2,...,n\}\)。然后我打了个暴力和一个星图特殊性质,居然能有62
10.18
四道没一道会做,垫底场。
T1
求单位圆上 n 个不同点中任选三个构成的三角形的九点圆圆心期望坐标。三角形的九点圆是三边中点的外接圆。\(n\le 5\times 10^5\)
这个题默认你知道九点圆圆心在三角形外心和垂心的中点上,光是这一点我就不知道。然后,求垂心 \(H\),单位圆上三点的垂心为 \(H=A+B+C\),证明:\(\overrightarrow{AH}\cdot {\overrightarrow{BC}}=0\),所以 \((\overrightarrow{OH}-\overrightarrow{OA})\cdot (\overrightarrow{OC}-\overrightarrow{OB})=0\),同理 \((\overrightarrow{OH}-\overrightarrow{OB})\cdot (\overrightarrow{OC}-\overrightarrow{OA})=0\)、\((\overrightarrow{OH}-\overrightarrow{OC})\cdot (\overrightarrow{OB}-\overrightarrow{OA})=0\),三式相加,得 $$\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$$,即 \(H=A+B+C\)。后面的统计部分略。
T2
题面非常晦涩,题目非常困难,场上无人 AC。
T3
题面非常晦涩,题目非常困难,场上无人 AC。
T4
\(n\le 10^6\)
由于我并没有做好题目难度不随顺序而递增的准备,所以看完 T2,T3 后绝望的我无心对付这刻板印象中的压轴题,而且题目中还有“哈密顿路”这种陌生字眼,“NPC问题”更是让人知难而退。然而这题确实本场的次简单题。
其实这个哈密顿路跟欧拉路就是一个是点的一笔画一个是边的一笔画,没什么可怕的。如果什么操作都不干,就是要求点的一笔画。但我们知道点的一笔画就是求欧拉序的方法,然后欧拉序必须回到根节点,但是哈密顿路不一定,所以只需要找一条最长的路径,可以少走这一路径。然后我们发现每个点可能不只经过一次,一个观察是图中故弄玄虚的操作带来的功能其实就是经过原来的节点时你可以绕开走,那也相当于每个点允许经过的次数 +1。我们知道进行操作的次数等于最终哈密顿路的点数减去 n,而我们知道刚才所说的方法一定是使得哈密顿路长度最短的方法。于是只需要求树的直径,而最小操作次数就是 (2n-1)-n-(树的直径的点数-1),其中 2n-1 是欧拉序的长度,n 是一开始每个点允许经过一次,树的直径的点数 -1 就是到最后可以剩下不用走的欧拉序长度。化简就是 (n-直径的点数)。构造应该不必多言。
10.23
T1

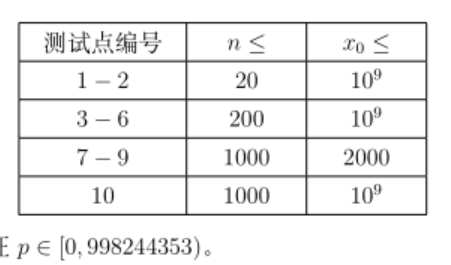
没做出的签到。事实上 brute force 是对的,但是我去写了个 2^n 的更 brute force 的 brute force,但凡我多留点时间出来把第三档部分分写了也能AC;不过没分析出就是没分析出啊……
#include <bits/stdc++.h>
using namespace std;
const int N=1005,mod=998244353;
int X,n,p,ans;
unordered_map<int,int>f,t;
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline int calc(int x){if(!x)return 0;int r=0;while(!(x&1))r++,x>>=1;return r;}
int main(){
freopen("qaq.in","r",stdin);freopen("qaq.out","w",stdout);
cin>>X>>n>>p;
f[X]=1;
for(int i=1;i<=n;f=t,t.clear(),i++)
for(auto j:f)add(t[j.first>>1],1ll*j.second*p%mod),add(t[j.first+1],1ll*j.second*(mod+1-p)%mod);
for(auto i:f)add(ans,1ll*i.second*calc(i.first)%mod);
cout<<ans;
}
//复杂度分析
//对于0个/2操作的,有O(n)个+1操作;对于1个/2操作的,有O(n)个+1操作;……
//由于最多O(log)次/2,所以map中至多O(nlogn)个数
T2
给定 \(n\),求 \(\max/\min_{x_i\in N_+,\sum x_i=n} \sum d(x_i)\)(d(x)为x的约数个数)。
这题我是场上为数不多的几个做出来的,还不错。
max就不说了。
题解可能是把我的过程结论化了(我是打了一点表),说是什么哥德巴赫猜想(被我打表发现了)。具体就是你打一个表(用 \(f_i=\min(f_j+f_{i-j})\) 递推),发现每个数的答案只会是 3,4,5,3的情况是n-1是质数,4的情况是它是俩质数和,5的情况是它是一个质数的平方和一个质数;再还有一种情况是从n-1的答案+1转移过来。质数只需要处理前500个(也可能远远用不着)。感觉还是题解靠谱些,虽然依赖样例的不断WA讨论到了每种情况,但还是有失清晰性。
#include "game.h"
#include <bits/stdc++.h>
using namespace std;
map<int,int>tmpmin,tmpmax;
int p[600]={质数表,不放了,怕博客炸了};
bool isprime(int n){
for(int j=2;j*j<=n;j++)if(n%j==0)return 0;
return 1;
}
int D(int n){
int cnt=0;
for(int j=1;j*j<=n;j++)if(n%j==0){
cnt++;
if(j*j!=n)cnt++;
}
return cnt;
}
pair<map<int,int>,map<int,int> >solve(int n){
tmpmax[1]=n;
tmpmin.clear();
if(isprime(n)){
tmpmin[n]++;
}
else if(isprime(n-1)){
tmpmin[1]++;
tmpmin[n-1]++;
}
else{
int S=sqrt(n);if(S*S==n&&isprime(S)){
tmpmin[n]++;
return make_pair(tmpmin,tmpmax);
}
for(int i=1;i<=500&&p[i]<n;i++){
if(isprime(n-p[i])){
tmpmin[p[i]]++,tmpmin[n-p[i]]++;
return make_pair(tmpmin,tmpmax);
}
}
for(int i=1;i<=500&&p[i]*p[i]<=n;i++){
if(isprime(n-p[i]*p[i])){
tmpmin[p[i]*p[i]]++,tmpmin[n-p[i]*p[i]]++;
if(D(n)<5){
tmpmin.clear(),tmpmin[n]++;
}
return make_pair(tmpmin,tmpmax);
}
}
tmpmin[n]++;
if(D(n)>5){
pair<map<int,int>,map<int,int> >ooo=solve(n-1);
ooo.first[1]++;ooo.second[1]=n;
return ooo;
}
}
return make_pair(tmpmin,tmpmax);
}
T3
有两棵树①和②,1是根,初始都只有1在里面,依次同时加入2,3,...,接在各自的某个节点下面,当每棵树点数是偶数时,假如是i,那就输出1 ~ i这i个数两两组对后每一对(记为(u,v))的min(dep①(lca①(u,v)),dep②(lca②(u,v)))之和的最小值,dep定义为1到它的路径上点数。\(n\le 2\cdot 10^5\)
注:这里只有45pts的平方做法,正解没听懂,也觉得对于我的水平而言意义不大(码量很大)
我们从贡献的角度看每一个点,对于一个确定的组对方案,答案是所有深度相同的两异树点子树内
完整包含的点对的交集的大小 之和。
//原本想要写一下为什么是对的,但是写不下去了。只说一个,multiset里面存的其实代表的其实是深度相同“两个异树点”,然后里面都是leftover;后续如果匹配上了就删掉,否则又多了一个leftover。每次往根跑的路径上的所有点你都有机会去匹配掉leftover让ans++,那你会说难道同一个点可以同时跟很多个点匹配吗?不是的,你比如说一个原来是leftover的4先在一轮有几个被5匹配走了,又在一轮有几个被6匹配走了,这不是说4真的匹配上了5和6两个数,而是6匹配的时候把5之前匹配的掠夺走了,由于5和6它们匹配走的一定是一个前缀(从根开始的连续向下路径),而5的肯定比6的短,那6匹配到5之前的痕迹处时由于leftover已经被5吃了所以它会没有也就是会insert一个leftover,这可以看做是6其实匹配上了,而5没有匹配上,再懂不懂,不懂就感性理解吧,我写不下去了
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=2e5+5;
int n,ans,fa1[N],fa2[N],dep1[N],dep2[N];
struct pairhash {
public:
template <typename T, typename U>
size_t operator()(const pair<T, U> &x) const{
return hash<T>()((x.first-x.second)<<5) ^ hash<U>()(x.second<<1)+hash<T>()(x.first>>1) & hash<U>()(x.second<<1);
}
};
unordered_set<pair<int,int>,pairhash>st;
int main(){
freopen("qwq.in","r",stdin);freopen("qwq.out","w",stdout);
n=read();
st.insert(make_pair(1,1));
for(int i=2,u,v;i<=n;i++){
fa1[i]=read(),fa2[i]=read();
dep1[i]=dep1[fa1[i]]+1,dep2[i]=dep2[fa2[i]]+1;
u=v=i;
while(dep1[u]>dep2[v])u=fa1[u];
while(dep2[v]>dep1[u])v=fa2[v];
for(;u;u=fa1[u],v=fa2[v]){
if(st.count(make_pair(u,v)))st.erase(st.find(make_pair(u,v))),ans++;
else st.insert(make_pair(u,v));
}
if(!(i&1))cout<<ans<<'\n';
}
}
10.24
T1
错题,略。
T2
给你一个每个点度 \(\ge 4\) 的无向图,要求你给每条边染色,使得每个点的邻边的颜色集的大小恰好为 2。\(5\le n\le 5\times 10^5,2n\le m\le 10^6\)
根据套路题条件反射第33条,我们先将原图转为欧拉图,然后进行边的 dfs 序列上的黑白染色。然后单独取出所有黑边,对于每个黑边构成的联通块,将其中所有边染成一种独一无二的颜色;白边同理。这样一来,每个点就会被至少进两次出两次,因此颜色A和颜色B(化名)会都至少各2次,且恰好只有这两种颜色。
本题坑点:dfs同色边的连通块时,要在不包含0的图(原图)中进行,否则,0所在的那个同色边的连通块可能会在原图中体现为不连通。而需要在含0的那个图里找欧回。
#include <bits/stdc++.h>
#define pb emplace_back
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x/10)print(x/10);
putchar(x%10+48);
}void print(int x,char c){print(x),putchar(c);}
const int N=2e6+5;
int n,m,dfc,cnt,O,dfn[N],col[N];
bool del[N],vis[N];
vector<pii>G[N/4],E[N/4];
void euler(int x){
while(!E[x].empty()){
if(del[E[x].back().se]){E[x].pop_back();continue;}
del[E[x].back().se]=1;
dfn[E[x].back().se]=dfc,dfc^=1;
int t=E[x].back().fi;
E[x].pop_back();
euler(t);
}
}
void dfs(int x){
vis[x]=1;
for(auto y:G[x])if(dfn[y.se]==O&&!col[y.se]){
col[y.se]=cnt;
dfs(y.fi);
}
}
int main(){
freopen("next.in","r",stdin);freopen("next.out","w",stdout);
cout<<"1\n";
n=read(),m=read();
for(int i=1,u,v;i<=m;i++)u=read(),v=read(),G[u].pb(v,i),G[v].pb(u,i);
for(int i=0;i<=n;i++)E[i]=G[i];
for(int i=1,o=m;i<=n;i++)if(E[i].size()&1)E[0].pb(i,++o),E[i].pb(0,o);
for(int i=1;i<=n;i++)euler(i);
for(int i=1;i<=n;i++)if(!vis[i])cnt++,dfs(i);
O=1;
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++)if(!vis[i])cnt++,dfs(i);
print(cnt,'\n');
for(int i=1;i<=m;i++)print(col[i],' ');
}
T3
【交互题】一棵 bfs 序为 1,2,...,n 的树,你每次可以询问
vector<int>query(vector<pair<int,int> >tmp),返回 tmp 中每一点对的两点间路径上节点数。你可以询问 1 次,点对数量不能超过 n。你需要实现int solve(int n),返回 \(\sum_{i=1}^n (i的子树内最深的节点的深度)\)(深度定义为 1 到 i 路径的点数)。\(n\le 2000\)
由于 bfs 序为 1 ~ n,不妨让每一层的点自左而右递增排列,比较好看 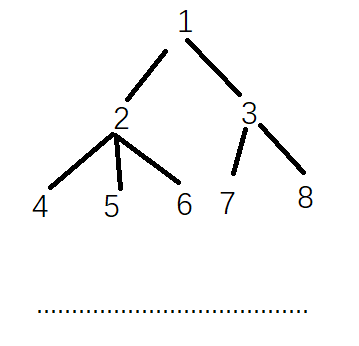
然后我们按照 bfs 序(也就是1到n的顺序)加入点,那么自然地想到怎么获取每个点的深度,那就要知道哪一段代表同一深度,发现性质,同层两点i-1和i之间的距离一定是偶数,上层i-1和该层i之间的距离一定是奇数。同层两点i-1和i之间的距离除以2还可推出它们的lca。经过不复杂的处理可以得到答案。
#include "willbe.h"
#include <bits/stdc++.h>
using namespace std;
const int N=2005;
int id[N];
vector<int>f[N];
int solve(const int n,const int m,const int k){
vector<pair<int,int> >tmp;
for(int i=1;i<n;i++)tmp.emplace_back(i,i+1);
vector<int>rep=query(tmp);
f[1].emplace_back(1);
for(int i=2,d=1;i<=n;i++){
if(rep[i-2]&1)for(int j=d-1;j>d-rep[i-2]/2;j--)f[j][++id[j]]=d;
else for(int j=d++;j;j--)f[j][id[j]=0]=d;
f[d].emplace_back(d);
}
int sum=0;
for(int i=1;i<=n;i++)for(int j:f[i])sum+=j;
return sum;
}
T4


由于是两元异或和最值,肯定在 01trie 上。我们先考虑 n 阶完全图,边权为两数的 xor,点有颜色,那么对于此图中的一环,其中的最大边 (u,v,w),若 u,v 同色,则必不可取,可以删之,若异色,则环中必有另一对异色边且边权不超过 w,亦可删之;归纳可知,只有最小生成树才有用。结合“01trie”,那就是01trie上的每个叶子上有若干(0/1/多)个点,求这些点的最小生成树,那么可以类似线段树合并的方式从局部逐渐推到全局;利用启发式合并思想可以做到 \(O(n\log n\log A)\)。针对查询而言,我们最直接的思路是遍历改点邻边然后更新一个 multiset,那我们会担忧超时的风险,比如菊花图?理性分析可知,每个点只会在它在01trie上对应的叶子的所有祖先处有可能合并(连一条边),那么每个点的度数是 \(O(\log A)\) 的,自然刚才查询算法的复杂度也是 \(O(\log A\log n)\)/次 的。总复杂度 \(O((n+q)\log n\log A)\)。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
register char ch=getchar();register int x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void print(int x){
if(x/10)print(x/10);
putchar(x%10+48);
}
const int N=2e5+5;
int n,q,tot=1,a[N],c[N],siz[N*30],trie[N*30][2];
vector<int>vec[N*30],ve[N*30],G[N];
multiset<int>st;
void ins(int x,int id){
int rt=1;siz[1]++;
for(int i=29;~i;i--){
int b=x>>i&1;
if(!trie[rt][b])trie[rt][b]=++tot;
rt=trie[rt][b];siz[rt]++;
}
ve[rt].push_back(id);
}
int qry(int x){
int rt=1;
for(int i=29;~i;i--){
int b=x>>i&1;
if(siz[trie[rt][b]])rt=trie[rt][b];
else rt=trie[rt][!b];
}
return ve[rt][0];
}
inline void adde(int u,int v){
G[u].push_back(v),G[v].push_back(u);
if(c[u]^c[v])st.insert(a[u]^a[v]);
}
void dfs(int x,int dep){
if(trie[x][0])dfs(trie[x][0],dep-1);
if(trie[x][1])dfs(trie[x][1],dep-1);
if(!trie[x][0]&&!trie[x][1]){
vec[x]=ve[x];
for(int i=1;i<vec[x].size();i++)adde(vec[x][i-1],vec[x][i]);
return;
}
if(!trie[x][1]){swap(vec[x],vec[trie[x][0]]);return;}
if(!trie[x][0]){swap(vec[x],vec[trie[x][1]]);return;}
if(vec[trie[x][0]].size()>vec[trie[x][1]].size())swap(vec[trie[x][0]],vec[trie[x][1]]);
int oo=2e9,uu=0,vv=0,u;
for(int v:vec[trie[x][0]]){
u=qry(a[v]^(1<<(dep-1)));
if((a[u]^a[v])<oo)oo=a[u]^a[v],uu=u,vv=v;
}
adde(uu,vv);
for(int j:vec[trie[x][0]])vec[trie[x][1]].emplace_back(j);
swap(vec[x],vec[trie[x][1]]);
}
int main(){
freopen("who.in","r",stdin);freopen("who.out","w",stdout);
n=read(),q=read();
for(int i=1;i<=n;i++)a[i]=read(),ins(a[i],i);
for(int i=1;i<=n;i++)c[i]=read();
dfs(1,30);
for(int x,y;q--;){
x=read(),y=read();
for(int z:G[x]){
if((c[x]^c[z])&&!(y^c[z]))st.erase(a[x]^a[z]);
if(!(c[x]^c[z])&&(y^c[z]))st.insert(a[x]^a[z]);
}
c[x]=y;
print(*st.begin()),putchar('\n');
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号