小记：整数划分dp

【问题引入】

求 \(\LARGE{|}\) \(\large{\{}\) \(\{x_1,x_2,...\}\mid x_i\in[1,K],\sum x_i=N\) \(\large{\}}\) \(\LARGE{|}\)（其中 \(\{x_1,x_2,...\}\) 为可重集。

我们发现最终的划分可以表示为一个阶梯的形状，如下：

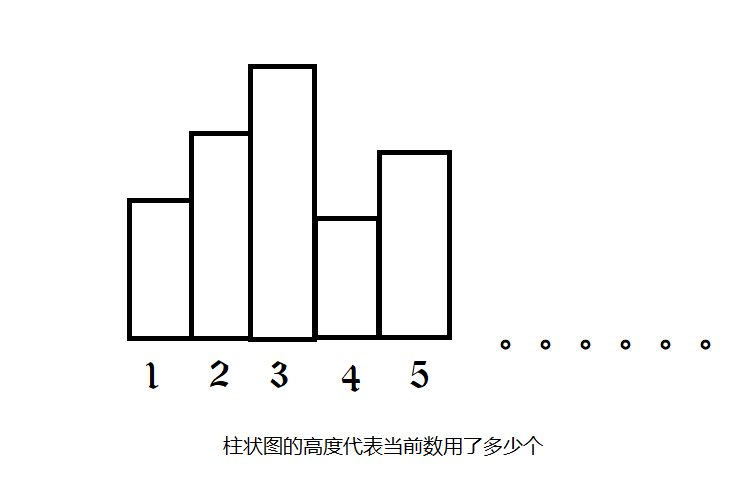
那么是直接依次枚举每个柱状图的高度转移么？不行啊。
我们考虑柱状图的生成过程，演示如下图：

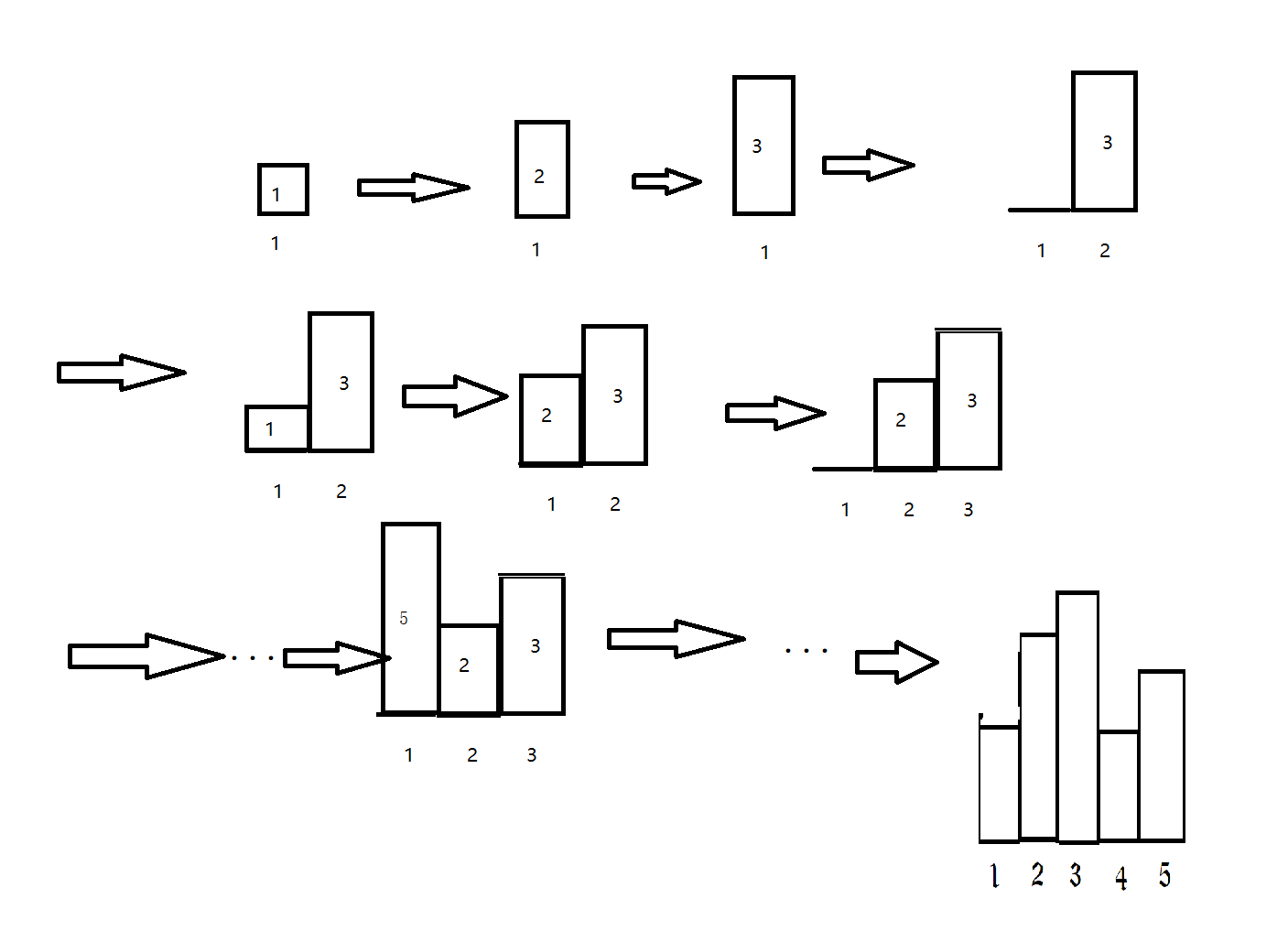
也就是说，我们其实只用使用两种操作就可生成任意柱状图（数的划分）。

1. 将当前的每个数值的权重 +1
2. 把 “1” 的个数 +1

【直接应用】小 Y 的背包计数问题
这个题目不仅仅是整数划分，因为每个数字是有次数限制的。
通过某种思考方式，我们可以踩到根号分治上：
我们发现 \(>\sqrt n\) 的数是没有次数限制的（因为最多使用(背包容量÷数值)个,必不超过限制），而 \(\le \sqrt n\) 的数种类数少，可以使用暴力的 dp。
整体来说，我们想要把这两部分单独计算，分别计算出 \(F_1(V)\) 表示背包容量为 \(V\)、只使用 \(1\sim \sqrt n\) 的数情况下的方案数，\(F_2(V)\) 表示背包容量为 \(V\)、只使用 \(\sqrt n+1\sim n\) 的数情况下的方案数，那么我们 \(O(n)\) 枚举把背包的多少容积分配给第一部分，多少容积分配给第二部分从而合并答案即可。现在就需要求出所谓的 \(F_1,F_2\)。

具体来说：

• 对于 \(1\sim\sqrt n\) 的部分，我们轻易得出递推式

\[f[i][j]=\sum_{k\in[0,i]}f[i-1][j-ki] \]

转移复杂度较高，但是明显有 \(j-ki\equiv j\pmod i\)，因此用许多 vector 做成的桶来按序存储所有 \(\bmod i\) 下相同的 \(j\) 对应的 \(f[i-1][j]\)，那么我们需要的就是当前 \(f[i-1][j-0\cdot i],f[i-1][j-1\cdot i],f[i-1][j-2\cdot i],...,f[i-1][j-i\cdot i]\)，也即 \(j\bmod i\) 号桶里的最后 \(i+1\) 个值的和，区间求和我们可以通过就地维护前缀和来实现。

• 对于 \(\sqrt n+1\sim n\) 的部分，我们按照整数划分 dp 的做法做就好了。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5,mod=23333333;
int n,B,f[405][N],g[405][N],h[N];
vector<int>buc[N];
int main(){
	cin>>n,B=sqrt(n);
	g[0][0]=h[0]=1;
	for(int i=1;i<=B;i++){
		for(int j=1;j<=n;j++){
			if(j>=i)g[i][j]=g[i][j-i];
			if(j>=B+1)(g[i][j]+=g[i-1][j-B-1])%=mod;
			h[j]=(h[j]+g[i][j])%mod;
		}
	}
	f[0][0]=1;
	for(int i=1;i<=B;i++){
		for(int j=0;j<=n;j++)buc[j].clear();
		for(int j=0;j<=n;j++){
			int tmp=((buc[j%i].empty()?0:buc[j%i].back())+f[i-1][j])%mod;
			buc[j%i].push_back(tmp);
			if(!buc[j%i].empty())f[i][j]=buc[j%i].back()-(buc[j%i].size()<i+2?0:buc[j%i][buc[j%i].size()-i-2]);
		}
	}
	int ans=0;
	for(int i=0;i<=n;i++)ans=(ans+1ll*h[i]*f[B][n-i]%mod)%mod;
	cout<<ans;
}