NOIP%9.7

战况：

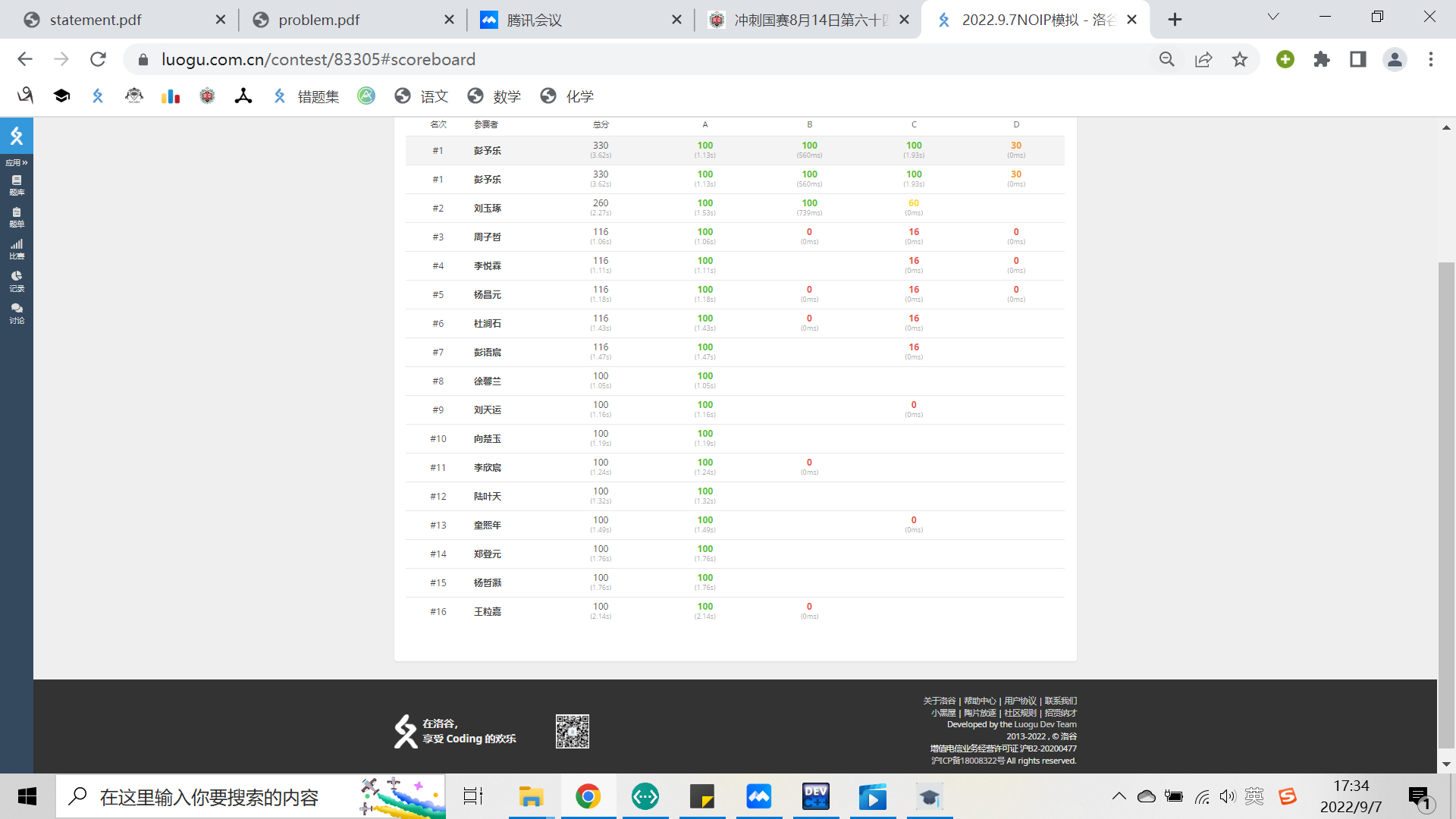
T1
签到题，略。
T2

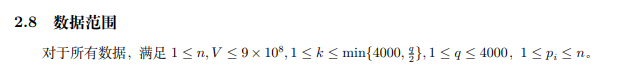
稍加思考不难解决题。
我们发现其实本质上每一次修改操作是雷同的，考虑求出进行 \(i\) 次雷同操作的时候，各个位置的期望查询到的值是多少。
那么就相当于在依次的 1~q-k-1 个查询中选 k-1 个不同的位置放上查询（因为最后一个查询固定在了 q-k 处），“放上查询”的意思是等1~【这个位置】的修改进行完毕后查一次。
那么就可用 f[i][j] 表示前 i 个修改中放上 j 个查询，期望的期望查询和是多少。
f[i][j]=C(i-1,j-1)÷C(i,j)×(val[j]+f[i-1][j-1])+C(i-1,j)÷C(i,j)×f[i-1][j];
其中 val[i] 为刚才说到的进行若干次（实时维护）修改之后 p[i] 位置的期望单次查询值。

#include <bits/stdc++.h>
using namespace std;
inline int read(){
	register char ch=getchar();register int x=0;
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
typedef long long ll;
const int N=4005,mod=998244353,I2=(mod+1)/2;
int n,q,k,V,p[N],val[N],f[N][N],jc[N],ijc[N];
int qp(int a,int b){
	int c=1;
	for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
	return c;
}
inline int C(int n,int m){return n<m?0:1ll*jc[n]*ijc[m]%mod*ijc[n-m]%mod;}
inline int iC(int n,int m){return n<m?0:1ll*jc[m]*jc[n-m]%mod*ijc[n]%mod;}
int main(){
	n=read(),q=read(),k=read(),V=read();
	for(int i=1;i<=k;i++)p[i]=read();
	ijc[0]=jc[0]=1;
	for(int i=1;i<=q;i++)jc[i]=1ll*jc[i-1]*i%mod;
	ijc[q]=qp(jc[q],mod-2);
	for(int i=q-1;i;i--)ijc[i]=ijc[i+1]*(i+1ll)%mod;
	int IN2=qp(1ll*n*n%mod,mod-2);
	for(int i=1;i<=q-k;i++){
		for(int j=1;j<=k;j++){
			ll psb=(2ll*p[j]*(n-p[j]+1)-1)%mod*IN2%mod,tmp=1ll*I2*(1+V+val[j])%mod;
			val[j]=(psb*tmp%mod+(mod+1-psb)*val[j]%mod)%mod;
		}
		for(int j=1;j<=min(i,k);j++){
			f[i][j]=(1ll*C(i-1,j-1)*iC(i,j)%mod*((val[j]+f[i-1][j-1])%mod)%mod+
			1ll*C(i-1,j)*iC(i,j)%mod*f[i-1][j]%mod)%mod;
		}
	}
	cout<<(f[q-k-1][k-1]+val[k])%mod;
}

T3

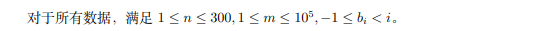
居然有原题。之前 Accoder NOI 上的一场模拟赛，还是 zzy 讲的题。
考虑区间 dp，设 \(f[l,r,v]\) 表示只考虑 \([l,r]\) 区间内的填数方案，且只能填 \(\le v\) 的答案。
由于【大小关系】是本题的一个特征，而它没有在状态设计当中体现，所以在转移当中须体现。故考虑：枚举最大值。
当最大值 \(<v\) 时，\(f[l,r,v]\gets f[l,r,v-1]\)
当最大值 \(=v\) 时（重点），

• 枚举最大值位置 \(i\)
• \(i\) 不能作为最大值位置的情况有二，只要不是这两种情况就可以把 \(f[l,i-1,v]\times f[i+1,r,v-1]\) 累加进答案。一是 \(b_i\ge l\)，这说明左边、区间内有比他大的数；二是，如果有一个 \((b_j,j](j>i,b_j\ne -1)\) 区间覆盖了 \(i\)，那么：要么 \(b_j\ge l\)，说明 \(a_i\le a_j< a_{b_j}\)，\(i\) 不可能是最大值，要么 \(b_j<l\)，说明在算 \(j\) 的时候就已经把 \(a_i=v\) 的情况算过了，只是“名义上 \(a_i\) 不是最大值”。你会发现这是一种十二分巧妙的方法，并且难以被替代或改动。

那么我们就需要求 \(f[1,n,m]\)，这个的复杂度是 \(O(n^3m)\) 的，其中 \(n^3\) 是区间 dp。
考虑到数列中的数种类最多只有 \(n\) 种，所以其实这个 \(m\) 是没用的，可以组合数去掉。如果我们算出 \(h[v]\) 表示 \(1\sim v\) 都使用到，且 \(a_i\le v\) 的方案数，那么 \(ans=\sum\binom{m}{i}h[i]\)。设 \(g[v]=f[1,n,v]\)，那么，\(h[v]\) 可以容斥计算出来，是 \(\sum_{j=1}^v(-1)^{v-j}\)，可以用二项式反演证得。总复杂度是常数极小的 \(O(n^4)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read(){
	register char ch=getchar();register int x=0,f=1;
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x*f;
}
const ll mod=1e9+7;
const int N=305,kM=100005;
int n,m,a[N],bann[N*4][N];
ll sum,jc[kM],ijc[kM],inv[kM],f[N][N][N],g[N],h[N];
inline ll C(int n,int m) {return jc[n]*ijc[m]%mod*ijc[n-m]%mod;}
ll calc_f(int l,int r,int v,int dep=0) {
	if(l>r) return 1;
	if(v==0) return 0;
	if(~f[l][r][v]) return f[l][r][v];
	ll &res=f[l][r][v]=calc_f(l,r,v-1,dep+1);
	int *ban=bann[dep];
	for(int i=l;i<=r+1;++i) ban[i]=0;
	for(int i=r;i>=l;--i) {
		ban[i]+=ban[i+1];
		if(!ban[i]&&a[i]<l) (res+=calc_f(l,i-1,v,dep+1)*calc_f(i+1,r,v-1,dep+1))%=mod;
		if(a[i]!=-1) ++ban[i],--ban[a[i]];
	}
	return res%=mod;
}
signed main() {
	inv[1]=jc[0]=ijc[0]=1;
	for(int i=2;i<kM;++i) inv[i]=mod-mod/i*inv[mod%i]%mod;
	for(int i=1;i<kM;++i) jc[i]=jc[i-1]*i%mod,ijc[i]=ijc[i-1]*inv[i]%mod;
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>a[i];
	memset(f,-1,sizeof(f));
	if(m<=n) cout<<calc_f(1,n,m)<<endl;
	else {
		for(int i=1;i<=n;++i) g[i]=calc_f(1,n,i);
		for(int i=1;i<=n;++i) for(int j=1;j<=i;++j)
			(h[i]+=(((i-j)&1)?(mod-1ll):1ll)*C(i,j)%mod*g[j])%=mod;
		ll ans=0;
		for(int i=1;i<=n;++i) (ans+=C(m,i)*h[i])%=mod;
		cout<<ans<<endl;
	}
}

T4

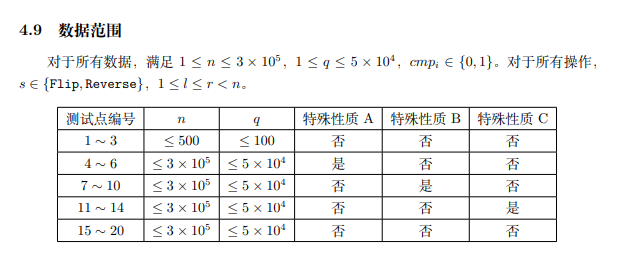
这个题使用动态 dp+线段树+平衡树可以很简单地维护，然而——我早已忘记怎么打 Splay 了，故只能做到 50pts（考试的时候有 20pts 本来可以用线段树的没有想到很好的解决办法）。一年半之前学的 Splay，当时觉得忒麻烦，所以练了几道题就一直丢下不碰了，现在忘得一干二净。

upd:
在李老师的强力鼓动下，鄙人决定还是尽快把 T4 订了。花了半个下午重学 Splay，但是还是对区间翻转以及该怎么维护线段树能维护的那些东西一脸茫然。在阅览了《维护数列》最高赞题解的代码后，勉强明白了一些，经过为期一天的曲折摸索，我终于按照原来 6×6 的矩阵的 ddp 把它写了出来，这时我已经很自豪地知道了 Splay 是怎么维护区间翻转以及区间元素和之类的东西了。由于对自己过于自信，我让李老师把已经结束订正的比赛延后了，此时已经凌晨 12 点。不过交上去只有 TLE 15pts，这时我才意识到后面的大样例还没测。不幸的是，suffix3.in 大样例就让我直接跑到 20s 多，真是见鬼了。对矩乘卡了一下常，到了 16s。接下来便束手无策了。
由于下发题解中写的是 3×3 的矩阵，而我也知道 6×6 的转移其实只有奇偶性是 cmp[i] 的列才 \(\ne 0\)，也就是说其实可以优化成 3×3 的。第二天早上起来就把 3×3 的方程推了出来，然而 was dismayed to see that 方程涉及到了 cmp[i+1]，这意味着修改的时候还要特判端点处附近的细节，哦天！一个 Splay 小白又鼓起勇气开始倒腾，经过漫长的编写和调试，编译后发现过不了最小的样例。调了一会发现是空节点(0)会被修改，改了之后过掉了最小样例，但是第一个大样例过不去了。又调了两个小时，最后发现是一个 ! 打掉了……好在功夫不负有心人，后面的大洋里都一顺溜过了，终于 A 掉了这个题，消除了我对如果今天还调不完该怎么叫李老师把比赛再延一会儿的担忧。
不辜负这次漫长的攻坚战，详详细细写一篇题解。

一个很自然的想法是探究到底是什么因素影响了两个相邻的后缀 \(i\) 和 \(i+1\) 的排名 \(cmp\)。
不妨考虑 \(rk_i<rk_{i+1}\) 的情况。第一种情况是 \(s_i<s_{i+1}\)；第二种情况是 \(s_i=s_{i+1}\)，那么还可以 \(s_{i+1}=s_{i+2}\) 这样一直下去，不难发现起决定因素的就是往后第一个不等于 \(s_{i}\) 的数是比 \(s_i\) 小还是大，如果是小就 \(rk_i>rk_{i+1}\)，否则 \(rk_i<rk_{i+1}\)。
所以很自然就可以以这个作为要素进行 dp。我是怎么想到 dp 的呢，是因为一开始想打个暴力，却发现 n=500 没办法 \(3^n\) 枚举啊^_^||，但是再没有更低档的暴力了，说明出题人肯定认为 n=500 不难做，那就意味着需要 dp 了。然后我们刚才说到利用往后的第一个不等于 \(s_i\) 的数与 \(s_i\) 的大小关系作为 dp 要素进行 dp，所以不难想到 \(f[i][j][0/1](i\in [1,n],j\in \{0,1,2\})\) 表示 \(s_i=j\)，且 往后的第一个不等于 \(s_i\) 的数 \(<\)(0) 还是 \(>\)(1) \(j\)。
暴力的转移类似这样：

for(int i=n-1;i;i--){
	for(int j=0;j<3;j++){
		if(cmp[i])f[i][j][1]=(f[i+1][j][1]+(j<2?(f[i+1][j+1][0]+f[i+1][j+1][1])%mod+(j<1?f[i+1][j+2][0]+f[i+1][j+2][1]:0)%mod:0)%mod)%mod,f[i][j][0]=0;
		else f[i][j][0]=(f[i+1][j][0]+(j?(f[i+1][j-1][0]+f[i+1][j-1][1])%mod+(j>1?f[i+1][j-2][0]+f[i+1][j-2][1]:0)%mod:0)%mod)%mod,f[i][j][1]=0;
	}
}
cout<<((long long)f[1][0][0]+f[1][0][1]+f[1][1][0]+f[1][1][1]+f[1][2][0]+f[1][2][1])%mod<<'\n';

这个家伙写成矩阵形式：

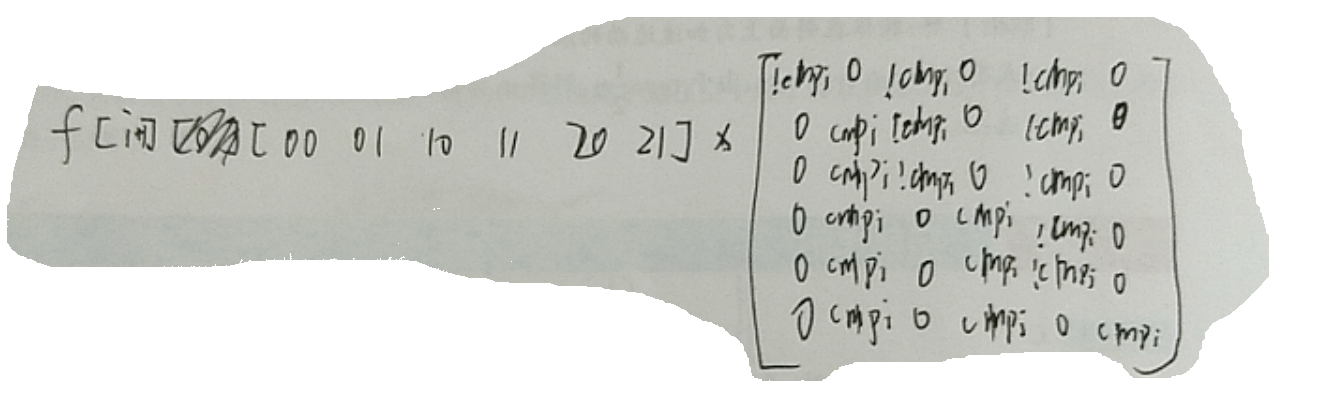
使用 Splay 维护区间矩阵连乘积（注意，是从右往左乘的）。维护方法为：

struct node:
  int fa,ch[2],siz,val;
  mat2 cur,a,b,ab,mycur,mya,myb,myab;
  int rev,fl,cmp;
//mat2 为一个 6*6 的矩阵结构体
//cur为当前的状态下子树中的乘积
//a为reverse当前子树后子树中的乘积
//b为flip当前子树后子树中的乘积
//ab为flip&reverse当前子树后子树中的乘积（不难发现ba和ab是等价的,所以没有ba）
//mycur为当前的状态下当前节点的自身矩阵
//mya为reverse当前子树后当前节点的自身矩阵
//myb为flip当前子树后当前节点的自身矩阵
//myab为flip&reverse当前子树后当前节点的自身矩阵
//rev和fl分别为reverse和flip的懒标记，cmp为当前节点的当前自身cmp值

这样的好处在于：
flip 的时候只需要 swap(cur,b),swap(ab,a),swap(mycur,myb),swap(myab,mya) 并打上 fl 标记，reverse 的时候只需要 swap(cur,a),swap(ab,b),swap(mycur,mya),swap(myab,myb) 即可。

不过这样是会超时的，主要原因是：矩阵转移要 \(6^3\)。
我们试图把它优化到 \(3^3\)。新的矩阵转移：

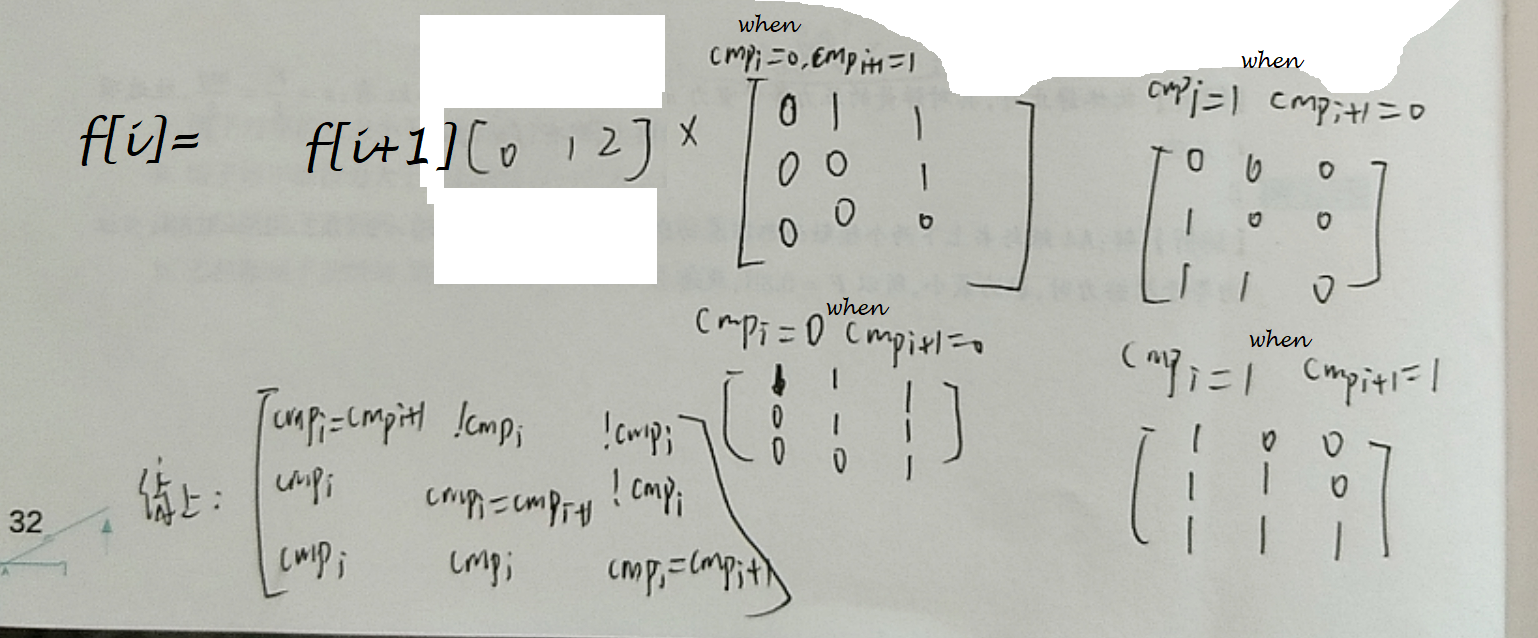
然后就要考虑这个 \(cmp[i]\ne cmp[i+1]\) 怎么去维护。
insert() 是这样的写法：

inline void insert(int x,int o0=-1,int o=0,int o1=-1){//cmp[i-1],cmp[i],cmp[i+1]
	int cur=root,p=0;
	while(cur&&t[cur].val!=x){
		pushdown(cur);
		p=cur;
		cur=t[cur].ch[x>t[cur].val];
	}
	t[++tot].val=x,t[tot].siz=1,t[tot].cmp=o;
	if(o0==-1)w[++tw]=varn,t[tot].cur=t[tot].a=t[tot].b=t[tot].ab=t[tot].mycur=t[tot].mya=t[tot].myb=t[tot].myab=tw;
	else {
		w[t[tot].cur=++tw]=w[t[tot].mycur=++tw]=unu[o][o1];
		w[t[tot].a=++tw]=w[t[tot].mya=++tw]=unu[o][o0];
		w[t[tot].b=++tw]=w[t[tot].myb=++tw]=unu[!o][!o1];
		w[t[tot].ab=++tw]=w[t[tot].myab=++tw]=unu[!o][!o0];
	}
	if(p)t[tot].fa=p,t[p].ch[x>t[p].val]=tot;
	splay(tot);
}
//相当于a,b,ab是默认对应的相邻元素(i+1或i-1)跟着i一起flip/reverse
//由此会造成一些矛盾，矛盾发生在reverse/flip时的l-1,l,r,r+1四个位置上，需要特判

对于reverse，我们首先把 \([l-1,l-1]\) split 出来，获取它的 cmp 值 _c，把 \([r+1,r+1]\) split 出来，获取它的 cmp 值 c_，把 \([l,l]\) 和 \([r,r]\) split 出来，获取 cmp 值 cl,cr。对于 split 出的 \([l,l]\) 节点，你要知道reverse[l,r]只有它会变到跟r+1相邻，所以w[t[k].a]=w[t[k].mya]=unu[t[k].cmp][c_], w[t[k].ab]=w[t[k].myab]=unu[!t[k].cmp][!c_];这样由于在reverse[l,r]的标记下传之后是会swap(b,ab),swap(cur,a)的，所以可以保证新的ab和cur是对的。那么对于 r,l-1,r+1 以及 flip[l,r]的处理也类似，就不放了，大家自己看代码吧。

#include <bits/stdc++.h>
#define oo(i,j) ret.a[i][j]=(A.a[i][0]*B.a[0][j]+A.a[i][1]*B.a[1][j]+A.a[i][2]*B.a[2][j])%mod
using namespace std;
inline int read(){
	register char ch=getchar();register int x=0;
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
void print(int x){
	if(x/10)print(x/10);
	putchar(x%10+48);
}
const int N=3e5+5,mod=1e9+7;
int n,q,tw,tot,root,cmp[N];
struct mat1{int a[3];int sum(){return ((long long)a[0]+a[1]+a[2])%mod;}}ini;
struct mat2{long long a[3][3];}unu[2][2],varn,w[8*N];
char op[2];
inline mat2 operator*(mat2 A,mat2 B){
	mat2 ret;
	oo(0,0),oo(0,1),oo(0,2);
	oo(1,0),oo(1,1),oo(1,2);
	oo(2,0),oo(2,1),oo(2,2);
	return ret;
}
inline mat1 operator*(mat1 A,mat2 B){
	mat1 ret;
	for(int i=0;i<3;i++)
		ret.a[i]=(A.a[0]*B.a[0][i]+A.a[1]*B.a[1][i]+A.a[2]*B.a[2][i])%mod;
	return ret;
}
inline void pr(int o){
	for(int i=0;i<3;i++,cerr<<'\n')for(int j=0;j<3;j++)cerr<<w[o].a[i][j];
}
struct node {
	int fa,ch[2],siz,val,cur,a,b,ab,mycur,mya,myb,myab;
	//a:rev b:flip
	int rev,fl,cmp;
	node(){ch[0]=ch[1]=0;}
}t[N];
inline int chk(int k){return t[t[k].fa].ch[1]==k;}
inline void pushup(int k){
	w[t[k].a]=(w[t[t[k].ch[0]].a]*w[t[k].mya])*w[t[t[k].ch[1]].a];
	w[t[k].cur]=(w[t[t[k].ch[1]].cur]*w[t[k].mycur])*w[t[t[k].ch[0]].cur];
	w[t[k].b]=(w[t[t[k].ch[1]].b]*w[t[k].myb])*w[t[t[k].ch[0]].b];
	w[t[k].ab]=(w[t[t[k].ch[0]].ab]*w[t[k].myab])*w[t[t[k].ch[1]].ab];
	t[k].siz=t[t[k].ch[0]].siz+t[t[k].ch[1]].siz+1;
}
inline void pushdown(int k){
	if(t[k].rev){
		if(t[k].ch[0])
		t[t[k].ch[0]].rev^=1,
		swap(t[t[k].ch[0]].ab,t[t[k].ch[0]].b),
		swap(t[t[k].ch[0]].a,t[t[k].ch[0]].cur),
		swap(t[t[k].ch[0]].myab,t[t[k].ch[0]].myb),
		swap(t[t[k].ch[0]].mya,t[t[k].ch[0]].mycur),
		swap(t[t[k].ch[0]].ch[0],t[t[k].ch[0]].ch[1]);
		if(t[k].ch[1])
		t[t[k].ch[1]].rev^=1,
		swap(t[t[k].ch[1]].ab,t[t[k].ch[1]].b),
		swap(t[t[k].ch[1]].a,t[t[k].ch[1]].cur),
		swap(t[t[k].ch[1]].myab,t[t[k].ch[1]].myb),
		swap(t[t[k].ch[1]].mya,t[t[k].ch[1]].mycur),
		swap(t[t[k].ch[1]].ch[0],t[t[k].ch[1]].ch[1]);
		t[k].rev=0;
	}
	if(t[k].fl){
		if(t[k].ch[0])
		t[t[k].ch[0]].fl^=1,t[t[k].ch[0]].cmp^=1,
		swap(t[t[k].ch[0]].ab,t[t[k].ch[0]].a),
		swap(t[t[k].ch[0]].b,t[t[k].ch[0]].cur),
		swap(t[t[k].ch[0]].myab,t[t[k].ch[0]].mya),
		swap(t[t[k].ch[0]].myb,t[t[k].ch[0]].mycur);
		if(t[k].ch[1])
		t[t[k].ch[1]].fl^=1,t[t[k].ch[1]].cmp^=1,
		swap(t[t[k].ch[1]].ab,t[t[k].ch[1]].a),
		swap(t[t[k].ch[1]].b,t[t[k].ch[1]].cur),
		swap(t[t[k].ch[1]].myab,t[t[k].ch[1]].mya),
		swap(t[t[k].ch[1]].myb,t[t[k].ch[1]].mycur);
		t[k].fl=0;
	}
}
inline void rotate(int x){
	int y=t[x].fa,z=t[y].fa,k=chk(x);
	t[y].ch[k]=t[x].ch[k^1],t[t[x].ch[k^1]].fa=y;
	t[z].ch[chk(y)]=x,t[x].fa=z;
	t[x].ch[k^1]=y,t[y].fa=x;
	pushup(y),pushup(x);
}
inline void splay(int x,int goal=0){
	while(t[x].fa!=goal){
		int y=t[x].fa,z=t[y].fa;
		if(z!=goal){
			if(chk(x)==chk(y))rotate(y);
			else rotate(x);
		}
		rotate(x);
	}
	if(!goal)root=x;
}
inline int kth(int x){
	if(x<1||x>n+2)return 0;
	int k=root;
	while(1){
		pushdown(k);
		if(t[t[k].ch[0]].siz>=x)k=t[k].ch[0];
		else if(t[t[k].ch[0]].siz+1>=x)return k;
		else x-=t[t[k].ch[0]].siz+1,k=t[k].ch[1];
	}
	return k;
}
inline int split(int l,int r){
	int x=kth(l),y=kth(r+2);
	if(!x||!y)return 0;
	splay(x),splay(y,x);
	return t[y].ch[0];
}
inline void reverse(int l,int r){
	int k;
	k=split(l-1,l-1);
	int _c=t[k].cmp;
	k=split(r+1,r+1);
	int c_=t[k].cmp;
	k=split(l,l);
	int cl=t[k].cmp;
	w[t[k].a]=w[t[k].mya]=unu[t[k].cmp][c_];
	w[t[k].ab]=w[t[k].myab]=unu[!t[k].cmp][!c_];
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(r,r);
	int cr=t[k].cmp;
	w[t[k].cur]=w[t[k].mycur]=unu[t[k].cmp][_c];
	w[t[k].b]=w[t[k].myb]=unu[!t[k].cmp][!_c];
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(l-1,l-1);
	if(k)
	w[t[k].cur]=w[t[k].mycur]=unu[_c][cr],
	w[t[k].b]=w[t[k].myb]=unu[!_c][!cr],
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(r+1,r+1);
	if(k)
	w[t[k].a]=w[t[k].mya]=unu[c_][cl],
	w[t[k].ab]=w[t[k].myab]=unu[!c_][!cl],
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(l,r);
	t[k].rev^=1;//pr(t[k].cur);
	swap(t[k].a,t[k].cur);
	swap(t[k].ab,t[k].b);
	swap(t[k].mya,t[k].mycur);
	swap(t[k].myab,t[k].myb);
	swap(t[k].ch[0],t[k].ch[1]);
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
}
inline void flip(int l,int r){
	int k;
	k=split(l-1,l-1);
	int _c=t[k].cmp;
	k=split(r+1,r+1);
	int c_=t[k].cmp;
	k=split(l,l);
	int cl=t[k].cmp;
	w[t[k].ab]=w[t[k].myab]=unu[!t[k].cmp][_c];
	w[t[k].a]=w[t[k].mya]=unu[t[k].cmp][!_c];
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(r,r);
	int cr=t[k].cmp;
	w[t[k].cur]=w[t[k].mycur]=unu[t[k].cmp][!c_];
	w[t[k].b]=w[t[k].myb]=unu[!t[k].cmp][c_];
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(l-1,l-1);
	if(k)
	w[t[k].cur]=w[t[k].mycur]=unu[_c][!cl],
	w[t[k].b]=w[t[k].myb]=unu[!_c][cl],
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(r+1,r+1);
	if(k)
	w[t[k].a]=w[t[k].mya]=unu[c_][!cr],
	w[t[k].ab]=w[t[k].myab]=unu[!c_][cr],
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
	k=split(l,r);
	t[k].fl^=1,t[k].cmp^=1;
	swap(t[k].b,t[k].cur);
	swap(t[k].ab,t[k].a);
	swap(t[k].myb,t[k].mycur);
	swap(t[k].mya,t[k].myab);
	pushup(t[k].fa),pushup(t[t[k].fa].fa);
}
inline void insert(int x,int o0=-1,int o=0,int o1=-1){
	int cur=root,p=0;
	while(cur&&t[cur].val!=x){
		pushdown(cur);
		p=cur;
		cur=t[cur].ch[x>t[cur].val];
	}
	t[++tot].val=x,t[tot].siz=1,t[tot].cmp=o;
	if(o0==-1)w[++tw]=varn,t[tot].cur=t[tot].a=t[tot].b=t[tot].ab=t[tot].mycur=t[tot].mya=t[tot].myb=t[tot].myab=tw;
	else {
		w[t[tot].cur=++tw]=w[t[tot].mycur=++tw]=unu[o][o1];
		w[t[tot].a=++tw]=w[t[tot].mya=++tw]=unu[o][o0];
		w[t[tot].b=++tw]=w[t[tot].myb=++tw]=unu[!o][!o1];
		w[t[tot].ab=++tw]=w[t[tot].myab=++tw]=unu[!o][!o0];
	}
	if(p)t[tot].fa=p,t[p].ch[x>t[p].val]=tot;
	splay(tot);
}
int main(){
	//freopen("suffix2.in","r",stdin);freopen("suffix.out","w",stdout);
	ini.a[0]=ini.a[1]=ini.a[2]=1;
	varn.a[0][0]=varn.a[1][1]=varn.a[2][2]=1;
	for(int i=0;i<=1;i++)for(int j=0;j<=1;j++){
		unu[i][j].a[0][0]=unu[i][j].a[1][1]=unu[i][j].a[2][2]=i==j;
		unu[i][j].a[1][0]=unu[i][j].a[2][0]=unu[i][j].a[2][1]=i;
		unu[i][j].a[0][1]=unu[i][j].a[0][2]=unu[i][j].a[1][2]=!i;
	}
	w[t[0].cur=t[0].a=t[0].b=t[0].ab=t[0].mycur=t[0].mya=t[0].myb=t[0].myab=++tw]=varn;
	n=read(),q=read();
	insert(0),insert(n),insert(n+1);
	for(int i=1;i<n;i++)cmp[i]=read();
	for(int i=1;i<n;i++)insert(i,cmp[i-1],cmp[i],cmp[i+1]);//cerr<<"g";
	//for(int i=1;i<=tot;i++)cerr<<t[i].ch[0]<<t[i].ch[1]<<';';cerr<<((ini*((unu[2]*unu[0])*(unu[1]*unu[2]))).sum())<<' ';
	print((ini*w[t[split(1,n-1)].cur]).sum()),putchar('\n');cerr<<"j";
	for(int l,r;q--;){
		scanf("%s",op),l=read(),r=read();
		if(op[0]=='F')flip(l,r);
		else reverse(l,r);
		print((ini*w[t[split(1,n-1)].cur]).sum()),putchar('\n');
	}
}//200多行代码，你也该知道这题我写了多久