NOIP%9.3

第一场

A.一步之遥

按照一定顺序打印 \(n(n\le 9)\) 的全排列，使得相邻两个排列中，同一数字所在的两个位置相差 1。

标签：构造

签到题写假了，bewildered。
正确的做法是，现在已知 \(n=1\) 的答案是

1

那么 \(n=2\) 的答案是

2 1
1 2

那么 \(n=3\) 的答案是

3 2 1
2 3 1
2 1 3
1 2 3
1 3 2
3 1 2 

把 \(n=i-1\) 的每排原地复制 \((i+1)\) 次，如果是奇数排就从左到右插入 \(i\)，否则从右到左。

B.退位计划

给定一棵 \(n\) 个点的树，有 \(K\) 种颜色，求有多少种染色方案，使得每种颜色都被染到，任意一对相邻节点异色？\(n,K\le 10^6\)

标签：容斥

一、转化：只需每个节点跟父节点异色，所用颜色数 \(\le i\) 时，方案数为 \(g_i=i(i-1)^{n-1}\)，与树的形态无丝毫关系。
二、容斥：\(\sum_{i=1}^k(-1)^{K-i}\binom{K}{i}g_i\) 【这是为什么【坑待填】 话说学了二项式反演之后再看就很easy了，若\(h_i\)表示恰好使用 \(i\) 种颜色的方案数，那么 \(g_K=\sum_{i=1}^K \binom{K}{i}h_i\)，反演后得到 \(h_K=\sum_{i=1}^K (-1)^{K-i}\binom{K}{i}g_i\)】

C.退役之后

有一个 \(n\) 个点 \(m\) 条边的无向图，每条边 \((u_i,v_i)\) 有通过时间 \(w_i\)。厨师在 \(1\)，你是外卖小哥，初始在 \(1\)。依次下达 \(k\) 份订单，下达时间 \(s_i\)，顾客位置 \(u_i\)，厨师做好时间 \(t_i\)。你负责将所有订单划分成若干段，待每一段内的所有饭都做好之后按照订单的次序访问相应的顾客送饭给他们，然后回到 \(1\)，立即处理下一段。一个顾客的等待时间是送达时间和下单时间的差。你希望最小化等待最久的顾客的等待时间。\(n,k\le 1000,m\le 5000\)，其余 \(\le 10^9\)

很容易想到 dp，缺的就是一个段的价值怎么算。
发现直接算并不好算，考虑利用“最小化最大值”的经典套路——二分答案——进行转化。
那么显然就希望在前 \(i\) 个顾客等待时间不超过 \(mid\) 的前提下，最小化回到 \(1\) 的时刻。dp 这个时刻。那么需要知道一个区间内的顾客中等待时间最久的一位，不难发现这是可以离线处理出的。则转移方程式：(\(D[i]\) 为 \(1\) 依次到 \(1,2,...,i\) 所用时间，类似于一个前缀和，可以做减法求出两点间的用时)

\[f[i]=\min_{x\ge \max(f[j-1],t_i)+D[who[j][i]]-D[j]+dis[1][u_j]-s_{\small{who[j][i]}}}\{\max(f[j-1],t[i])+D[i]-D[j]+dis[1][u[j]]+dis[u[i]][1]\} \]

D.重在参与

有一条长为 \(S\) 的路，等距分布着 \(S+1\) 个点（包括端点），你在 0。有 \(n\) 个水坑，分别是 \(l_i\) 和 \(r_i\) 之间的线段，水坑互不重叠。\(l_i\) 和 \(r_i\) 都是干的，而 \((l_i,r_i)\) 中的点都是湿的，所以不能踩。但凡需要越过水坑都需要使用“跳跃”。跳一次走 \(\le D\) 的长度，花 \(T\) 的时间。正常走路 1 单位长度要 1 单位时间。（平地上也可以跳跃。）问最少多少时间到达 \(S\) 点。\(S,D,T\le 10^9,n\le 500\)

很明显是一个简单贪心，但是纯模拟会超时。我们的策略实际上就是：

• 若 \(D>T\)，则在平地上优先选择跳跃，如果会跳到水坑里就选择走路。
• 若 \(D\le T\)，则在平地上优先选择走路，但如果还有下一个水坑且当前点是最早的可以越过该水坑的点，则考虑跳跃。

可以发现只有每个水坑的左右边缘（\(l_i\) 和 \(r_i\)）是 crucial 的，其他的就是重复机械的工作，所以只需要求出 dp 辅助数组 \(w_{i,j}\) 表示两个关键点之间的最小时间，用 \(f_i=\min(f_j+w_{j,i})\) 递推即可。\(w_{i,j}\) 通过上一段的内容 \(O(n)\) 递推求得。

第二场

A.谜之阶乘

签到题，略。

B.子集

把自然数 \(1\sim n\) 分到 \(k\) 个集合里，每个集合中有 \(n/k\) 个元素，保证 \(k|n\)，要求每个集合中的元素和相等，请构造一种方案或报告无解。\(n\le 10^6\)

对于这个 \(k\times (n/k)\) 的长方形，不难想到分奇偶讨论。若长 \(n/k\) 是偶数，就可以第一列顺着 \(1\sim n\)、第二列倒着 \(2n\sim n+1\)、……
若长 \(n/k\) 是奇数，且宽 \(k\) 是偶数，会发现 \(k\nmid((1+n)n/2)\)，无解。
否则，就到了本题的难点，长宽都是奇数，可以想到先用第一种方法弄到还剩3列（\(1\sim 3k\)），这时该怎么构造呢？通过找规律可以发现

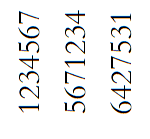
C.混凝土粉末

有一排 \(n\) 位置，\(q\) 个操作：

• 1 l r h：在 \([l,r]\) 位置每个位置再放上 \(h\) 个颜色 \(x\) 的方块，其中 \(x\) 为操作序号
• 2 x y：查询位置 \(x\) 的从下往上第 \(y\) 个方块的颜色

\(n\le 10^6,h\le 10^9,y\le 10^{18}\)

暴力主席树本来是可以拿 80+ 的，但是本地过了大样例交上去却是 RE 0pt，不知道是 accoders 评测机的问题还是什么其他原因。
这个题包含一个数据结构题转化套路：把区间离线扫描 + 切换主体（在操作序号上建立数据结构，如树状数组）。本来正常是依次处理询问，修改操作变成差分的一加一减，然后再位置序列上建立数据结构，这样就涉及到要查询最先在哪个询问的地方前缀 \(x\) 的高度和有 \(\ge y\) 了；由于回答操作序号为 \(i\) 的询问只和操作序号 \(<i\)、修改位置 \(<x\) 的修改操作有关（这里指的是差分的一加一减的修改操作），可以将所有修改操作和询问按照发生位置排个序，从左往右扫描，对于修改操作，令它原来的操作序号是 \(i\)，就把树状数组的 \(i\) 位置加上 \(\delta h\)，对于询问，就在树状数组上二分到最小的、前缀和 \(\ge y\) 的操作序号即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read(){
    register char ch=getchar();register ll x=0;
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return x;
}
void print(int x){
    if(x/10)print(x/10);
    putchar(x%10+48);
}
const int N=1e6+5;
int n,m,q;
ll c[N];
void add(int x,int y){for(;x<=q;x+=x&-x)c[x]+=y;}
ll ask(int x){ll s=0;for(;x;x-=x&-x)s+=c[x];return s;}
struct quer{int op,x;ll y;int id,ans;}qu[N*2];
signed main(){
    n=read(),q=read();
	ll y;
    for(int i=1,op,x,h;i<=q;i++){
        op=read();
        if(op==1)x=read(),y=read(),h=read(),qu[++m]=quer{1,x,h,i},qu[++m]=quer{2,(int)y+1,-h,i};
        else x=read(),y=read(),qu[++m]=quer{3,x,y,i};
    }
    sort(qu+1,qu+m+1,[](quer a,quer b){return a.x==b.x?a.op<b.op:a.x<b.x;});
    for(int i=1;i<=m;i++){
    	if(qu[i].op<=2)add(qu[i].id,qu[i].y);
    	else {
    		int L=0,R=q+1,mid;
    		while(L<R-1){
    			mid=L+R>>1;
    			if(ask(mid)>=qu[i].y)R=mid;
    			else L=mid;
    		}
    		if(R>qu[i].id)qu[i].ans=0;
    		else qu[i].ans=R;
    	}
    }
    sort(qu+1,qu+m+1,[](quer a,quer b){return a.id<b.id;});
    for(int i=1;i<=m;i++)if(qu[i].op==3)print(qu[i].ans),puts("");
}

D.排水系统

排水系统是一张 \(n\) 个点的 DAG，有 \(m\) 个入度为 0 的点，初始时有 1 的水量，除此以外所有点都有 \(\ge 1\) 的入度；有 \(r\) 个出度为 0 的点，除此以外所有店都有 \(\ge 2\) 的出度。每个点会将流到自己的水均分成【出度】份，并分给出边指向的点。目标是输出最后流到 \(r\) 个汇点的水量。然而每条边都有一定的可能性堵塞，第 \(i\) 条边有 \(a_i\over \sum a\) 的概率堵塞。你要对于每个汇点求出流到它的水量的期望。\(n,k\le 5\times 10^5,m+r\le n\)

考点：期望的可加性

一个暴力的想法是，把每条边算成堵塞的，每次跑一遍 DAG 递推，这样显然是不行的。这时我们发现，一条边 \((u,v)\) 堵塞造成的影响是流到 \(v\) 的水凭空 \(-\frac{flow_u}{d_u}\)，其他出点凭空 \(+(\frac{flow_u}{d_u-1}-\frac{flow_u}{d_u})\)（其中 \(flow_u\) 代表不堵塞的时候到达 \(u\) 的水量）。然后每次修改一条边就暴力跑一次，复杂度没变。不过由于每次都是重复地在跑 DAG 递推，而期望具有可加性，我们可以把所有凭空加加减减都改完再一次性跑一次 DAG 递推，是一样的。但是还有一个问题，就是菊花图这样的就会 TLE。我们可以进一步考虑更改一条边是等价于 \(u\) 凭空 \(+d_u(\frac{flow_u}{d_u-1}-\frac{flow_u}{d_u})\)，而 \(v\) 凭空 \(-\frac{flow_u}{d_u-1}\)。

#include <bits/stdc++.h>
using namespace std;
inline int read(){
	register char ch=getchar();register int x=0;
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
const int N=5e5+5,mod=998244353;
int n,m,r,k,flow[N],f[N],in[N];
struct edge {int u,v,w;}e[N];
vector<int>G[N];
queue<int>Q;
int qp(int a,int b=mod-2){
	int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
	return c;
}
int main(){
	n=read(),m=read(),r=read(),k=read();
	int sumw=0;
	for(int i=1;i<=k;i++){
		e[i].u=read(),e[i].v=read(),e[i].w=read();
		G[e[i].u].push_back(e[i].v),in[e[i].v]++;
		sumw=(sumw+e[i].w)%mod;
	}
	sumw=qp(sumw);
	for(int i=1;i<=m;i++)Q.push(i),flow[i]=f[i]=1;
	while(!Q.empty()){
		int x=Q.front();Q.pop();
		int tmp=1ll*qp(G[x].size())*flow[x]%mod;
		for(int y:G[x]){
			flow[y]=(flow[y]+tmp)%mod;
			if(!--in[y])Q.push(y);
		}
	}
	for(int i=1;i<=k;i++){
		int t2=1ll*qp(G[e[i].u].size()-1)*flow[e[i].u]%mod;
		f[e[i].u]=(f[e[i].u]+(1ll*t2*G[e[i].u].size()%mod-flow[e[i].u]+mod)%mod*(1ll*e[i].w*sumw%mod)%mod)%mod;
		f[e[i].v]=(f[e[i].v]+(mod-t2)%mod*(1ll*e[i].w*sumw%mod)%mod)%mod;
		in[e[i].v]++;
	}
	for(int i=1;i<=m;i++)Q.push(i);
	while(!Q.empty()){
		int x=Q.front();Q.pop();
		int tmp=1ll*qp(G[x].size())*f[x]%mod;
		for(int y:G[x]){
			f[y]=(f[y]+tmp)%mod;
			if(!--in[y])Q.push(y);
		}
	}
	for(int i=n-r+1;i<=n;i++)printf("%d ",f[i]);
}