平面分治（补）

之前没写过吗，补一下。
【模板】平面最近点对

分治处理 \(solve(l,mid),solve(mid+1,r)\)，令 \(d=\) 两者较小值，则只需要考虑和 \(mid\) 横向距离 \(<d\) 的点。

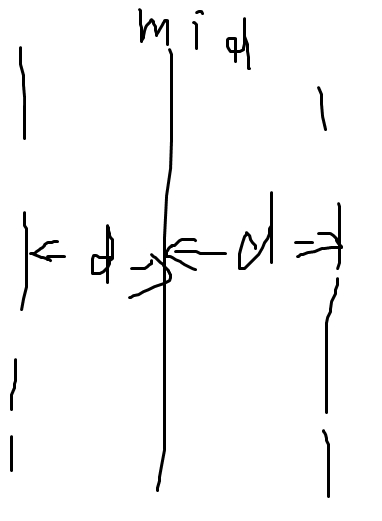
将长条虚线区间内的点按纵坐标排序，只有纵向距离 \(<d\) 的点对才是有用的。枚举 \(i\)，枚举到 \(j,dist(i,j)\ge d\) 就 break，即可 AC。

时间复杂度：\(O(n\log^2 n)\)（用 sort 排序）
复杂度证明：
(基本事实)长条内同侧两点距离 \(\ge d\)。
以 \(d\) 为阈值作出边长 \(d\) 的两个正方形，打虚线的线处空心（取不到）。

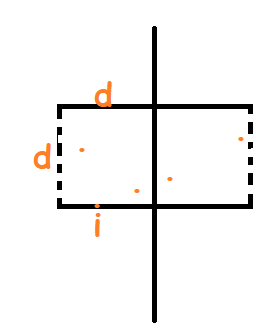
结合(基本事实)，可知每个正方形中至多有两个 \(j\) 的备选点。

【变式】最小三角形

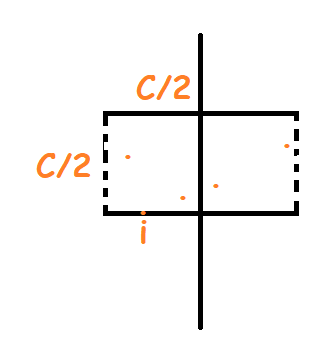
分治处理 \(C=\min(solve(l,mid),solve(mid+1,r))\)，并对 \(<C/2\) 的长条区间排序，不难发现由于 \(a+b\ge c(a\le b\le c),a+b+c=C\)，因此最长边 \(c\le C/2\)。
因此以 \(C/2\) 为边长作两个正方形。此时同侧两点的距离不一定 \(\ge C/2\)，但一个正方形中和 \(u\) 相距 \(<C/2\) 的点数量有限（1 个），因为如果有 2 个，就会在同侧产生周长 \(<C\) 的三角形。因此矩形中的点也屈指可数。

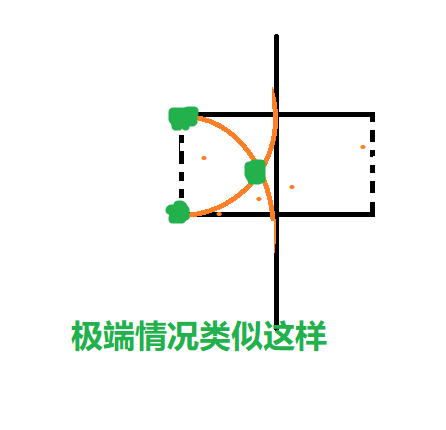
【总结】这类题目有一个共同点，就是暴力可以 AC，所以暴力就可以了。（暴力指一旦 dist>d 就 break）