平面图转对偶图
平面图转对偶图常用于解决平面图的最小割问题。
所谓平面图，就是能够在纸上画出来任意两边不在非顶点处相交的图。
对偶图是相对于一个平面图而言的。由于平面图的性质，你可以在纸上看到一些由边围成的许多封闭的面，假如把这些面编个号，看成节点，把两个面的交边映射到两个面所代表的节点之间的连边，则由面所代表的节点构成的新图叫做原平面图的对偶图。
举个例子，下面这个无向平面图和它的对偶图：
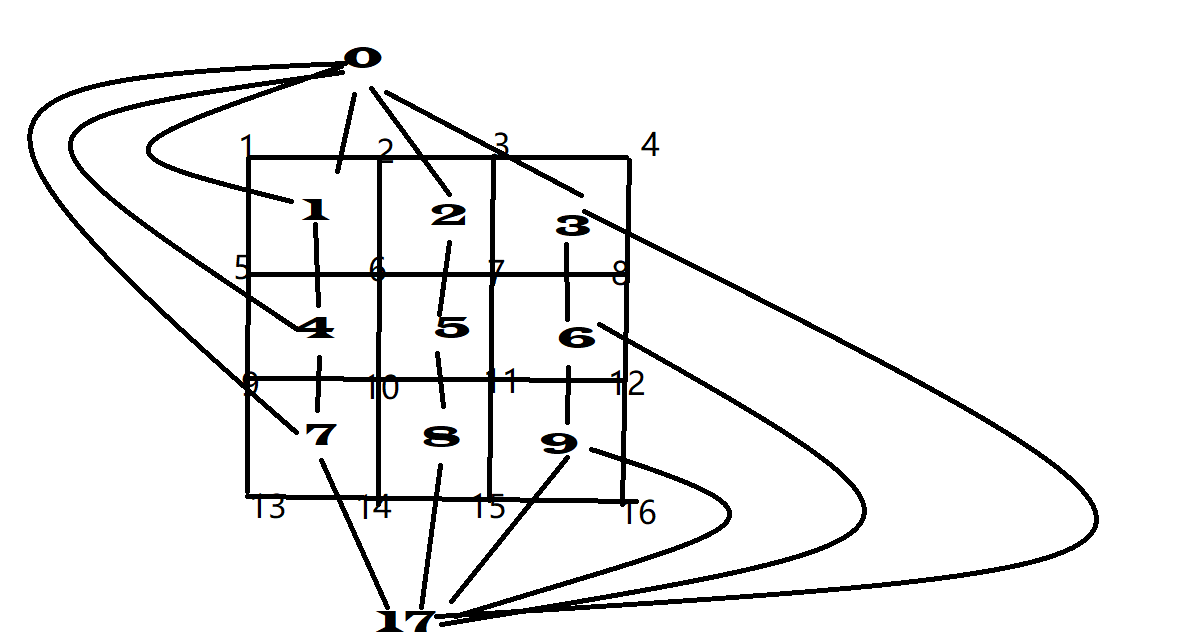
你可能会问：0 和 17 不是在一个面，为什么算两个节点？答：为了不构成环从而不方便处理。这一招在后续的对偶图最短路中很实用。
网格型平面图转对偶图
接下来说一下怎么把网格型平面图转对偶图。
对于无向图，按照上面的方法实现即可；对于有向图，对偶图中的方向只要边之间的相对方向是和原来相符的，你就可以自己定方向（比如下面的网格图，我们可以把以(1,1)-(n,n)对角线为分界线的右上面和左下面作为0和5，将原边顺时针旋转90°）
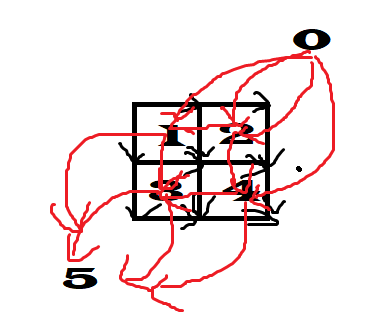
接下来说一下平面图转对偶图在平面（有向）图最小割中的应用。平面图按照经典算法求最小割的复杂度非常大的时候，转换为对偶图只需要求一次 O(nlogn) 的最短路即可解决。
具体来说，上图转换为平面图，将原来的边的边权对应赋给对偶图上的边权，那么原图的割对应对偶图上的一条从 s=0 到 t=5 的路径，从而只需要算出一条最短路即可。
另外，一般的平面图（不限于网格图）转对偶图的通法是“最小左转法”。对于每一条无向线段，拆成两个方向的有向线段各一条，一个封闭面由首尾顺次相接的有向线段构成的环围成，只需对每个点存下与它相连的线段有哪些，按atan2逆时针排个序，从其中一条开始逆时针求出一个面的组成线段，从一条到吓一跳的过程就是看箭头的点里这条线段顺时针旋转撞到的第一条线段，最后就可以给每条线段分配对应的两个面的编号了。
经典题：[NOI2020]海拔。（本题须注意最小割可以蜿蜒，所以所有的边都是有用的，合起来建一张图跑 Dij）
一般平面图转对偶图
《[WC2013]平面图》和《[HNOI2016]矿区》中的平面图并不是网格图，使用“最小左转法”转对偶图。
- 把每条无向线段拆成两条有向线段，定义一个面为一组逆时针的闭合有向线段圈围成的图形
- 将每条有向线段储存在箭尾处的点的 vector 中，把每个 vector 逆时针极角排序，预处理出每条有向线段在对应 vector 中的位置
- 从一条有向线段出发，对于当前的有向线段 \((s,t)\)，在 \(t\) 的 vector 中定位到 \((t,s)\)，它的上一条线段就是 \((s,t)\) 的下一条边，如此找出一个面，并记录每条有向线段属于哪个面
- 对每个面使用叉乘法计算面积，面积为负的一个面是无界面
