概率 dp 学习笔记
期望/概率 dp 是一类比较难推导的 dp,主要就难在思维。
概率 dp 的一个要点是:需要从终状态到始状态倒序推导,不然会 WA,原因见此。
Part 6.5 概率与期望
修改自——StudyingFather's Blog
P5104 红包发红包
P1850 换教室
P4550 收集邮票
P3830 [SHOI2012]随机树
P4564 [CTSC2018]假面
P2473 [SCOI2008]奖励关
P2221 [HAOI2012]高速公路
P3239 [HNOI2015]亚瑟王
P3750 [六省联考2017]分手是祝愿
P4284 [SHOI2014]概率充电器
P5249 [LnOI2019]加特林轮盘赌
P2081 [NOI2012]迷失游乐园
P3343 [ZJOI2015]地震后的幻想乡
P3600 随机数生成器
P5326 [ZJOI2019]开关
【例1】收集邮票
通过本题积累到了 dp 的推式子其实是可以最开始 \(f[i]=pf[i]+qf[X]+...\) 的,而最后通过恒等变换得出 \(f[i]\) 的递推式。
设 \(f[i]\) 表示当前取到了 \(i\) 种邮票,取掉剩下 \(n-i\) 号邮票的期望次数。
下一次取邮票时,有 \(\frac in\) 的概率取到已取的,贡献为 \(\frac inf[i]\);有 \(\frac{n-i}n\) 的概率取到未取的,贡献为 \(\frac{n-i}nf[i+1]\)。
设 \(g[i]\) 表示当前取到了 \(i\) 种邮票,取掉剩下 \(n-i\) 号邮票的期望价格。
下一次取邮票时,有 \(\frac in\) 的概率取到已取的,贡献为 \(\frac in(g[i]+f[i]+1)\);有 \(\frac{n-i}n\) 的概率取到未取的,贡献为 \(\frac{n-i}n(g[i+1]+f[i+1]+1)\)。
注云:也就是说先取“剩下的”再取“已取的”。
那么答案就是 \(g[0]\)。
Q:为什么答案不是 \(\frac{f[0](f[0]+1)}2\)?
A:实际情况中取的次数不等的两个方案是不能通过上述方式统一计算的,因此不能想当然。
【例2】OSU!
将形如 \(val(S)^k\) 的价值拆项是常见思路,更重要的是怎么利用。
易错:到底维护的是什么?对于 \(val^1,val^2\) 维护的是后缀的期望长度,对于 \(val^3\) 维护的是增量!
当一个1的连续段往右扩展一位时,由于 \((x+1)^3=x^3+3x^2+3x+1\),所以维护 \(f_1[i],f_2[i]\) 表示以 \(i\) 结尾的前缀,它期望的【1的连续后缀长度的 \(1,2\) 次方】是多少。维护 \(\delta[i]\) 表示以 \(i\) 结尾的后缀期望增加了多少,则
【例3】[LnOI2019]加特林轮盘赌
首先看到这种局面之间的变化的一定是要递推(DP)解决。
从题中抽象关键词——“人数”“\(k\) 幸存”——先设出状态 \(f[i][j]\) 表示 \(i\) 个人轮盘赌、第 \(j\) 个人唯一幸存的概率。要转移就要分类讨论:当 \(\bm{i\ge j\ge 2}\) 时,考虑讨论第一个人是否枪毙(在这里,我们把手枪指向的人称作第一人,按照循环顺序依次编号为 \(1\sim i\)),推出 \(f[i][j]=P_0f[i-1][j-1]+(1-P_0)f[i][j-1]\) 这个转移方程式(解释:第一项为第一人被枪毙,那么现在人数 \(i-1\)、\(j\) 的编号变为 \(j-1\);否则,手枪指向原来的第 2 人,从这个位置重新编号后 \(j\) 的编号是 \(j-1\))。
审视转移条件,我们的前提是 \(\bm{i\ge j\ge 2}\),也即我们并不知道 \(f[i][1]\)。从而一切的递推都无从说起。究其本质,我们有 \(i-1\) 个转移方程,有 \(f[i][1],f[i][2],\dots,f[i][i]\) 这 \(i\) 个变量,还差一个一次方程才能够解出每个变量,根据概率的性质,有:当 \(P_0>0\) 时,\(\sum_{j=1}^i f[i][j]=1\)。从而:以 \(\bm{f[i][1]}\) 为主元表示 \(\bm{f[i][2\sim i]}\),并根据最后一个方程解出答案。这是 dp 的一个常见方法。
【例4】CF908D New Year and Arbitrary Arrangement
(本来状态和转移都列对了,最后的类似等比数列求和的式子也写出来了,离正解不远了,但是 dp 的边界上的小 trick 没有 figure out 导致被搞蒙了,有点儿可惜……)
根据抽象关键词的方法,不难发现“子序列个数”应成为关键词,而考察 ab 子序列的形成方式,可以知道 a 的数量会在单个 b 的接入后造成巨变,所以“当前 a 的个数”也是一个备选关键词。
容易发现,虽然最后一步会有无穷 a、ab 子序列个数无穷多的情况,但是倒数第 2 步的 a 的数量一定是 ≤ K 的(这里“一步”代指一个 aa..ab(0个或多个a) 的产生)。因而设出 \(f[i][j]\) 表示 \(i\) 个 a,\(j\) 个 ab 子序列的局面的到达概率。有转移式 \(\forall j<K,\)
对于 达到结束状态 的局面,我们将 转移到它的局面 分为 2 类:(1)a 的数量不足 K(2)a 的数量至少 K。
对于(1),我们只要在转移的过程中将第二排的转移时 \(j+i\ge K\) 的情况特殊处理——ans+=(j+i)*f[i][j]*pb——就能完全统计这种情况了;对于(2),在 \(i=K\) 时,我们看最后是 \(K+几\) 个 a,那么答案肯定是 \(f[i][j]\cdot p_b\sum_{i=0}^{\infin}(ip_a^i)\),咱们使用一些手段化简可以得出它的得数是 \(f[i][j]\cdot {p_a+p_b(i+j)\over p_b}\)。
那么现在就来谈一谈文首提到的 dp 边界问题——我们的 dp 边界到底是什么呢?
事实上,你要观察到一个小性质,就是最开始的时候你不管随到多少个 b 放在最前面,都不会对最后 ab 子序列的数目有任何影响,也不会影响后面的 a 的转移什么的,所以你完全可以钦定第一个放的是 a,即 f[1][0]=1。这样可以彻底避免一个非常非常 confusing 的问题,就是 \(i=0\) 的时候的第二种转移方程怎么转移。
此题解。
#include <bits/stdc++.h>
using namespace std;
const int N=1005,mod=1e9+7;
int K,pa,pb,ans,f[N][N];
int qp(int a,int b){
int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
return c;
}
int main(){
cin>>K>>pa>>pb;
int tmp=qp(pa+pb,mod-2);
pa=1ll*pa*tmp%mod,pb=1ll*pb*tmp%mod;
int _pb=qp(pb,mod-2);
f[1][0]=1;
for(int i=1;i<=K;i++)for(int j=0;j<K;j++){
(f[i+1][j]+=f[i][j]*1ll*pa%mod)%=mod;
if(i==K)(ans+=1ll*f[i][j]%mod*_pb%mod*((pa+1ll*pb*(i+j)%mod)%mod)%mod)%=mod;
else if(j+i<K)(f[i][j+i]+=f[i][j]*1ll*pb%mod)%=mod;
else (ans+=1ll*(j+i)*f[i][j]%mod*pb%mod)%=mod;
}
cout<<ans;
}
【例5】[HNOI2013]游走
最初的思路是 dp 最小得分,把每条边的编号当未知数 x[i],dp 到 n 点的时候各 x[i] 前面的系数作为分配编号的依据。然而容易发现非常不可行,特别是起点附近的转移难以写出。其根本原因,是因为我们的 dp 依赖于时间的推移。
是否存在不依赖于时间推移的整体视角的做法呢?我们发现其实从一开始我们实际关心的就是边的经过次数,所以不如就 dp 经过次数。但是你会发现边的描述很麻烦,各种细节的处理亦相对繁琐,由于边的经过次数完全取决于两端点的经过次数,即设两端点 \(u,v\) 的经过次数为 \(f_u,f_v\),则边的经过次数必为 \(\frac{f_u}{d_u}+\frac{f_v}{d_v}\)(\(d_u\) 为 \(u\) 的度数)。
因此设 \(f_u\) 为点 \(u\) 的期望经过次数,不难得出转移方程 \(\forall 2\le u< n,f_u=\sum_{(u,v)\in E,v\ne n}\frac{f_v}{d_v}\),\(f_1=1+\sum_{(1,v)\in E,v\ne n}\frac{f_v}{d_v}\);我们不予考虑 \(f_n\),因为一到 \(n\) 点就结束了。虽然我们不清楚 dp 的边界在哪里,但是我们有 \(n-1\) 个方程 \(n-1\) 个未知数就可采用高斯消元解出各个 \(f_u\)。将期望经过次数小的边分配大编号,就做完了。
时间复杂度 \(O(m+n^3)\)。
【例6】[ZJOI2015]地震后的幻想乡
考察 Kruskal 生成树的过程,默认按照边权从小到大加边,只要图不连通我们就继续加边,直到加入一条边 \(i\) 后图连通了,然后我们取所有我们加入的边(共 \(i\) 条)的最大的那个,也即 \(m\) 条边中期望第 \(i\) 小,\(i\over m+1\)。
考虑将 \(i\over m+1\) 拆给每一条边,看做它们做贡献,每枚举一条边贡献 \(1\over m+1\)。那么我们枚举到第 \(i\) 条边的充要条件是加入 \(i-1\) 条边时图还不联通。也就是说,如果 \(p_{i-1}\) 表示加入 \(i-1\in [0,m-1]\) 条边后图不连通的概率,那么有 \(p_{i-1}\) 的概率第 \(i\) 条边产生 \(1\over m+1\) 的贡献。而 \(p_{i-1}=\frac{a_{i-1}}{m\choose i-1}\),其中 \(a_{i-1}\) 为加入 \(i-1\) 条边后不连通的方案数,这是我们接下来需要求解的。
抽象关键词——“加边条数”“是否连通”。设 \(f_{S,i}\) 表示加入 \(i\) 条边后点集 \(S\) 不连通的方案数,那么根据图连通性 dp 的套路,固定一个 \(x\in S\),并枚举 \(x\) 所属的连通块进行转移——\(x\in T\subset S\) 且 \(T\) 应连通,那么为了满足后者的限制,对称地设出 \(g_{S,i}\) 表示加入 \(i\) 条边后点集 \(S\) 连通的方案数,于是 \(S-T\) 中的部分可以随便选,且钦定 \(T\) 与 \(S-T\) 之间不存在连边,这样 \(f_{S,i}=\sum_T\sum_j g_{T,j}{|E_{S-T}|\choose i-j}\) 的转移方程便得出了;\(g_{S,i}={|E_S|\choose i}-f_{S,i}\)。
将 \(a_i=f_{2^n-1,i}\) 代入最初的式子即得答案。
#include <bits/stdc++.h>
using namespace std;
int n,m,u[50],v[50],cnt[1030];
double C[50][50],f[1030][50],g[1030][50];
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++)cin>>u[i]>>v[i];
for(int msk=1;msk<(1<<n);msk++)
for(int i=1;i<=m;i++)if((msk>>(u[i]-1)&1)&&(msk>>(v[i]-1)&1))
cnt[msk]++;
C[0][0]=1;
for(int i=1;i<=m;C[i][0]=1,i++)
for(int j=1;j<=i;j++)C[i][j]=C[i-1][j]+C[i-1][j-1];
for(int s=1;s<(1<<n);s++){
int lb=s&-s;
if(__builtin_popcount(s)==1)g[s][0]=1;
else f[s][0]=1;
for(int i=1;i<=cnt[s];i++){
for(int t=(s-1)&s;t;t=(t-1)&s)if(t&lb)
for(int j=0;j<=min(i,cnt[t]);j++)
f[s][i]+=g[t][j]*C[cnt[s-t]][i-j];
g[s][i]=C[cnt[s]][i]-f[s][i];
}
}
double ans=0;
for(int i=0;i<m;i++)ans+=f[(1<<n)-1][i]/C[m][i];
ans/=m+1;
printf("%.6f\n",ans);
}
【练1】[PKUSC2018]最大前缀和
从部分分出发考察性质,“满足 a 中至多一个负数”怎么做?好吧这个很简单,但是它提醒我们从负数的 POV 考虑。不难发现,最大前缀和的结束为止一定是某个负数之前,而这个位置 \(i\) 作为最大前缀和的充要条件就是 \(\forall j\in [1,i]\),前缀和 \(j\) 都 \(\le\) 前缀和 \(i\),\(forall j\in (i,n]\),前缀和 \(j\) 都 \(<\) 前缀和 \(i\)。不难发现,就是 \([1,i]\) 的每一个后缀和 \(\ge 0\),\([i+1,n]\) 的每一个前缀和 \(<0\)。
这就是分成两部分,一部分满足条件一,另一部分满足条件二的意思啊!显然的状压 DP。设 \(f(s),g(s)\) 分别表示选出并排列 \(s\),使得满足前者和后者的方案数。
最后的统计答案,发现有点小小问题,就是如果第一个数是负数,就会统计不到,所以我们令 \(f(0)=g(0)=1\),然后枚举第一个数,这样实在不行可以选空集。
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,ans,a[25],f[1<<20],g[1<<20];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=0;i<n;i++)if(a[i+1]>=0)f[1<<i]=1;else g[1<<i]=1;
for(int s=0;s<(1<<n);s++){
if(s==(s&-s))continue;
int sum=0;
for(int i=0;i<n;i++)if(s>>i&1){
sum+=a[i+1];
add(f[s],f[s^(1<<i)]);
}
if(sum<0)f[s]=0;
}
for(int s=0;s<(1<<n);s++){
if(s==(s&-s))continue;
int sum=0;
for(int i=0;i<n;i++)if(s>>i&1){
sum+=a[i+1];
add(g[s],g[s^(1<<i)]);
}
if(sum>=0)g[s]=0;
}
f[0]=g[0]=1;
for(int i=1;i<=n;i++){
int U=((1<<n)-1)^(1<<(i-1));
for(int s=0;s<(1<<n);s++)if((s&U)==s){
int sum=a[i];
for(int j=0;j<n;j++)if(s>>j&1)sum+=a[j+1];
sum=(sum%mod+mod)%mod;
add(ans,1ll*f[s]*g[U^s]%mod*sum%mod);
}
}
cout<<ans;
}
【练2】[PKUWC2018]随机算法
【套路】独立集 DP 时,重点观察独立集内节点的邻居集合,每加入一个点到独立集,就把它和它的邻居一起加入状态,而独立集自身通过大小刻画即可。
设 \(f(i,s)\) 表示独立集大小为 \(i\),独立集中点连同其所有邻居占据集合 \(s\),的方案数。考虑下一个 加入独立集 的点,它应该和 \(s\) 无交集,这种情况下可以转移到 f(i+1,s|(1<<k-1)|adj[k]),转移系数是 \(A_{n-1-|s|}^{|s\cup adj_k|-|s|}\)。
算出最大独立集大小 \(mx\),答案就是 \(f(mx,U)\)。
【练3】[PKUWC2018]随机游走
什么是 Min-Max 容斥?
\(\min_{i\in S} a_i=\sum_{T\subseteq S}(-1)^{\color{red}{|T|+1}}\max_{i\in T}a_i\)
\(\max_{i\in S} a_i=\sum_{T\subseteq S}(-1)^{\color{red}{|T|+1}}\min_{i\in T}a_i\)
在本题中,\(a_i\) 就是集合中各点的到达时间,最晚到达时间是所求,但最早到达时间更容易计算。
为什么最早到达时间更容易 DP 呢?这是因为如果设 \(f(i,s)\) 表示从 \(i\) 去 \(s\) 中所有点至少一次的期望步数,就不知道边界在哪,但如果设成去到 \(s\) 中最近一点的期望步数,边界就是 \(s\) 中点自身的 \(f(i)=0\)。(当然我也不确定是不是那样一定不可做,因为貌似也没错,但是容斥后做肯定可做)

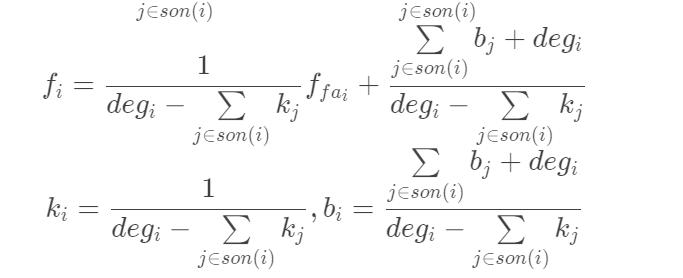
考虑到根节点(起点 \(x\))不能从“父亲”转移,所以转移式没有 "fa" 一项,因此 \(f_{rt}=b_{rt}\)。Min-Max 部分用高维前缀和加速。
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,q,rt,k[20],b[20],g[1<<18];
vector<int>G[20];
inline void add(int &x,int y){(x+=y)>=mod&&(x-=mod);}
inline int qp(int a,int b){int c=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;return c;}
void dfs(int x,int p,int s){
int sk=0,sb=0;
for(int y:G[x])if(y^p){
dfs(y,x,s);
add(sk,k[y]),add(sb,b[y]);
}
if(s>>(x-1)&1)k[x]=b[x]=0;
else k[x]=qp(((int)G[x].size()+mod-sk)%mod,mod-2),b[x]=1ll*(sb+G[x].size())*k[x]%mod;
}
int main(){
cin>>n>>q>>rt;
for(int i=1,u,v;i<n;i++)
cin>>u>>v,G[u].emplace_back(v),G[v].emplace_back(u);
for(int s=1;s<(1<<n);s++){
dfs(rt,0,s);
g[s]=b[rt]*(__builtin_popcount(s)&1?1ll:mod-1ll)%mod;
}
for(int w=1;w<(1<<n);w<<=1)
for(int i=0;i<(1<<n);i+=w<<1)
for(int j=0;j<w;j++)
add(g[i+j+w],g[i+j]);
while(q--){
int K,tmp,s=0;
cin>>K;
while(K--)cin>>tmp,s|=1<<(tmp-1);
cout<<g[s]<<'\n';
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号