[ZJOI2017]仙人掌

原题链接
AC记录

Part 0 基本思路

1. 如果给出的图一开始就不是仙人掌，则输出 0，否则：
2. 如果一条边处在某个环中，则新加的边一定不会跨过它。
3. 题目转化为求：把树上的边划为若干条路径的方案数。其中“路径”指由若干连续的边构成的链。
4. 考虑树形 dp。

Part 1 判定仙人掌

判定无向连通图是否是仙人掌可以采用 dfs+树上差分的办法。具体来说，对图进行 dfs，那么会形成一个 dfs 树，对于当前遍历到的点 \(x\)，如果存在一条“返祖边”\((x,y)\)，则可以让 \(x\) 的差分值 \(+1\)，\(y\) 的差分值 \(-1\)，表示 \(x\) 到 \(y\) 的树上路径中的边被一个环包含；一个点的差分值表示连接它与它父节点的边被覆盖的差分次数。再进行一轮 dfs 计算树上前缀和。图是仙人掌等价于最后每个点的值均 \(\le 1\)。

Part 2 求强联通分量

下面阐述为什么需要求强联通分量。

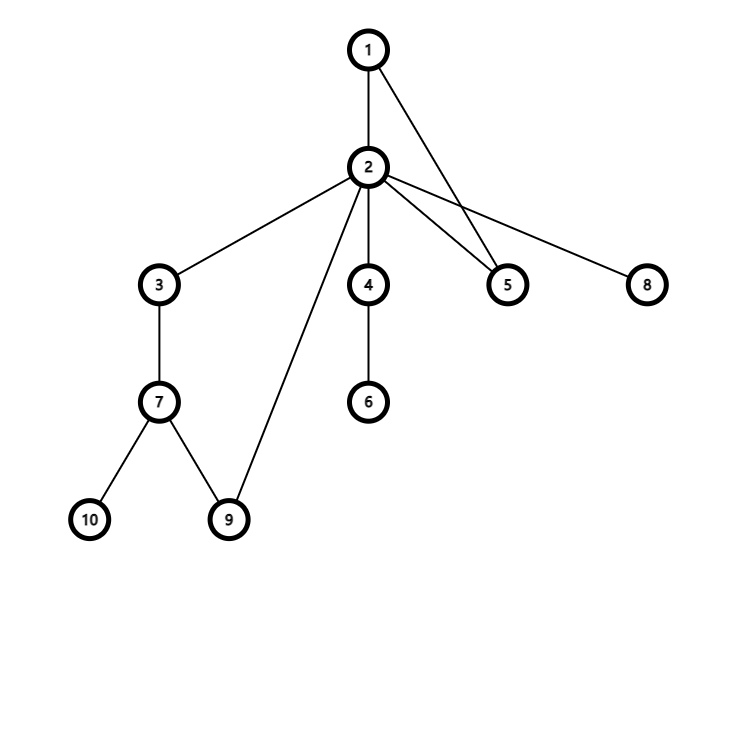
考虑上图。新加的边一定不会跨过包含两个及以上点的强联通分量的任一条边【*】。而 \(\{3,7,9,1,2,5\},\{10\},\{4\},\{6\},\{8\}\) 为本图中的强联通分量。【*】该如何翻译成程序可以执行的语言，是我们应该思考的问题。
目前来看，这个问题尚不好解决，我们先看下面的思路。

Part 3 树形 dp

让我们先来考虑最为理想的情况：题图为一棵树。
根据 Part 0.3 的说法，我们可以设 \(f_{i}\) 表示 \(i\) 的子树内部的划分方案数。\(\prod_{j\in son(i)}f_j\) 是容易想到的。现在就需要把 \(i\) 的儿子连起来，那么需要乘以 \(h_{|son(i)|}\)，\(h_i\) 表示的是

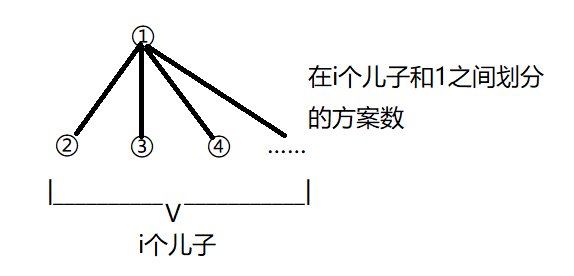
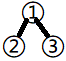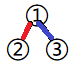就比如说就有和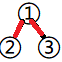两种划分方式。容易得出递推式 \(h_i=h_{i-1}+(i-1)\cdot h_{i-2}\)。解释：现在又多了一个儿子，那么这个儿子可以不跨根或者跨根，不跨根就是 \(h_{i-1}\)，跨根就还剩独立的 \(i-2\) 个儿子，就是 \(h_{i-2}\)，而它选择跟哪个儿子又有 \((i-1)\) 种方案，总的就是 \((i-1)\cdot h_{i-2}\)。
那答案是不是就是 \(\prod_{j\in son(i)}f_j\cdot h_{|son(i)|}\) 呢？不是，因为无法实现跨儿子的路径。这时候我们就需要更改 \(f_i\) 的定义了。改成表示 \(i\) 的子树中跨 \(i\) 和不跨 \(i\) 的方案数之和。也就是可以在 \(i\) 这里断开也可以不断开，都考虑到了。转移方程也有变化，就是 \(\prod_{j\in son(i)}f_j\cdot h_{|son(i)|+1}\)。\(+1\) 的原因是还需要考虑跟不跟父亲相连。另外整棵树的根 \(1\) 号点是个例外，因为它没有父亲，所以它的转移就是不需要那个 \(+1\)。

补充：为什么能够转化为 Part 0.3的说法？你可以想象节点是钉子，我们所加的新边是橡皮筋，每加一条边就让橡皮筋去贴到它的端点间树上路径上所有钉子上绷着。那么相邻两点间不能有多段橡皮筋。而如果相邻两点间没有橡皮筋，你可以想象其实有一条橡皮筋连着它们。这样一棵树就可以被看成多条路径拼成的。

回到 Part 2

现在可能有一些思路了，那么【*】怎么落实呢？我们发现如果 \(i\) 和父节点属于同一强连通分量【*'】，就不需要那个 \(+1\)。另外还会影响 \(|son(i)|\)，因为有一些儿子是无论如何也不会参与划分的。这样的儿子就是 【*'】为假的节点。
那么回到上面的图，为什么 \(6,8\)、\(4,8\) 能产生答案，其实回答很显然了，\(f_6=f_8=1\)，\(f_4=2\)，\(f_2=f_3f_4f_5f_8h_{2+0}=4\)，答案就是 \(4\) 了。

附注

为了后人调试之方便，下贡献一组样例。
sample.in:

6
3 2
1 2
1 3

5 4
1 2
2 3
2 4
1 5

10 10
8 4
8 7
8 5
8 6
1 9
6 10
5 2
4 1
6 3
8 2

10 11
4 6
2 3
7 10
9 7
4 2
2 5
2 1
1 5
7 3
2 9
2 8

6 7
2 3
1 3
4 5
5 6
4 6
1 4
2 5

10 11
2 10
4 7
10 9
3 8
3 6
3 7
1 7
1 5
1 2
4 3
2 4

sample.out:

2
8
64
4
0
0