DP 优化
Part 1 最长上升子序列
优先队列优化最长上升子序列。每次将求完的 \(f_i\) 丢进 priority_queue，求最大值时取堆顶。
复杂度 \(O(n^2)\to O(n\log n)\)
Part 2 线段树优化 DP
写出常规 DP 转移方程式，区间修改、查询如果可以用线段树维护就可将 \(O(n)\to O(\log n)\)。
【例 1】[TJOI2011]书架
已知长为 \(n\) 的数组 \(a\)、整数 \(m\)，将 \(a\) 分为若干连续段，要求每段和 \(\le m\)，求每段最大值之和的最小值。
设 \(f_i\) 表示前缀 \(a_{1...i}\) 的答案，
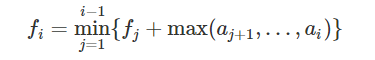
发现没有办法用线段树维护一个既含 \(\max\) 又含 \(\min\) 的东西，但是它可以维护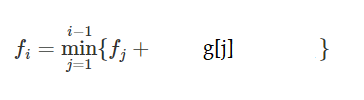
,其中 \(g_j\) 为一个和 \(f_j\) 地位相等的量；它可以支持对 \(f_j,g_j\) 的实时修改和对 \(f_j,g_j,f_j+g_j\) 的实时查询。
观察到 \(a_i\) 的添加只会对 \(j\in[pre_i+1,i]\) 的 \(\max(a_{j+1},...,a_i)(1)\) 产生影响，其中 \(pre_{i}\) 表示 \(i\) 前面最近的大于等于 \(a_i\) 的数的位置，因此可以令 \(g_j\) 表示式子 \((1)\) 的值，而对 \(g_{pre_i+1}...g_i\) 区间修改为 \(a_i\) 即可。
求 \(f_i\) 时需要查询 \(q\sim i\) 的 \(f+g\) 的和即可，求完之后在线段树中单点更新 \(f_i\)。
下面代码实现中维护的 \(fm\) 实际上是 \(f_{i-1}+g_i\)，$f% 实际上是 \(f_{i-1}\)。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
#define int long long
int n,m,top,a[N],s[N],stk[N],pre[N],f[N];
struct segmt {
int f,fm,tag;
}t[N<<2];
void pushup(int k){
t[k].f=min(t[k<<1].f,t[k<<1|1].f);
t[k].fm=min(t[k<<1].fm,t[k<<1|1].fm);
}
void pushdown(int k){ //change max
if(!t[k].tag)return;
t[k<<1].tag=t[k<<1|1].tag=t[k].tag;
t[k<<1].fm=max(t[k<<1].fm,t[k<<1].f+t[k].tag);
t[k<<1|1].fm=max(t[k<<1|1].fm,t[k<<1|1].f+t[k].tag);
t[k].tag=0;
}
void build(int l,int r,int k){
if(l==1&&l==r){t[k].tag=0,t[k].f=t[k].fm=0;return;}
if(l==r){t[k].tag=0,t[k].f=t[k].fm=1e9;return;}
int mid=l+r>>1;
build(l,mid,k<<1),build(mid+1,r,k<<1|1);
pushup(k);
}
void chgmx(int L,int R,int v,int l,int r,int k){
if(L<=l&&r<=R){
t[k].tag=v;
t[k].fm=v+t[k].f;
return;
}
pushdown(k);
int mid=l+r>>1;
if(L<=mid)chgmx(L,R,v,l,mid,k<<1);
if(R>mid)chgmx(L,R,v,mid+1,r,k<<1|1);
pushup(k);
}
void chgf(int p,int v,int l,int r,int k){
if(l==r){t[k].fm-=t[k].f,t[k].fm+=v,t[k].f=v;return;}
pushdown(k);
int mid=l+r>>1;
if(p<=mid)chgf(p,v,l,mid,k<<1);
else chgf(p,v,mid+1,r,k<<1|1);
pushup(k);
}
int ask(int L,int R,int l,int r,int k){
if(L<=l&&r<=R)return t[k].fm;
pushdown(k);
int mid=l+r>>1,ans=1e9;
if(L<=mid)ans=min(ans,ask(L,R,l,mid,k<<1));
if(R>mid)ans=min(ans,ask(L,R,mid+1,r,k<<1|1));
return ans;
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
s[i]=s[i-1]+a[i];
while(top&&a[stk[top]]<a[i])top--;
if(top)pre[i]=stk[top];
stk[++top]=i;
}
build(1,n,1);
for(int i=1;i<=n;i++){
int q=lower_bound(s,s+n+1,s[i]-m)-s+1;//printf("(q|%d)",q);
chgmx(pre[i]+1,i,a[i],1,n,1);
f[i]=ask(q,i,1,n,1);
if(i<n)chgf(i+1,f[i],1,n,1);
//cout<<f[i]<<' ';
}
cout<<f[n];
}
Part 2' 树套树优化 dp
序列
题目问的是子序列，就用子序列的视角。问自己：“一个合法子序列满足什么条件（性质）？”
Part 3 前缀和优化(后缀和优化)
由于 \(x\) 只出现了一次，而且每次都是查 \(j+1\sim m+1\) 这个后缀，因此通过结合律可以知道
#include <bits/stdc++.h>
using namespace std;
const int N=305;
int n,m,mod,f[N][N],t[N][N],C[N][N];
int main(){
cin>>n>>m>>mod;
C[0][0]=1;
for(int i=1;i<=n;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
for(int i=1;i<=m+1;i++)f[0][i]=1;for(int i=m;i;i--)t[0][i]=t[0][i+1]+f[0][i+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
for(int k=0;k<i;k++)
(f[i][j]+=1ll*t[k][j]*f[i-1-k][j]%mod*C[i-1][k]%mod)%=mod;
for(int j=m;j;j--)t[i][j]=(t[i][j+1]+f[i][j+1])%mod;
}
cout<<f[n][1];
}
Part 4 斜率优化
- https://www.cnblogs.com/impyl/p/15876495.html
- [SDOI2016]征途
Part 5 决策单调性优化
则主要求 \(f_i=\max_{j<i}\{h_j+\sqrt{i-j}\}\)，而 \(j>i\) 是同理的。
所求式可以看成是对于每一个 \(j\)，有一个函数 \(f_j(i)=h_j+\sqrt{i-j}(i\ge j)\)
在同一张纸上画出各函数图像↓（借用了他人博客图片）
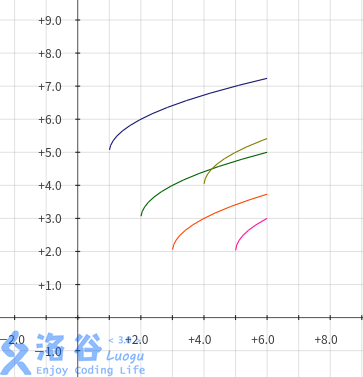
我们知道 \(\sqrt x\) 函数的增长速率单调减慢，所以每个时刻的值最大（最考上）的函数所属的 \(j\) 一定是单调不降的。
我们发现了决策单调性。
如何使用决策单调性
用一个“单调队列”存储若干三元组 \((j,l,r)\)，表示目前，\([l,r]\) 的最优决策为 \(j\)，所有的 \([l,r]\) 并起来应该是 \([i,n]\) 这个区间。
- 取出队头 \((j,l,r)\)，若 \(r<i\)，弹出。
- 将队头的 \(l\) 设为 \(i\)
- 计算 \(f[i]\)
- 取出队尾 \((j,l,r)\)，若对于 \(f_l\)，\(j\) 比 \(i\) 劣，则结合单调性可知 \([l,r]\) 都废除，令 \(pos=l\)，重复此步骤（直到队空or不满足条件）
- 取出队尾 \((j,l,r)\)，若对于 \(f_r\)，\(j\) 比 \(i\) 劣，则在 \([l,r]\) 上二分一个最小的 \(mid\) 使得对于 \(f_mid\)，\(j\) 比 \(i\) 劣，令 \(pos=mid\)
- 将 \((i,pos,n)\) 入队尾
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,l,r,h[N];
double f[N],g[N];
struct J {
int x,l,r;
}q[N];
void solve(int h[],double f[]){
l=1,r=0;q[++r]={1,1,n};
for(int i=2;i<=n;i++){
while(l<=r&&q[l].r<i)l++;
q[l].l=i;
f[i]=h[q[l].x]+sqrt(i-q[l].x);
int pos=n+1;
while(l<=r&&h[q[r].x]+sqrt(q[r].l-q[r].x)<h[i]+sqrt(q[r].l-i))pos=q[r].l,r--;
if(l<=r&&h[q[r].x]+sqrt(q[r].r-q[r].x)<h[i]+sqrt(q[r].r-i)){
int L=q[r].l-1,R=q[r].r+1,mid;
while(L<R-1){
mid=L+R>>1;
if(h[q[r].x]+sqrt(mid-q[r].x)<h[i]+sqrt(mid-i))R=mid;
else L=mid;
}
pos=R;
}
if(pos<=n)q[r].r=pos-1,q[++r]={i,pos,n};
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>h[i];
solve(h,f);
reverse(h+1,h+n+1);
solve(h,g);
reverse(h+1,h+n+1);
reverse(g+1,g+n+1);
for(int i=1;i<=n;i++)cout<<max(0,(int)(ceil(max(f[i],g[i]))-h[i]))<<'\n';
}
Part 6 随机化优化 dp
- 平面随机游走：\(O(n^2)\to O({\sqrt n}^2)=O(n)\)
THUPC2021混乱邪恶
暴力的bool f[i][x][y][l][g]的dp是\(O(n^3p^2)\)的，bool 数组用bitset替代、整体位运算来转移可以 \(\div \omega\)，然而还是过不了；考虑平面随机游走，把每个步的6个方向random_shuffle，把n步random_shuffle，再去遍历，就相当于随机游走了，除非极端数据（题目中没有），都可以保证最远距离原点在 \(\sqrt n\) 级别的远处，这样就缩掉一个O(n)了，总复杂度\(O(n^2p^2/\omega)\).
#include <bits/stdc++.h>
using namespace std;
const int N=105;
int n,p,L0,G0,b[N][7][2][2],d[7][2]={{0,0},{0,1},{-1,0},{-1,-1},{0,-1},{1,0},{1,1}};
bitset<N>f[2][32][32][N],P;
int main(){
cin>>n>>p;
for(int i=0;i<p;i++)P[i]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=6;j++)for(int k=0;k<=1;k++)cin>>b[i][j][1][k],b[i][j][0][k]=d[j][k];
for(int j=2;j<=6;j++)swap(b[i][j],b[i][rand()%j+1]);
}
random_shuffle(b+1,b+n+1);
cin>>L0>>G0;
const int qw=30;
f[1][15][15][0][0]=1;
for(int i=1;i<=n;i++){
for(int x=0;x<=qw;x++)
for(int y=0;y<=qw;y++)
for(int l=0;l<p;l++){
if(f[i&1][x][y][l].none())continue;
for(int j=1;j<=6;j++){
int x_=x+b[i][j][0][0],y_=y+b[i][j][0][1];
int l_=(l+b[i][j][1][0])%p;
if(x_<0||y_<0)continue;
f[~i&1][x_][y_][l_]|=P&(f[i&1][x][y][l]<<b[i][j][1][1])|f[i&1][x][y][l]>>(p-b[i][j][1][1]);
}
}
for(int x=0;x<=qw;x++)
for(int y=0;y<=qw;y++)
for(int l=0;l<p;l++){
f[i&1][x][y][l]=0;
}
}
puts(f[~n&1][15][15][L0][G0]?"Chaotic Evil":"Not a true problem setter");
}
Part 7 路径计数模型优化 dp
遇到利用常规方法难以优化的 dp，可考虑转化为路径计数模型：eg1.f[i][j]=f[i-1][j]+f[i][j-1] eg2.f[i][j]=f[i-1][1]+f[i-1][2]+...+f[i-1][j]（如果做k次前缀和，则f[k+1][i]转化为i个球分到k个盒子里的问题，可以为空）
