11.1 模拟赛:订正
最近几次模拟赛都比较难,一一爆零。要么是完全不知道怎么做,要么是因为对于一道自己认为很有思路的题一直调不出来。不过确实应该首先写好所有的暴力。
进入正题。http://47.92.197.167:5283/contest/115
Author:Kewth
T1 集合均值

等价于是随机生成 \(B\) 的排列,求所有前缀的“平均”(当然还要算开头的 \(0\))。那么
那么由于所有的排列方案我们都会算到,而 \(a_i\) 放在排列中每一个位置 \(x\) 的贡献为 \(g(x)\cdot a_i\cdot (|B|-1)!\),所以由分配律得答案为 \(\sum_{i=1}^{|B|}a_i\times\sum_{i=1}^{|B|} g(i)\times \dfrac{(|B|-1)!}{方案数}\)。
那么有多少种方案呢?显然是 \(|B|!\),因此最终答案为
其中 \(g(i)\) 可以由逆元线性推导出,因此复杂度为 \(O(n)\)。
备注:之前一直没有调出来就是因为算贡献的时候没有乘上 \((|B|-1)!\) !
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 5, M = 2e7 + 5, mod = 998244353;
int read() {
char ch = getchar();
int x = 0, f = 1;
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-')
f = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
return x * f;
}
int n, m, sum, tot, a[N], jc[M], ijc[M], inv[M];
int qp(int a, int b) {
int c = 1;
for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1)
c = 1ll * c * a % mod;
return c;
}
int inver(int b) {
return qp(b, mod - 2);
}
int frac(int a, int b) { return qp(b, mod - 2) * a % mod; }
signed main() {
freopen("mos.in", "r", stdin);
freopen("mos.out", "w", stdout);
n = read(), m = read();
jc[0] = ijc[0] = inv[0] = 1;
for (int i = 1; i <= n; i++) a[i] = read(), tot = (tot + a[i]) % mod;
for (int i = 1; i <= n * m + 1; i++) jc[i] = 1ll * jc[i - 1] * i - 1ll * jc[i - 1] * i / mod * mod;
ijc[n * m + 1] = inver(jc[n * m + 1]);
for (int i = n * m; i; i--) ijc[i] = 1ll * ijc[i + 1] * (i + 1) - 1ll * ijc[i + 1] * (i + 1) / mod * mod;
for (int i = 1; i <= n * m + 1; i++) inv[i] = 1ll * ijc[i] * jc[i - 1] % mod;
int s = 0;
for (int i = n * m + 1; i > 1; i--) s = (inv[i] + s) % mod, sum = (sum + s) % mod;
cout << 1ll * m * tot % mod * sum % mod * inv[n * m] % mod;
}
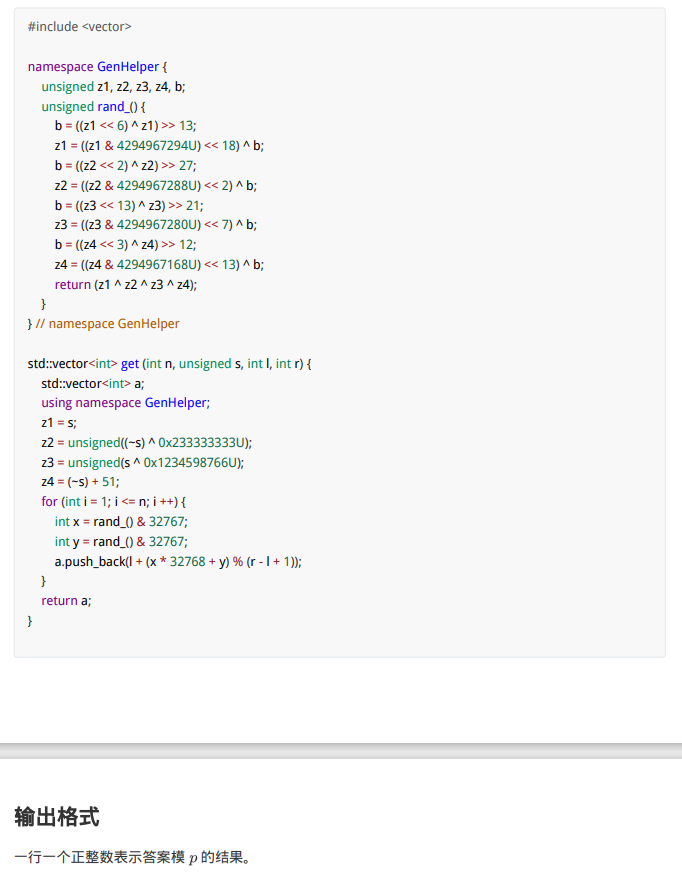
T3 技术情报局

区间?最大值?笛卡尔树! 这就是本题核心。
参见 笛卡尔树 O(n) 建树方法 建立笛卡尔树(大根)。观察到如果我们记录左右子树所代表的区间的“左端点连乘和”&“右端点连乘和”(为了方便叙述而定义的名词,“左端点连乘和”表示 \(fl([l,r])=\sum_{i=l}^r\left(\prod_{j=l}^ia_i\right)\))设树中 \(f(x)\) 表示 \(x\) 所代表区间的 \(\prod\),则可以 O(1) 地更新每一个根的 \(f,fl,fr\),具体见代码。
考虑对于一个根如何统计以它为最大值的区间答案,显然答案加上 \((fr(ls_x)+1)\cdot(fl(rs_x)+1)\cdot a_x^2\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e7 + 5;
int n, l, r, s, p, n_, k, top, ans, a[N], ls[N], rs[N], stk[N], f[N], fl[N], fr[N];
namespace GenHelper {
unsigned z1, z2, z3, z4, b;
unsigned rand_() {
b = ((z1 << 6) ^ z1) >> 13;
z1 = ((z1 & 4294967294U) << 18) ^ b;
b = ((z2 << 2) ^ z2) >> 27;
z2 = ((z2 & 4294967288U) << 2) ^ b;
b = ((z3 << 13) ^ z3) >> 21;
z3 = ((z3 & 4294967280U) << 7) ^ b;
b = ((z4 << 3) ^ z4) >> 12;
z4 = ((z4 & 4294967168U) << 13) ^ b;
return (z1 ^ z2 ^ z3 ^ z4);
}
} // namespace GenHelper
void get(int n, unsigned s, int l, int r) {
using namespace GenHelper;
z1 = s;
z2 = unsigned((~s) ^ 0x233333333U);
z3 = unsigned(s ^ 0x1234598766U);
z4 = (~s) + 51;
for (int i = 1; i <= n; i++) {
int x = rand_() & 32767;
int y = rand_() & 32767;
a[++n_] = (l + (x * 32768 + y) % (r - l + 1));
}
}
void dfs(int x) {
f[x] = a[x];
if (ls[x])
dfs(ls[x]), f[x] *= f[ls[x]], f[x] %= p;
if (rs[x])
dfs(rs[x]), f[x] *= f[rs[x]], f[x] %= p;
fl[x] = (fl[ls[x]] + (fl[rs[x]] + 1) * f[ls[x]] % p * a[x] % p) % p;
fr[x] = (fr[rs[x]] + (fr[ls[x]] + 1) * f[rs[x]] % p * a[x] % p) % p;
ans += (fr[ls[x]] + 1) * (fl[rs[x]] + 1) % p * a[x] % p * a[x] % p, ans %= p;
// printf("%d: %d %d %d\n",x,f[x],fl[x],fr[x]);
}
signed main() {
freopen("tio.in", "r", stdin);
freopen("tio.out", "w", stdout);
cin >> n >> s >> l >> r >> p;
get(n, s, l, r);
for (int i = 1; i <= n; i++) {
int k = top;
while (k && a[stk[k]] < a[i]) k--;
if (k)
rs[stk[k]] = i;
if (k < top)
ls[i] = stk[k + 1];
stk[++k] = i;
top = k;
}
int id = 0;
for (int i = 1; i <= n; i++)
if (a[id] < a[i])
id = i;
f[0] = 1;
dfs(id);
cout << ans;
}
对我来说这两题难度都不算简单,但在本场比赛中似乎是签到题……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号