luogu赛道修建
介绍
- 本篇文章是我写过的最详细易懂的一篇题解,同时也是我用 GitHub 写的第一篇题解。
- 这篇题解力求在分析过程方面帮助到更多的人,并且我个人认为比其他题解要容易理解许多。
- 如果你想要更佳的阅读体验,请点击此处。
分析阶段
要想让最小值最大,这类题目一般采用二分答案的方法。二分我们的最小赛道长,然后每次在树上构建长度大于等于二分到的值 \(mid\) 的赛道,看看是否可以构建出不小于 \(m\) 条赛道。
这一步不难想到,此题的难点在于如何去判断 \(mid\) 是否可以构建出合法条件的赛道,即如何在树上构建合法赛道才可以最大化赛道条数。
让我们举一个例子。
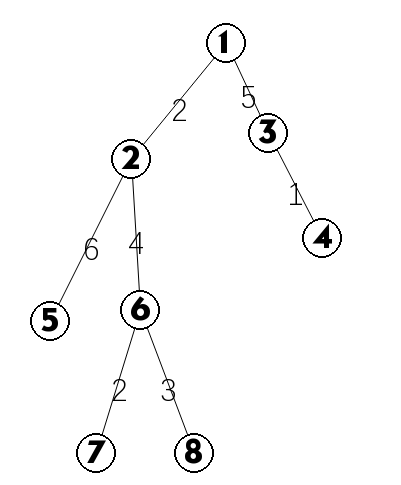
对于上面这棵树,我们先从它最底层的子树说起,就比如 \(6,7,8\) 这棵子树。
如果一条赛道包含有这一棵子树中的边,那么这条赛道可能有如下两种情况:
- 这条赛道的全部部分都由这棵子树中的边组成。
- 这条赛道的一端有部分边由这条子树中的边组成,剩下的部分由节点 \(6\) 以上(不在这棵子树中)的边组成。
如果说得易懂一些,那么就是,从这棵子树中的某一个顶点一直向上伸过来,到达子树根 \(6\),对于第一种情况,他越过顶点 \(6\),去往外探索世界,对于第二种情况,他折回头继续去这棵子树当中的其他分支延伸开去。
当然,还有一种比较特殊的情况,就是刚好它到了 \(6\) 这里长度大于等于我们二分到的这个值,它就不需要再去探索其他的边了,我们就把它记做一条赛道。
图解:
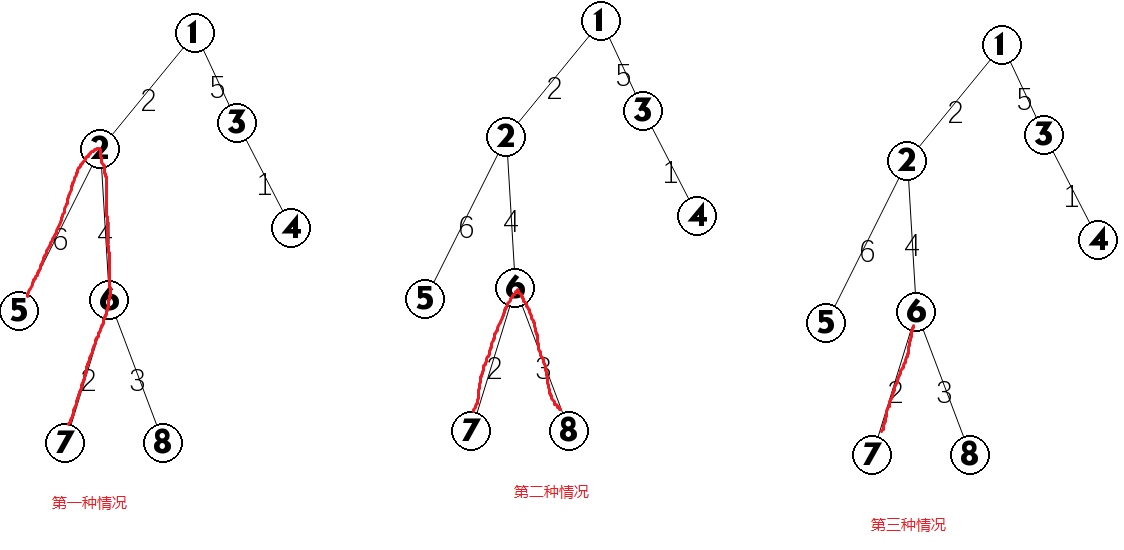
我们考虑:首先,去在这棵子树里找两个分支,使得他们边权之和大于等于 \(mid\);这一步我们应该尽量“节省”,比如说我们有 \(3\ 4\) 和 \(3\ 5\) 两种合法的选择,我们就应该选择 \(3\ 4\),为后面留下更多的空间。然后,在剩下的无法配对的分支当中,选取边权最大的一个,呈献给我们的根节点,这样,当我们像这样子去操作上面的 \(2,5,6\) 这个子树时,\(6\) 这个子节点所能达到的最优分支长度就应该是 边 2-6 的长加上我们呈献给 \(6\) 的子分支长度 的和。
策略阶段
我们有了大概的思路,应该想想什么样策略适合计算机去实现。
- 对整棵树进行遍历,把输入的无向图整合成一棵树,方便后面实现,同时记录每个节点的:父亲,儿子及到这个儿子的边之长。
- 算出这棵树的直径,二分答案的上界就应该是它——因为赛道是一条链,所以答案一定不会超过树的直径。(树的直径就是一棵树上最长的从一点到一点的路径长度,常用的求树的直径的方法是,从树上任意一点找到一个树上距离它最远的点,然后找到从这个最远点开始的树上路径中最长的长度。)
- 每个节点有一个 \(\text{set}\),储存这个节点为根的子树的所有分支,当然,我们只需要在 \(\text{set}\) 中放那些需要组合的,也就是说他自己一个人不足赛道长的分支,如果是我们刚才说的第三种情况,那我们直接说我们多了一条赛道就好了(不需要放入 \(\text{set}\))。
- 然后在 \(\text{set}\) 中进行配对(配成一对就加了一条赛道),配不成的就取 \(\max\) 然后贡献给根,我们把每个节点得到的贡献记为 \(val\)。
- 最后检查一下是不是赛道数大于等于 \(m\),如果是,这个 \(mid\) 合法(\(L=mid\)),否则,\(mid\) 不合法(\(R=mid\))。最终的 \(L\) 即是答案。
代码阶段
有了清晰的思路,代码应该比较好写了,但是还是有一些地方需要注意。
- 加快读
- 开 O2
- 然后我们就可以 AC 了
代码有简要注释。
#pragma GCC optimize(2) //O2优化
#include <bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int n,m,cnt,val[N],u[N],v[N],w[N],book[N],fa[N],Max,V;
//n,m如题所述,cnt用来记每次二分到的值对应合法赛道数
//u,v,w是题目输入的两个顶点、一条边长
//book是在还没有把树造出来的情况下用来记录dfs时哪些点走过没有
struct race {
int node,edge; //顶点编号、边长
};
vector<int> _g[N];
vector<race> W[N];
vector<race> G[N];
multiset<int> s[N];
multiset<int>::iterator it;
void dfs(int step,int k){
int x=0;
s[step].clear();
for(int i=0;i<G[step].size();i++){
dfs(G[step][i].node,k);
if(val[G[step][i].node]+G[step][i].edge>=k)
cnt++;
else
s[step].insert(val[G[step][i].node]+G[step][i].edge);
}
while(!s[step].empty()){
if(s[step].size()==1){ //只剩一个顶点没有处理了,取个max呈献给根
val[step]=max(x,*s[step].begin());
return;
}
it=s[step].lower_bound(k-*s[step].begin()); //第一个和s.begin()相加能大于等于k的
if(it==s[step].begin() && s[step].count(*it)==1) it++; //如果是自己那没办法只能找后面一个
if(it==s[step].end()){ //没有合适的也就是说配不了对
x=max(x,*s[step].begin()); //按照我们之前说的找一个个儿大的
s[step].erase(s[step].find(*s[step].begin())); //处理过的就要删掉
}
else {
cnt++; //配成一对儿
//同样,配成对的两个不能再用了,删掉
s[step].erase(s[step].find(*it));
s[step].erase(s[step].find(*s[step].begin()));
}
}
val[step]=x; //呈现给子树根
return;
}
bool check(int k){
cnt=0;
dfs(1,k);
return cnt>=m;
}
void init(int step){ //把父节点什么的整合出来
book[step]=1;
for(int i=0;i<_g[step].size();i++)
if(!book[_g[step][i]]){
fa[_g[step][i]]=step;
init(_g[step][i]);
}
return;
}
int read(){ //快速读入
int x=0;
char ch=getchar();
while(ch<'0' || ch>'9') ch=getchar();
while(ch>='0' && ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void getdis(int step,int sum){ //找从一个点出发的最远点
book[step]=1;
if(sum>Max) V=step,Max=sum; //V是最远点,Max是最长路径长度
for(int i=0;i<W[step].size();i++)
if(!book[W[step][i].node])
getdis(W[step][i].node,sum+W[step][i].edge);
}
int tree_D(){ //返回值就是树的直径
Max=0;
memset(book,0,sizeof(book));
getdis(1,0);
Max=0;
memset(book,0,sizeof(book));
getdis(V,0);
return Max;
}
int main()
{
n=read(),m=read();
race t;
for(int i=1;i<=n-1;i++){
u[i]=read(),v[i]=read(),w[i]=read();
_g[u[i]].push_back(v[i]);
_g[v[i]].push_back(u[i]);
t.node=v[i],t.edge=w[i];
W[u[i]].push_back(t);
t.node=u[i],t.edge=w[i];
W[v[i]].push_back(t);
}
init(1);
//以上是一些基础树上操作,不赘述
for(int i=1;i<=n-1;i++){ //把无向图整合成一棵树
//G[x]是x的所有儿子和分别到他们的距离
if(fa[u[i]]==v[i]){
t.node=u[i],t.edge=w[i];
G[v[i]].push_back(t);
}
else {
t.node=v[i],t.edge=w[i];
G[u[i]].push_back(t);
}
}
int L=1,R=tree_D()+1,mid;
while(L<R-1){
mid=(L+R)/2;
if(check(mid)) L=mid;
else R=mid;
}
printf("%d\n",L); //输出答案
return 0;
}
希望你能收获更多!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号