平衡树1
简介
Treap 是 Tree 与 Heap 的合并词,是一种比较基础的平衡树。
BST,即二叉搜索树,是一种支持插入、删除、多种查询的数据结构,操作的期望复杂度均为 \(O(\log n)\)。它每个节点有一个键值,它的性质是:任节点左儿子为根的子树中所有节点的键值<该节点键值<右儿子为根的子树中所有节点的键值。通常不构造两个键值相同的节点,因此上面的小于号没有带等;如果必须插入两个相同的键值,建议在原有节点上记录其出现次数,也就是该键值所对节点的出现次数为 2。
容易发现:BST 的中序遍历是单调递增的序列。
BST 的插入操作:从根节点出发,如果要插入的值小于当前节点的值则在左子树中递归插入,如果等于就把出现次数加一并回溯,如果大于就在右子树中递归插入;如果某时刻被牵着鼻子走到的当前节点为空就在这里新建节点,键值设为要插入的值,然后回溯。
查询操作,同理。
删除操作:找到要删除的节点,如果出现次数大于 1 就直接将出现次数减一。否则:如果该节点只有左儿子或右儿子,就令它代替该节点的位置。若不是,找到该节点的后继节点,容易发现,这个节点没有左子节点,因此直接删除它然后让它代替原节点。
所谓前驱、后继是指键值小于这个节点键值的所有节点中键值最大的一个,以及键值大于这个节点键值的所有节点中键值最小的一个。注意最小键值的节点没有前驱,最大键值的节点没有后继。为此避免判断边界,我们一般在 BST 中额外添两个点 -INF 和 INF,初始化 BST 根为-INF,根的右儿子为 INF。
查目标节点的前驱:从根节点出发找目标节点,用途中经过的节点更新前驱,找到后:如果它有左儿子,到它左儿子那里去,然后一直走向右儿子走到尽头,尽头的节点就是前驱;没有左儿子,更新到现在的那个答案就是前驱。
查后继,同理。
我们发现,当插入一系列值而这些值是单调上升或单调下降时,BST 会退化成一条链。怎么办呢?这时平衡树就出现了。平衡树就是一棵“平衡”的 BST。所谓平衡顾名思义,比如,自然一棵满二叉树就比一条链要平衡。如何将一棵树变得平衡呢?我们引入旋转这个概念。
单旋转
单旋转是 Treap 的核心操作之一。单旋转分为右旋 zig 和 左旋 zag。以原来处于父节点位置的节点作为主语,它旋转后相对位置靠右,而左旋后相对位置靠左。以一个节点为主语进行左右旋他旋转后相对位置靠下。
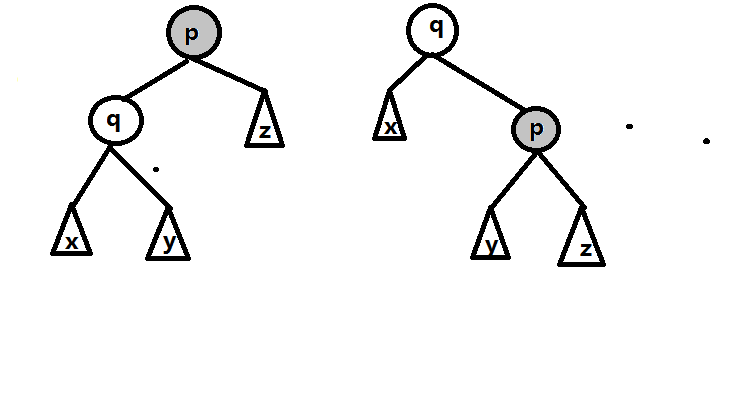
叫做单旋转因为只旋转了一次,还有双旋转不过不是 Treap 这节里的。
我们发现要使它还满足 BST 性质,必须要向如图所示那样连接新状态下的节点和子树。我们归纳左旋为三部,右旋也同理:
(1)让 y 成为 p 的左儿子(2)让 p 成为 q 的右儿子(3)让 q 代替 p 的位置,或,让 q 成为原来 p 的父亲的孩子。使用引用可以在代码中省去 p 的父节点的判断。
void zig(int &p){
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p;
p=q;
Update(a[p].r),Update(p);
}
void zag(int &p){
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p;
p=q;
Update(a[p].l),Update(p);
}
单单旋转好像没有什么带来什么区别。发明 Treap 的人想到大根堆的性质,然后给每个节点多加了一个键值,我们姑且称这个键值为附加值,每个节点的附加值让它随机产生,因为一棵随机的 BST 可以看作总是平衡的。根据附加值让 Treap 总满足大根堆性质,这也是为什么它名字里有 Heap 的原因。
我们在 Treap 中插入节点并赋一个附加值就需要时时调整结构使满足堆性质。因为可以旋转我们考虑删除操作不那么复杂,可直接把要删除的点旋到叶子,并直接删除。注意反悔的时候要维护堆。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5,INF=1e9;
struct Treap {
int l,r;
int val,dat;
int cnt,size;
}a[N]; int root,tot;
int New(int val){
a[++tot].val=val;
a[tot].dat=rand();
a[tot].cnt=a[tot].size=1;
return tot;
}
void Update(int p){
a[p].size=a[a[p].l].size+a[a[p].r].size+a[p].cnt;
}
void Build(){
New(-INF),New(INF);
root=1,a[1].r=2;
Update(root);
}
void zig(int &p){
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p;
p=q;
Update(a[p].r),Update(p);
}
void zag(int &p){
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p;
p=q;
Update(a[p].l),Update(p);
}
void Insert(int &p,int val){
if(p==0){
p=New(val);
return;
}
if(val==a[p].val){
a[p].cnt++,Update(p);
return;
}
if(val<a[p].val){
Insert(a[p].l,val);
if(a[p].dat<a[a[p].l].dat) zig(p);
}
else {
Insert(a[p].r,val);
if(a[p].dat<a[a[p].r].dat) zag(p);
}
Update(p);
}
void Remove(int &p,int val){
if(p==0) return;
if(val==a[p].val){
if(a[p].cnt>1){
a[p].cnt--,Update(p);
return;
}
if(a[p].l || a[p].r){
if(a[p].r==0 || a[a[p].l].dat>a[a[p].r].dat)
zig(p),Remove(a[p].r,val);
else zag(p),Remove(a[p].l,val);
Update(p);
}
else p=0;
return;
}
val<a[p].val?Remove(a[p].l,val):Remove(a[p].r,val);
Update(p);
}
int GetPre(int val){
int ans=1;
int p=root;
while(p){
if(val==a[p].val){
if(a[p].l>0){
p=a[p].l;
while(a[p].r>0) p=a[p].r;
ans=p;
}
break;
}
if(a[p].val<val && a[p].val>a[ans].val) ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
int GetNext(int val){
int ans=2;
int p=root;
while(p){
if(val==a[p].val){
if(a[p].r>0){
p=a[p].r;
while(a[p].l>0) p=a[p].l;
ans=p;
}
break;
}
if(a[p].val>val && a[p].val<a[ans].val) ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
int GetRankByVal(int p,int val){
if(p==0) return 0;
if(val==a[p].val) return a[a[p].l].size+1;
if(val<a[p].val) return GetRankByVal(a[p].l,val);
return GetRankByVal(a[p].r,val)+a[a[p].l].size+a[p].cnt;
}
int GetValByRank(int p,int rank){
if(p==0) return INF;
if(rank<=a[a[p].l].size) return GetValByRank(a[p].l,rank);
if(rank<=a[a[p].l].size+a[p].cnt) return a[p].val;
return GetValByRank(a[p].r,rank-a[a[p].l].size-a[p].cnt);
}
int main()
{
int m;
cin>>m;
Build();
int opt,x;
while(m--){
cin>>opt>>x;
switch(opt){
case 1:
Insert(root,x);
break;
case 2:
Remove(root,x);
break;
case 3:
cout<<GetRankByVal(root,x)-1<<'\n'; //-1是因为-INF占了一个rank
break;
case 4:
cout<<GetValByRank(root,x+1)<<'\n'; //+1是因为-INF是"rank 1"
break;
case 5:
cout<<GetPre(x)<<'\n';
break;
case 6:
cout<<GetNext(x)<<'\n';
break;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号