线段树1
线段树(Segment Tree),是一种支持单点/区间修改、满足结合律的询问(如求和、最值等)的数据结构。
下图可以大体表示线段树的工作原理。
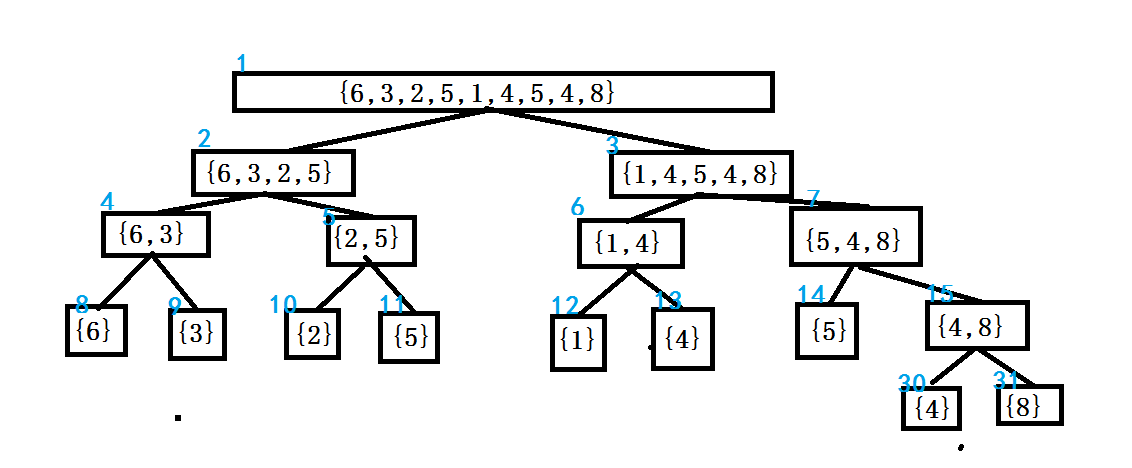
解释:
容易看出最顶上的是原数组,每个叶子节点依次是一个单个的数组元素。而对于每个非叶子节点,将其分解为两半——假使这个节点储存的是 \([l,r]\) 区间,那么左子节点存储的则是 \([l,mid]\),右子节点是 \([mid+1,r]\),其中 \(mid\) 为他们的正中央,即 \(\lfloor\frac{l+r}{2}\rfloor\)。关于编号:可以方便地得出编号为 \(k\) 的节点的左右子节点编号为 \(2k,2k+1\);使用位运算更加快捷,即 k<<1,k<<1|1。对于线段树,每个节点除了有一个编号和一个子数组,还需要存储 \([l,r]\) 的答案,供询问和修改所用(要不建这么大一棵树干嘛),用 \(t_k\) 表示节点 \(k\) 的答案。
下面以区间加(修改)与(询问)区间求和为例来阐述线段树的工作过程。
5 4
3 6 2 1 9
1 2 5 2
2 1 4
1 1 3 5
2 2 4
假设上面是输入:第一行是 \(n,m\) 代表数列长度和询问个数。第二行 \(n\) 个数代表数列。最后 \(m\) 行每行一个询问——
1 l r x代表对区间 \([l,r]\) 内所有数加个 \(x\)。2 l r代表询问 \([l,r]\) 中所有数之和。
一、建树
const int N=5e6+5;
int a[N],t[N],lazy[N];
void pushup(int k){
t[k]=t[k<<1]+t[k<<1|1];
}
void build(int l,int r,int k){
if(l==r) t[k]=a[l];
else {
int mid=(l+r)/2;
build(l,mid,k<<1);
build(mid+1,r,k<<1|1);
pushup(k);
}
}
解释:
- a:原数组 t:线段树
- build: 建树函数。思路是,首先把左右儿子都建了,然后把它们的 t 给加起来于是得到 k 的 t,就建好了。如果这棵子树就是叶子结点(l==r),那么显然它的 t 就等于 a[l]。
- pushup: 整合函数,就是把左右儿子的值整合一下传给当前的 k。
二、修改
void pushdown(int l,int r,int k){
if(lazy[k]){
lazy[k<<1]+=lazy[k];
lazy[k<<1|1]+=lazy[k];
int mid=(l+r)/2;
t[k<<1]+=lazy[k]*(mid-l+1);
t[k<<1|1]+=lazy[k]*(r-mid);
lazy[k]=0;
}
}
void updata(int L,int R,int v,int l,int r,int k){
if(L<=l && r<=R){
lazy[k]+=v;
t[k]+=v*(r-l+1);
}
else {
pushdown(l,r,k);
int mid=(l+r)/2;
if(L<=mid) updata(L,R,v,l,mid,k<<1);
if(R>mid) updata(L,R,v,mid+1,r,k<<1|1);
pushup(k);
}
}
- lazy: 如果现在对编号 k 的区间加上了 x 但是现在还没有问到 k 或 k 的子孙们的答案,那就省一时的力,暂且给 k 打上一个叫做 lazy 的标签,代表“此节点还有多少需要加但偷懒还没有加的值”,所以只需要 lazy[k]+=x 就好了。
- pushdown: 如果 k 还有偷懒没加的值,就把他给处理掉:首先下发给它的儿子们(因为 [l,r]+=x 就相当于 [l,mid]+=x,[mid+1,r]+=x 了),然后他的儿子们如果需要用到实际值(不能再偷懒了)就把他们的lazy处理掉,不需要用就储存在他们的 lazy 里,总之 lazy[k] 是已经没有负担了。
- updata: 修改函数。如果这个区间完全包含于要修改的区间 [L,R] 内,说明他可以偷懒,只用把 lazy 加上 v 就好了。那么如果不是完整的包含在要修改的区间内,比如说修改的是 [3,5] 但当前的是 [1,4],那么就需要先修改他的儿子们再传给他自己。当然,修改他的儿子之前,需要先把 lazy[k] 处理掉,就好比可以暂且不干活的时候就偷懒不干活,不能不干活的时候就干脆一气全部干了,以求一劳永逸。
三、询问
int query(int L,int R,int l,int r,int k){
pushdown(l,r,k);
if(L<=l && r<=R) return t[k];
else {
int mid=(l+r)/2;
int res=0;
if(L<=mid) res+=query(L,R,l,mid,k<<1);
if(R>mid) res+=query(L,R,mid+1,r,k<<1|1);
return res;
}
}
结构与 updata() 类似,这里不赘述。
四、完整代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e6+5;
int a[N],t[N],lazy[N];
void pushup(int k){
t[k]=t[k<<1]+t[k<<1|1];
}
void build(int l,int r,int k){
if(l==r) t[k]=a[l];
else {
int mid=(l+r)/2;
build(l,mid,k<<1);
build(mid+1,r,k<<1|1);
pushup(k);
}
}
void pushdown(int l,int r,int k){
if(lazy[k]){
lazy[k<<1]+=lazy[k];
lazy[k<<1|1]+=lazy[k];
int mid=(l+r)/2;
t[k<<1]+=lazy[k]*(mid-l+1);
t[k<<1|1]+=lazy[k]*(r-mid);
lazy[k]=0;
}
}
void updata(int L,int R,int v,int l,int r,int k){
if(L<=l && r<=R){
lazy[k]+=v;
t[k]+=v*(r-l+1);
}
else {
pushdown(l,r,k);
int mid=(l+r)/2;
if(L<=mid) updata(L,R,v,l,mid,k<<1);
if(R>mid) updata(L,R,v,mid+1,r,k<<1|1);
pushup(k);
}
}
int query(int L,int R,int l,int r,int k){
pushdown(l,r,k);
if(L<=l && r<=R) return t[k];
else {
int mid=(l+r)/2;
int res=0;
if(L<=mid) res+=query(L,R,l,mid,k<<1);
if(R>mid) res+=query(L,R,mid+1,r,k<<1|1);
return res;
}
}
signed main()
{
int n,m,opt,l,r,c;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,n,1);
while(m--){
cin>>opt;
if(opt==1) cin>>l>>r>>c,updata(l,r,c,1,n,1);
else cin>>l>>r,cout<<query(l,r,1,n,1)<<endl;
}
return 0;
}
这是一道线段树模板(link),还有一些练习题可以参照以下链接:
感谢观看!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号