矩阵乘法

矩阵乘法是一种最为常见的矩阵运算，一个 \(n\times m\) 的矩阵和一个 \(m\times p\) 的矩阵可以进行矩阵乘法；矩阵乘法满足结合律（\(A\times B\times C=(A\times B)\times C=A\times (B\times C)\)），但不满足交换律（\(A\times B\neq B\times A\)）。矩阵可以进行幂运算，并且可以用快速幂计算。

矩阵快速幂

void mul(int a[N],int b[N][N]){
    int c[N];
    memset(c,0,sizeof(c));
    for(int i=0;i<N;i++)
        for(int j=0;j<N;,j++)
            for(int k=0;k<N;k++)
                c[i][j]+=a[i][k]*b[k][j];
    memcpy(a,c,sizeof(c));
}
void mulself(int a[N][N]){
    int c[N][N];memset(c,0,sizeof(c));
    for(int i=0;i<N;i++)
        for(int j=0;j<N;,j++)
            for(int k=0;k<N;k++)
                c[i][j]+=a[i][k]*a[k][j];
    memcpy(a,c,sizeof(c));
}
int PowerMod(int a[N][N],int b){
    int ans[N]={...};
    while(b){
        if(b&1) mul(ans,a);
        b>>=1,mulself(a);
    }
    return ...;
}

矩阵加速 DP

一般步骤为：

设置（一维，\(1\times k\) 的）状态矩阵：举个例子，如果 \(F_n\) 受 \(F_{n-1},F_{n-2}\) 影响，那么建立状态矩阵为 \(\begin{bmatrix}F_{n-1} & F_{n}\end{bmatrix}\)。
设置（二维，\(k\times k\) 的）转移矩阵：把你列出的转移方程式用转移矩阵中的常数表示出来；沿用刚才的例子，如果转移方程式为 \(F_n=F_{n-1}+F_{n-2}\)，那么转移矩阵为 \(\begin{bmatrix}0 & 1\\ 1&1\end{bmatrix}\)，因为 \(\begin{bmatrix}F_{n-1} & F_{n}\end{bmatrix}\times\begin{bmatrix}0 & 1\\ 1&1\end{bmatrix}=\begin{bmatrix}F_{n} & F_{n+1}\end{bmatrix}\)。我们发现：如果状态矩阵中，转移之前的第 \(x\) 位置对转移之后的第 \(y\) 位置有影响，那么把转移矩阵的 \((x,y)\) 位置填上 \(k\)，其中 \(k\) 表示 \(<y>\) 要加上 \(<x>\) 的系数；最终，把转移矩阵中剩下的位置都填 \(0\)。

【例】斐波那契数列
斐波那契数列有两个性质：（1）\(F_i = {F_{i-1}} + {F_{i-2}}\)（2）\(\sum_{i=1}^n F_i= F_{n+2}\)。

求 \(Fib_n\)（从 1 开始标号）。
其实我们上边刚才举的例子，就是跟这题一样的，下面直接上代码。

#include <bits/stdc++.h>
using namespace std;
const long long Mod=1e9+7;
void mul(long long a[2],long long b[2][2]){
    long long c[2];
    memset(c,0,sizeof(c));
    for(int i=0;i<2;i++) 
        c[i]=(a[0]*b[0][i]%Mod+a[1]*b[1][i]%Mod)%Mod;
    memcpy(a,c,sizeof(c));
}
void mulself(long long a[2][2]){
    long long c[2][2];memset(c,0,sizeof(c));
    for(int i=0;i<2;i++)
        for(int j=0;j<2;c[i][j]%=Mod,j++)
            for(int k=0;k<2;k++)
                c[i][j]+=a[i][k]*a[k][j]%Mod;
    memcpy(a,c,sizeof(c));
}
long long PowerMod(long long a[2][2],long long b){
    long long ans[2]={1,1};
    while(b){
        if(b%2) mul(ans,a);
        b/=2,mulself(a);
    }
    return ans[0];
}
int main()
{
    long long n;
    cin>>n;
    long long a[2][2]={{0,1},{1,1}};
    cout<<PowerMod(a,n-1);
}

【练】link

经典题：逼死强迫症

拿到这题，第一想法是状压，用 \(F_{i,j}\) 表示填满 \(2\times i\) 的方格图的方案数，对于最后一列（第 \(i\) 列），\(j=0,1,2,3,4\) 分别表示：不填，左边填一个，右边填一个，两边各填一个，竖着放一个。这样我们就可以求出没有 \(1\times 1\) 的砖块时填满的方案数为 \(F_{n,0}+F_{n,4}\)。那现在有分裂的砖啊！我们用 \(dp_i\) 表示将其中一块 \(1\times 1\) 的砖放在第 \(i\) 列，另外一块放在 \(1\sim i\) 列之间，恰好铺满 \(2\times i\) 的区域的方案数。我们发现 \(dp_{i-1}\) 已经帮 \(dp_i\) 做了很大一部分工作，现在我们只需考虑如何转移。
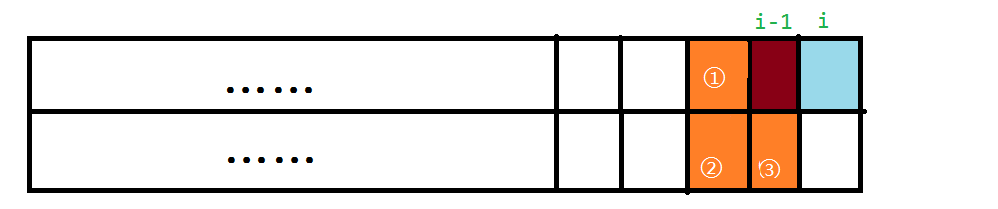
图片.png
我们发现当 \(i-1\) 时填上棕色那块时，①②③三个块块我们是不会选择去用另一个 \(1\times 1\) 填它的；那 \(i\) 时是否可以填呢？我们发现 \(i\) 时②块是可以填的，填上后增加的方案数为 \(F_{i-3,0}+F_{i-3,4}\)。因此转移方程为
\(dp_{i}=dp_{i-1}+2(F_{n,0}+F_{n,4})\)（乘2是因为翻过来又有一种情况）。多嘴一下，初始有 \(dp_1=dp_2=0,dp_3=2,G_0=1\)。我们奇妙地发现，\(F_{n,0}+F_{n,4}=fib_{n+1}\)，是斐波那契数列！而根据组合数学，我们最终的答案应该是 \(\sum _{i=1}^n dp_i\times (F_{n-i,0}+F_{n-i,4})\)。代码1：（用的是状压求 \(F_0+F_4\)）
link
Result: 50pts, TLE/RE.

然后我们把 \(G_i=fib_{i+1}\) 代入得到了更糟的结果（20pts+3TLE+4RE），这里不展示代码了。

第二步，

\[dp_n=dp_{n-1}+2fib_{n-2}=dp_{n-2}+2fib_{n-3}+2fib_{n-2}=\cdots=2\sum_{i=1}^{n-2}fib_i=2(fib_n-1) \]

\[ans=\sum _{i=1}^n dp_i\times fib_{n-i+1}=2 \sum_{i=1}^n (fib_i-1)\times fib_{n-i+1}=2\cdot(1+\sum_{i=1}^n fib_i\times fib_{n-i+1}-\sum_{i=1}^n fib_{n-i+1})=2\cdot(1-fib_{n+2}+\sum_{i=1}^n fib_i\times fib_{n-i+1}) \]

代码2：link

第三步，
令 \(G_i=\sum_{i=1}^n fib_i\times fib_{n-i+1}\)，则 \(G_i=\sum_{i=1}^n fib_i\times fib_{n-i+1}=fib_n+\sum_{i=1}^{n-1} fib_i\times (fib_{n-i}+fib_{n-i+1}-fib_{n-i})=fib_n+\sum_{i=1}^{n-1} fib_i\times (fib_{n-i}+fib_{n-i-1})=fib_n+\sum_{i=1}^{n-1} fib_i\times fib_{n-i}+\sum_{i=1}^{n-2}fib_{(n-2)-i+1}=G_{n-1}+G_{n-2}+fib_n\)。真是有种拨云见日的感觉！

有这个转移方程式，得到矩阵的转移式：

\[\begin{bmatrix}fib_{n-1} fib_n G_{n-1} G_n\end{bmatrix} \]

\[\times \begin{bmatrix}0&1&0&1\\1&1&0&1\\0&0&0&1\\0&0&1&1\end{bmatrix} \]

\[=\begin{bmatrix}fib_n fib_{n+1} G_n G_{n+1}\end{bmatrix} \]

代码3(Final)：（复杂度 \(O(4^3\log n)\)）

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int Mod=1e9+7;
void mul(int a[4],int b[4][4]){
    int c[4]; memset(c,0ll,sizeof(c));
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            c[i]=(c[i]+a[j]*b[j][i]%Mod)%Mod;
    memcpy(a,c,sizeof(c));
}
void mulself(int a[4][4]){
    int c[4][4]; memset(c,0ll,sizeof(c));
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            for(int k=0;k<4;k++)
                c[i][j]=(c[i][j]+a[i][k]*a[k][j]%Mod)%Mod;
    memcpy(a,c,sizeof(c));
}
void PowerMod(int b){
    int ans[4]={0,1,0,1};
    int a[4][4]={{0,1,0,1},{1,1,0,1},{0,0,0,1},{0,0,1,1}};
    while(b){
        if(b%2ll) mul(ans,a);
        b/=2ll,mulself(a);
    }
    int Ans=2ll*((ans[3]+Mod-(ans[0]+ans[1]*2ll%Mod)%Mod+1ll)%Mod)%Mod;
    //一定注意这里的"+Mod"，因为ans[3]和后面那堆都是%过Mod的，作差后不再一定为正数
	cout<<Ans<<endl;
}
void solve()
{
	int n;
	cin>>n;
	if(n<3){
		cout<<0<<endl; return;
	}
	PowerMod(n-1);
}
signed main(){
	int T; cin>>T;
	while(T--) solve();
	return 0;
}

posted @ 2021-06-30 18:41 pengyule 阅读(701) 评论(0) 编辑收藏举报

刷新页面返回顶部

pengyule 的博客

抬头看远方

矩阵乘法

矩阵快速幂

矩阵加速 DP

经典题：逼死强迫症