二叉堆
二叉堆是一棵完全二叉树。大根堆:对于每一棵子树,有他的根节点大于所有非根节点。小根堆则相反。请注意二叉堆不等同于二叉搜索树——其中序遍历并不一定有序。下图是一个小根堆:
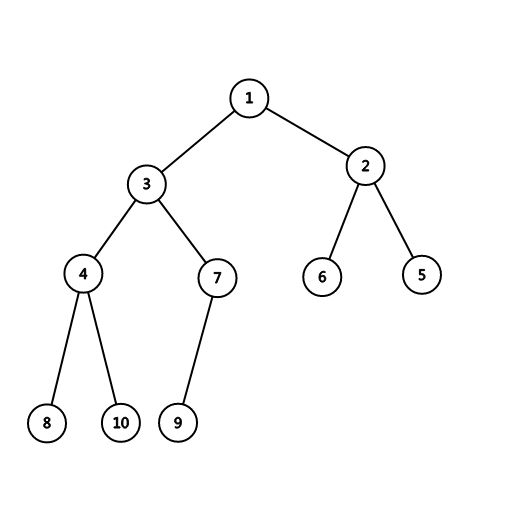
堆的存在可以让我们快捷地找到他的最值(小根堆:最小值;大根堆:最大值;同时不必局限于数字的大小,而可以拓广到依题目所定的优先级),即为堆顶(根)的值。我们可以对节点进行编号,从而快捷地找到一个节点的左子节点编号为自己的两倍,右子节点(如果有的话)为自己的两倍加一。可见一棵完全二叉树的高度为节点个数 \(n\) 以二为底的对数 \(\log n\)。
堆还支持插入、删除操作。
插入
在上图的堆中再插入一个 \(1\) 应该怎么做?
首先我们应该意识到,这个堆可以用一个一维的数组储存:\(heap\{ 1,3,2,4,7,6,5,8,10,9\}\)。如上面所说,要找到 heap[3]=2 的左儿子 6 只需要 heap[3*2]=heap[6]=6。
我们可以暂且把待插入的 1 放到堆的最后一个元素之后,相当于是 7 的右儿子。发现 7 比 1 要大,不满足小根堆的性质,于是交换 1 和 7。这时又发现 3 比 1 要大,于是交换 1、3。这时发现 1 与 1 相等,不必互换,于是就放好了。
总结一下:
- 把待插入的数放到数组 heap 的末尾;
- 如果发现比他的父亲小,那么与他的父亲互换;重复这个判断步骤直至满足二叉堆的性质。
const int N=1e6+5;
int Size=0;
int heap[N];
void Add(int x){
heap[++Size]=x;
int now=Size,nxt;
while(now!=1){
nxt=now>>1;
if(heap[nxt]>heap[now]) swap(heap[now],heap[nxt]);
else break;
now=nxt;
}
}
删除
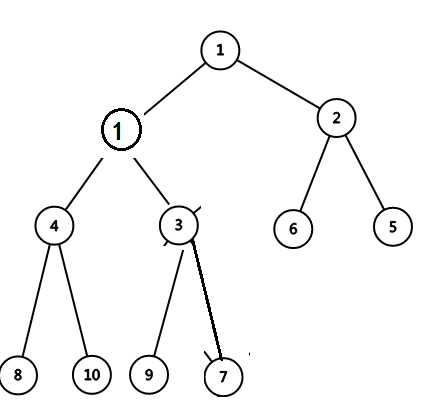
在上图删除堆顶的 \(1\) 应该怎么做?
肯定不可以直接把数组的第一个元素删除,因为这样会打乱整个堆。在代码实现中,首先将堆顶的 1 与数组末尾的 7 交换,然后踢掉现在居于数组末尾的 1。把堆顶的 7 进行调整:发现 7 比 1 和 2 都大,应该和谁交换呢?先试试跟 2 交换,发现此时 2 又比 1 大,于是成功地被绕晕了;再试试跟 1 交换,发现至少 [1,2,7] 这一块是满足堆的性质了,感到满意。所以记住了,当根比左右儿子大时,应该跟较小的那个交换。好,交换完了,又发现 7 比 4、3 大,于是交换 7、3。这时已经满足堆的性质了,删除操作执行完毕。
void Pop(){
swap(heap[1],heap[Size]);
Size--;
int now=1,nxt;
while((now<<1)<=Size){
nxt=now<<1;
if(nxt+1<=Size && heap[nxt+1]<heap[nxt]) nxt++;
if(heap[nxt]<heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
}
取堆顶最值
即 heap[1]。
完整代码
模板在 P3378。
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int Size=0;
int heap[N];
void Add(int x){
heap[++Size]=x;
int now=Size,nxt;
while(now!=1){
nxt=now>>1;
if(heap[nxt]>heap[now]) swap(heap[now],heap[nxt]);
else break;
now=nxt;
}
}
void Pop(){
swap(heap[1],heap[Size]);
Size--;
int now=1,nxt;
while((now<<1)<=Size){
nxt=now<<1;
if(nxt+1<=Size && heap[nxt+1]<heap[nxt]) nxt++;
if(heap[nxt]<heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
}
int main()
{
int n,opt,x;
cin>>n;
while(n--){
cin>>opt;
if(opt==1) cin>>x,Add(x);
if(opt==2) cout<<heap[1]<<endl;
if(opt==3) Pop();
}
//堆排序:
//while(Size--) cout<<heap[1]<<' ',Pop();
return 0;
}
练习
题面在 P1081 黑匣子。
朴素思路:建一个小根堆,对于每一次询问第 k 小值,首先进行 k-1 次删除操作,然后取堆顶,在把之前删过的元素放回去。这样复杂度太高了!据说只能得到 30pts。
正确思路:
- 建一个小根堆和一个大根堆;
- 我们可以把当前已有的数列中前 k 小的放入大根堆,那么堆顶显然就是第 k 小;
- 所以我们只需要在不断新加元素的过程中,让大根堆中永远是当前的前 k 小就好了;
- 循环嵌套,外层枚举 1~n。每次就把 \(a_{u_{i-1}+1}\sim a_{u_i}\) 全部加到小根堆中,然后再去看怎么样让大根堆中全部都是前 i 小,小根堆中全部都是其他;
- 我们把小根堆中最小的元素——堆顶放入大根堆,但这时并不一定满足,我们需作一定调整。如果小根堆的堆顶比大根堆的堆顶要小,那么说明小根堆中有比大根堆中要小的数,需要把大根堆的那个数移到小根堆来,小根堆中那个更小的数移到大根堆去。因此不断地交换小根堆堆顶和大根堆堆顶,直至小根堆堆顶大于等于大根堆堆顶;这样最后就可以维护大根堆。
- 维护完毕后输出大根堆堆顶,即为第 i 小。
- 复杂度:约 \(O(n+m+n\log m)\)。
代码实现:
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int a[N],u[N],ans[N];
struct smallheap {
int heap[N],Size;
void Add(int x){
heap[++Size]=x;
int now=Size,nxt;
while(now!=1){
nxt=now>>1;
if(heap[nxt]>heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
}
int Get(){
int res=heap[1];
swap(heap[1],heap[Size]);
Size--;
int now=1,nxt;
while((now<<1)<=Size){
nxt=now<<1;
if(nxt+1<=Size && heap[nxt+1]<heap[nxt]) nxt++;
if(heap[nxt]<heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
return res;
}
}s;
struct bigheap {
int heap[N],Size;
void Add(int x){
heap[++Size]=x;
int now=Size,nxt;
while(now!=1){
nxt=now>>1;
if(heap[nxt]<heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
}
int Get(){
int res=heap[1];
swap(heap[1],heap[Size]);
Size--;
int now=1,nxt;
while((now<<1)<=Size){
nxt=now<<1;
if(nxt+1<=Size && heap[nxt+1]>heap[nxt]) nxt++;
if(heap[nxt]>heap[now]) swap(heap[nxt],heap[now]);
else break;
now=nxt;
}
return res;
}
}t;
int main()
{
int m,n;
cin>>m>>n;
for(int i=1;i<=m;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>u[i];
s.Size=t.Size=0;
for(int i=1,j=1;i<=n;i++){
while(j<=u[i]) s.Add(a[j++]);
t.Add(s.Get());
int v1,v2;
while(s.Size && s.heap[1]<t.heap[1]){
v1=s.Get(),v2=t.Get();
s.Add(v2),t.Add(v1);
}
ans[i]=t.heap[1];
}
for(int i=1;i<=n;i++) cout<<ans[i]<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号