二叉树、红黑树、B树、B+树、图、Trie树合集-----妈妈再也不用担心我的“树”拉!
这里把各种树做个总结,分别介绍各个树是什么,什么原理,什么特点,什么情况下使用,另外很多时候它们很多地方是相似的,还要加以区别,之前我身边一个很多年开发的经验的老开发还以为B树、B-树、B+树是三种树,实际没有B-树,它实际就是B树,要是不区分清楚闹出这样的笑话就尴尬了。或者别人说“平衡树”、“满二叉树”、“3阶树”等概念时你一脸懵逼,想吹牛逼但是没词儿,那也挺尴尬,怎么办,一点一点学吧,下面一 一介绍。
一、树的基本术语
若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度:结点拥有的子树的数目。
叶子:度为零的结点(无子树的结点)。
分支结点:度不为零的结点。
树的度:树中结点的最大的度(下图中树的度即为3)。
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。
树的高度(树的深度):树中结点的最大层次。
无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。
有序树:如果树中结点的各子树之间的次序是重要的,各子树从左到右是有次序的,不可以交换位置。
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。



二、二叉树
2.1 定义
二叉树又叫二叉排序树(Binary Sort Tree),“二叉”就是树上的一根树枝开两个叉,而这棵树上的节点是已经排好序的,具体的排序规则如下:
- 若左子树不空,则左子树上所有节点的值均小于它的根节点的值
- 若右子树不空,则右字数上所有节点的值均大于它的根节点的值
- 它的左、右子树也分别为二叉排序数(递归定义)


上面的排序规则可以看出二叉树的特点,如果我们要查找某个元素,它可以使我们具有和二分法等同的效率,每经过一个节点就可以减少一半的可能,可以使我们的查询效率大幅提高。但是也会有比较极端的情况,那就是所有节点都位于同一侧,直观上看就是一条直线(这种树也叫斜树(左斜树),如上右图),这时查询效率就和原来的顺序查找一样了,效率很低,于是就有了“平衡二叉树”。
这里“平衡”要重点解释一下,说的是这棵树的各个分支的高度是均匀的,它的左子树和右子树的高度之差绝对值小于1,这样就不会出现一条支路特别长的情况。于是,在这样的平衡树中进行查找时,总共比较节点的次数不超过树的高度,这就确保了查询的效率(时间复杂度为O(logn))。
二叉树的应用:
- 哈夫曼编码,来源于哈夫曼树(给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为赫夫曼树(Huffman tree)。即带权路径长度最短的树),在数据压缩上有重要应用,提高了传输的有效性,详见《信息论与编码》。
- 海量数据并发查询,二叉树复杂度是O(K+LgN)。二叉排序树就既有链表的好处,也有数组的好处, 在处理大批量的动态的数据是比较有用。
2.2 满二叉树
这里还有几个常见的概念:
“满二叉树”:在一棵二叉树中若所有分支结点都存在左子树和右子树,且所有叶子都在同一层上,这样的二叉树称为满二叉树。
满二叉树的特点有:
- 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
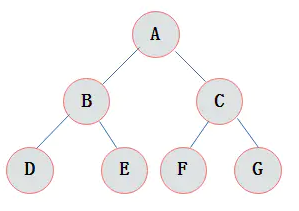
2.3 完全二叉树
“完全二叉树”:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。

叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树
2.4 二叉树的存储
二叉树有两种存储方式:顺序存储和链式存储
2.4.1 顺序存储
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。

上图所示的一棵完全二叉树采用顺序存储方式,可以这样表示:

同理,看下下面的右斜树:

顺序表示为:
![]()
其中,∧表示数组中此位置没有存储结点。此时可以发现,顺序存储结构中会有空间浪费的情况。因此顺序存储结构一般适用于完全二叉树。
2.4.2 链式存储
既然顺序存储不能满足二叉树的存储需求,那么考虑采用链式存储。节点表示成:
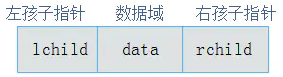
树可以表示为:

二叉链表结构灵活,操作方便,对于一般情况的二叉树,甚至比顺序存储结构还节省空间。因此,二叉链表是最常用的二叉树存储方式。
2.5 二叉树的遍历
二叉树有三种遍历方式:前序/中序/后续遍历
2.5.1 前(先)序遍历
所谓的先序遍历就是先访问根节点,再访问左节点,最后访问右节点。若二叉树为空,则退出。

上面的完全二叉树的前序遍历顺序就是:A、B、D、H、I、E、J、C、F、G
2.5.2 中序遍历
所谓的中序遍历就是先访问左节点,再访问根节点,最后访问右节点。若二叉树为空,则退出。

同样的完全二叉树的中序遍历顺序就是:H、D、I、B、J、E、A、F、C、G
2.5.3 后序遍历
所谓的后序遍历就是先访问左节点,再访问右节点,最后访问根节点。若二叉树为空,则退出。

同样的完全二叉树的中序遍历顺序就是:H、I、D、J、E、B、F、G、C、A
2.6 代码实例
上面概念、原理说了一大通了,该是动手用代码实现一下的时候了,Talk is cheap, show me the code。
package tree.binary;
import java.util.LinkedList;
import java.util.List;
/**
* @Author: GeFeng
* @Date: 2020年6月10日10:10:44
* @Description: 二叉树节点
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree bt = new BinaryTree();
bt.addNode(6);
bt.addNode(4);
bt.addNode(8);
bt.addNode(1);
bt.addNode(11);
bt.addNode(2);
bt.addNode(7);
System.out.println("【前序:】");
preOrder(bt.root);
System.out.println("【中序:】");
midOrder(bt.root);
System.out.println("【后序:】");
posOrder(bt.root);
}
/**
* 新建二叉树
*/
public static class BinaryTree {
BinaryTreeNode root;
public void addNode(int value) {
root = addNode(root, value);
}
private BinaryTreeNode addNode(BinaryTreeNode current, int value) {
if (current == null) {
return new BinaryTreeNode(value);
}
if (value < current.data) {
current.leftChild = addNode(current.leftChild, value);
} else if (value > current.data) {
current.rightChild = addNode(current.rightChild, value);
} else {
return current;
}
return current;
}
}
/**
* 前序遍历 根-> 左-> 右
* 递归
*/
public static void preOrder(BinaryTreeNode Node)
{
if (Node != null)
{
System.out.print(Node.getData() + " ");
preOrder(Node.getLeftChild());
preOrder(Node.getRightChild());
}
}
/**
* 中序遍历 左-> 根-> 右
* 递归
*/
public static void midOrder(BinaryTreeNode Node)
{
if (Node != null)
{
midOrder(Node.getLeftChild());
System.out.print(Node.getData() + " ");
midOrder(Node.getRightChild());
}
}
/**
* 后序遍历 左-> 右-> 根
* 递归
*/
public static void posOrder(BinaryTreeNode Node)
{
if (Node != null)
{
posOrder(Node.getLeftChild());
posOrder(Node.getRightChild());
System.out.print(Node.getData() + " ");
}
}
}

结果:
【前序: 根-> 左-> 右】
6 4 1 2 8 7 11
【中序: 左-> 根-> 右】
1 2 4 6 7 8 11
【后序: 左-> 右-> 根】
2 1 4 7 11 8 6 2.7 平衡二叉树
为什么最后一小节来介绍平衡二叉树呢?一是平衡二叉树是前面普通二叉树的升级版,放在最后做个升华;二是下面要介绍的红黑树和平衡二叉树有很多相似的地方,因此在这里介绍下,希望能承上启下。平衡二叉树是啥样的?见下图:

可见平衡二叉树的特点:
- 从任何一个节点出发,左右子树深度之差的绝对值不超过1。
- 左右子树仍然为平衡二叉树。
前面我们介绍了“左斜树”、“右斜树”,会造成查询效率低下的问题,一颗二叉查找树的优势完全丧失了。怎么办呢?既然上面的二叉查找树在插入的时候变成了“一条腿”,也就是丧失了平衡,那我们干脆做出一点改进,让它平衡一下。比如上面的平衡二叉树中我们要再插入一个4,按照普通的二叉树规则会出现下面的情况:

若按照平衡二叉树的要求,则会调整数的结构,使得整体满足平衡二叉树的规则:

平衡二叉树是高度平衡的,优势就是能够保持高效的查询效率;但是在插入和删除节点时因为要动态维护平衡,也会影响性能。
三、红黑树 —— RBTree
3.1 定义
上面说了平衡二叉树大量插入和删除节点的场景下,平衡二叉树为了保持平衡需要调整的频率会更高,性能会受到影响,这时红黑树成了首选。
红黑树其实就是一种数据结构,设计它的目的就是为了高效地进行增删改查,红黑树放弃了追求完全平衡,追求大致平衡,在与平衡二叉树的时间复杂度相差不大的情况下,保证每次插入最多只需要三次旋转就能达到平衡,实现起来也更为简单,而平衡二叉树追求绝对平衡,条件比较苛刻,实现起来比较麻烦,每次插入新节点之后需要旋转的次数不能预知。
所以在大量查找的情况下,平衡二叉树的效率更高,也是首要选择。在大量增删的情况下,红黑树是首选。
那到底啥是红黑树?看下图:

特性:
- 每个节点只有两种颜色:红色和黑色;
- 根节点是黑色的;
- 从根节点到叶子节点,不会出现两个连续的红色节点;
- 叶子节点都为黑色,且为 null;
- 从任何一个节点出发,到叶子节点,这条路径上都有相同数目的黑色节点。
因此不能就直接说红黑树不追求平衡,红黑树和平衡二叉树(AVL树)都是二叉查找树的变体,但红黑树的统计性能要好于AVL树。因为,AVL树是严格维持平衡的,红黑树是黑平衡的。维持平衡需要额外的操作,这就加大了数据结构的时间复杂度,所以红黑树可以看作是二叉搜索树和AVL树的一个折中,维持平衡的同时也不需要花太多时间维护数据结构的性质。
3.2 红黑树中的操作
红黑树的基本操作和其他树形结构一样,一般都包括查找、插入、删除等操作,不同的是因为要符合红黑树规则而多了旋转操作。旋转操作有分为左旋和右旋。
3.2.1 左旋
(盗的动态图,完美!)
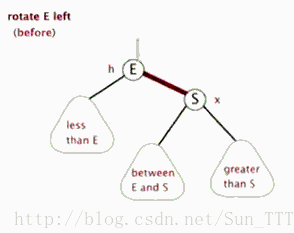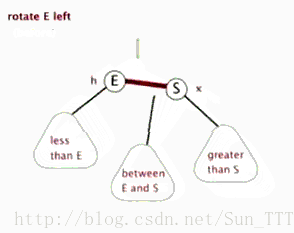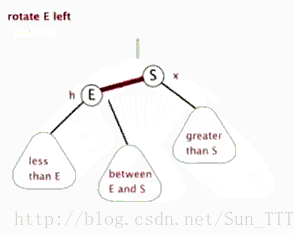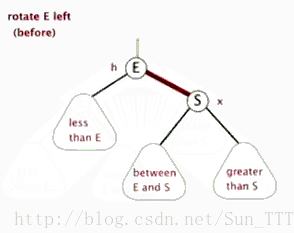

3.2.2 右旋
(还是盗的动态图,完美!)
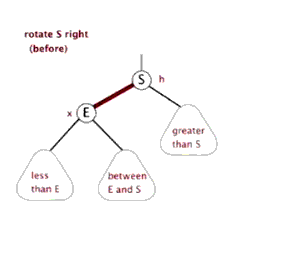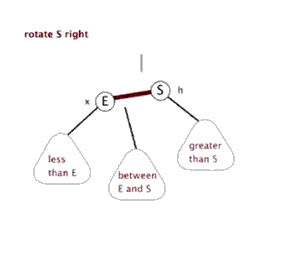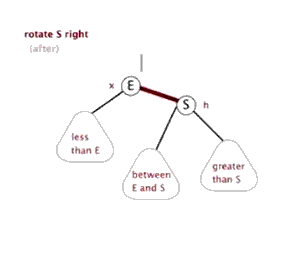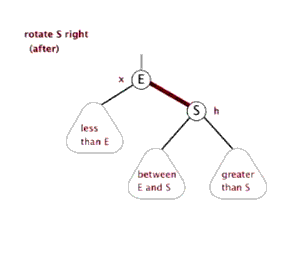


3.2.3 插入
红黑树的插入过程和二叉查找树插入过程基本类似,不同的地方在于,红黑树插入新节点后,需要进行调整,以满足红黑树的性质。
3.2.4 删除
红黑树的插入过程和二叉查找树插入过程基本类似,不同的地方在于,红黑树插入新节点后,需要进行调整,以满足红黑树的性质。相较于插入操作,红黑树的删除操作则要更为复杂一些。删除操作首先要确定待删除节点有几个孩子,如果有两个孩子,不能直接删除该节点。而是要先找到该节点的前驱(该节点左子树中最大的节点)或者后继(该节点右子树中最小的节点),然后将前驱或者后继的值复制到要删除的节点中,最后再将前驱或后继删除。
3.3 红黑树的应用
- linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
- 广泛用在C++的STL中,map和set都是用红黑树实现的
- epoll在内核中的实现,用红黑树管理事件块
- nginx中,用红黑树管理timer等
- Java的TreeMap、HashMap实现
上面可能比较陌生,不容易接触到,可以重点看下JDK里怎么应用的红黑树,这里重点介绍了HashMap中对红黑树的应用及实现:JAVA集合类(代码手写实现,全面梳理)_沙滩的流沙520的博客-CSDN博客_java集合代码。
3.4 红黑树代码实现
@Data
public class RBTreeNode {
private final boolean RED = false;
private final boolean BLACK = true;
private int key;
private boolean color;
private RBTreeNode left;
private RBTreeNode right;
private RBTreeNode parent;
}
@Data
public class RBTree {
RBTreeNode root;
private final boolean RED = false;
private final boolean BLACK = true;
public RBTreeNode query(int key) {
RBTreeNode tmp = root;
while (tmp != null) {
if (tmp.getKey() == key)
return tmp;
else if (tmp.getKey() > key)
tmp = tmp.getLeft();
else
tmp = tmp.getRight();
}
return null;
}
public void insert(int key) {
RBTreeNode node = new RBTreeNode(key);
if (root == null) {
root = node;
node.setColor(BLACK);
return;
}
RBTreeNode parent = root;
RBTreeNode son = null;
if (key <= parent.getKey()) {
son = parent.getLeft();
} else {
son = parent.getRight();
}
//find the position
while (son != null) {
parent = son;
if (key <= parent.getKey()) {
son = parent.getLeft();
} else {
son = parent.getRight();
}
}
if (key <= parent.getKey()) {
parent.setLeft(node);
} else {
parent.setRight(node);
}
node.setParent(parent);
//fix up
insertFix(node);
}
private void insertFix(RBTreeNode node) {
RBTreeNode father, grandFather;
while ((father = node.getParent()) != null && father.getColor() == RED) {
grandFather = father.getParent();
if (grandFather.getLeft() == father) { //F为G左儿子的情况,如之前的分析
RBTreeNode uncle = grandFather.getRight();
if (uncle != null && uncle.getColor() == RED) {
setBlack(father);
setBlack(uncle);
setRed(grandFather);
node = grandFather;
continue;
}
if (node == father.getRight()) {
leftRotate(father);
RBTreeNode tmp = node;
node = father;
father = tmp;
}
setBlack(father);
setRed(grandFather);
rightRotate(grandFather);
} else { //F为G的右儿子的情况,对称操作
RBTreeNode uncle = grandFather.getLeft();
if (uncle != null && uncle.getColor() == RED) {
setBlack(father);
setBlack(uncle);
setRed(grandFather);
node = grandFather;
continue;
}
if (node == father.getLeft()) {
rightRotate(father);
RBTreeNode tmp = node;
node = father;
father = tmp;
}
setBlack(father);
setRed(grandFather);
leftRotate(grandFather);
}
}
setBlack(root);
}
public void delete(int key) {
delete(query(key));
}
private void delete(RBTreeNode node) {
if (node == null)
return;
if (node.getLeft() != null && node.getRight() != null) {
RBTreeNode replaceNode = node;
RBTreeNode tmp = node.getRight();
while (tmp != null) {
replaceNode = tmp;
tmp = tmp.getLeft();
}
int t = replaceNode.getKey();
replaceNode.setKey(node.getKey());
node.setKey(t);
delete(replaceNode);
return;
}
RBTreeNode replaceNode = null;
if (node.getLeft() != null)
replaceNode = node.getLeft();
else
replaceNode = node.getRight();
RBTreeNode parent = node.getParent();
if (parent == null) {
root = replaceNode;
if (replaceNode != null)
replaceNode.setParent(null);
} else {
if (replaceNode != null)
replaceNode.setParent(parent);
if (parent.getLeft() == node)
parent.setLeft(replaceNode);
else {
parent.setRight(replaceNode);
}
}
if (node.getColor() == BLACK)
removeFix(parent, replaceNode);
}
//多余的颜色在node里
private void removeFix(RBTreeNode father, RBTreeNode node) {
while ((node == null || node.getColor() == BLACK) && node != root) {
if (father.getLeft() == node) { //S为P的左儿子的情况,如之前的分析
RBTreeNode brother = father.getRight();
if (brother != null && brother.getColor() == RED) {
setRed(father);
setBlack(brother);
leftRotate(father);
brother = father.getRight();
}
if (brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))) {
setRed(brother);
node = father;
father = node.getParent();
continue;
}
if (isRed(brother.getLeft())) {
setBlack(brother.getLeft());
setRed(brother);
rightRotate(brother);
brother = brother.getParent();
}
brother.setColor(father.getColor());
setBlack(father);
setBlack(brother.getRight());
leftRotate(father);
node = root;//跳出循环
} else { //S为P的右儿子的情况,对称操作
RBTreeNode brother = father.getLeft();
if (brother != null && brother.getColor() == RED) {
setRed(father);
setBlack(brother);
rightRotate(father);
brother = father.getLeft();
}
if (brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))) {
setRed(brother);
node = father;
father = node.getParent();
continue;
}
if (isRed(brother.getRight())) {
setBlack(brother.getRight());
setRed(brother);
leftRotate(brother);
brother = brother.getParent();
}
brother.setColor(father.getColor());
setBlack(father);
setBlack(brother.getLeft());
rightRotate(father);
node = root;//跳出循环
}
}
if (node != null)
node.setColor(BLACK);
}
private boolean isBlack(RBTreeNode node) {
if (node == null)
return true;
return node.getColor() == BLACK;
}
private boolean isRed(RBTreeNode node) {
if (node == null)
return false;
return node.getColor() == RED;
}
private void leftRotate(RBTreeNode node) {
RBTreeNode right = node.getRight();
RBTreeNode parent = node.getParent();
if (parent == null) {
root = right;
right.setParent(null);
} else {
if (parent.getLeft() != null && parent.getLeft() == node) {
parent.setLeft(right);
} else {
parent.setRight(right);
}
right.setParent(parent);
}
node.setParent(right);
node.setRight(right.getLeft());
if (right.getLeft() != null) {
right.getLeft().setParent(node);
}
right.setLeft(node);
}
private void rightRotate(RBTreeNode node) {
RBTreeNode left = node.getLeft();
RBTreeNode parent = node.getParent();
if (parent == null) {
root = left;
left.setParent(null);
} else {
if (parent.getLeft() != null && parent.getLeft() == node) {
parent.setLeft(left);
} else {
parent.setRight(left);
}
left.setParent(parent);
}
node.setParent(left);
node.setLeft(left.getRight());
if (left.getRight() != null) {
left.getRight().setParent(node);
}
left.setRight(node);
}
private void setBlack(RBTreeNode node) {
node.setColor(BLACK);
}
private void setRed(RBTreeNode node) {
node.setColor(RED);
}
private void inOrder(RBTreeNode node) {
if (node == null)
return;
inOrder(node.getLeft());
System.out.println(node);
inOrder(node.getRight());
}
}
四、B树
首先就要说明白,“B树”和“B-树”是一个哈,B-树不是一种新的树,不要多想。
4.1 为什么要有B树?
学习前首先问下为啥需要B树?已经有红黑树、二叉树等一堆多树了,又来个B树干啥?可以从下面几个方面考虑一下:
计算机有一个局部性原理,就是说,当一个数据被用到时,其附近的数据也通常会马上被使用。所以当你用红黑树的时候,你一次只能得到一个键值的信息,而用B树,可以得到最多M-1个键值的信息。这样来说B树当然更好了。另外一方面,同样的数据,红黑树的阶数更大,B树更短,这样查找的时候当然B树更具有优势了,效率也就越高。
4.2 为什么要有B树?
B树事实上是一种平衡的多叉查找树,也就是说最多可以开m个叉(m>=2),我们称之为m阶b树。
先盗个图:
一个m阶B树应该具备下面的特征:
- 根结点只有一个,分支数量范围为[2,m];
- 分支结点,每个结点包含分支数范围为[ceil(m/2), m];
- 所有的叶结点都在同一层上;
- 有 k 棵子树的分支结点则存在
k-1个关键码,关键码按照递增次序进行排列; - 每个结点关键字的数量范围为[ceil(m/2)-1, m-1]
(m阶指的是分叉的个数最多为m个,即一个非叶子节点最多可以有m个子节点。ceil表示向上取整,ceil(2.5)=3),下面是一个五阶B树:

这是一棵5阶的B树,每个节点的分支数在【3,5】之间,同时除根节点,一般节点所拥有的分支数也不得少于3;每个节点至多拥有4个关键码,除根节点外每个节点至少拥有2个关键码,结点内的关键字是有序的。
4.3 B树的查询规则
在B-树中查找给定关键字的方法是,首先把根结点取来,在根结点所包含的关键字K1,…,Kn查找给定的关键字(可用顺序查找或二分查找法),若找到等于给定值的关键字,则查找成功;否则,一定可以确定要查找的关键字在Ki与Ki+1之间,Pi为指向子树根节点的指针,此时取指针Pi所指的结点继续查找,直至找到,或指针Pi为空时查找失败。
4.4 B树代码实例
因为B树的特征比较多,所以它的代码比较复杂,首先建立节点内的Entry类:
/**
* B树节点中的键值对
*/
public class Entry<K, V> {
private K key;
private V value;
public Entry(K k, V v)
{
this.key = k;
this.value = v;
}
public K getKey()
{
return key;
}
public V getValue()
{
return value;
}
public void setValue(V value)
{
this.value = value;
}
@Override
public String toString()
{
return key + ":" + value;
}
}
在建立B树中的节点类(这里的Node类似HashMap的结构,新增/查询等也类似,可以参考):
package com.wo.domain.Btree;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
/**
* B树中的节点。
*/
public class BTreeNode<K, V>
{
/** 节点的项,按键非降序存放 */
private List<Entry<K,V>> entrys;
/** 内节点的子节点 */
private List<BTreeNode<K, V>> children;
/** 是否为叶子节点 */
private boolean leaf;
/** 键的比较函数对象 */
private Comparator<K> kComparator;
BTreeNode()
{
entrys = new ArrayList<Entry<K, V>>();
children = new ArrayList<BTreeNode<K, V>>();
leaf = false;
}
public BTreeNode(Comparator<K> kComparator)
{
this();
this.kComparator = kComparator;
}
public boolean isLeaf()
{
return leaf;
}
public void setLeaf(boolean leaf)
{
this.leaf = leaf;
}
/**
* 返回项的个数。如果是非叶子节点,根据B树的定义,
* 该节点的子节点个数为({@link #size()} + 1)。
* @return 关键字的个数
*/
public int size()
{
return entrys.size();
}
@SuppressWarnings("unchecked")
int compare(K key1, K key2)
{
return kComparator == null ? ((Comparable<K>)key1).compareTo(key2) : kComparator.compare(key1, key2);
}
/**
* 在节点中查找给定的键。
* 如果节点中存在给定的键,则返回一个SearchResult,
* 标识此次查找成功,给定的键在节点中的索引和给定的键关联的值;
* 这是一个二分查找算法,可以保证时间复杂度为O(log(t))。
* @param key - 给定的键值
* @return - 查找结果
*/
public SearchResult<V> searchKey(K key)
{
int low = 0;
int high = entrys.size() - 1;
int mid = 0;
while(low <= high)
{
mid = (low + high) / 2; // 先这么写吧,BTree实现中,l+h不可能溢出
Entry<K, V> entry = entrys.get(mid);
if(compare(entry.getKey(), key) == 0) // entrys.get(mid).getKey() == key
break;
else if(compare(entry.getKey(), key) > 0) // entrys.get(mid).getKey() > key
high = mid - 1;
else // entry.get(mid).getKey() < key
low = mid + 1;
}
boolean result = false;
int index = 0;
V value = null;
if(low <= high) // 说明查找成功
{
result = true;
index = mid; // index表示元素所在的位置
value = entrys.get(index).getValue();
}
else
{
result = false;
index = low; // index表示元素应该插入的位置
}
return new SearchResult<V>(result, index, value);
}
/**
* 将给定的项追加到节点的末尾,
* 你需要自己确保调用该方法之后,节点中的项还是
* 按照关键字以非降序存放。
* @param entry - 给定的项
*/
public void addEntry(Entry<K, V> entry)
{
entrys.add(entry);
}
/**
* 删除给定索引的entry
* 你需要自己保证给定的索引是合法的。
* @param index - 给定的索引
*/
public Entry<K, V> removeEntry(int index)
{
return entrys.remove(index);
}
/**
* 得到节点中给定索引的项。
* 你需要自己保证给定的索引是合法的。
* @param index - 给定的索引
* @return 节点中给定索引的项
*/
public Entry<K, V> entryAt(int index)
{
return entrys.get(index);
}
/**
* 如果节点中存在给定的键,则更新其关联的值。
* 否则插入。
* @param entry - 给定的项
* @return null,如果节点之前不存在给定的键,否则返回给定键之前关联的值
*/
public V putEntry(Entry<K, V> entry)
{
SearchResult<V> result = searchKey(entry.getKey());
if(result.isExist())
{
V oldValue = entrys.get(result.getIndex()).getValue();
entrys.get(result.getIndex()).setValue(entry.getValue());
return oldValue;
}
else
{
insertEntry(entry, result.getIndex());
return null;
}
}
/**
* 在该节点中插入给定的项,
* 该方法保证插入之后,其键值还是以非降序存放。
* 不过该方法的时间复杂度为O(t)。
* 注意:B树中不允许键值重复。
* @param entry - 给定的键值
* @return true,如果插入成功,false,如果插入失败
*/
public boolean insertEntry(Entry<K, V> entry)
{
SearchResult<V> result = searchKey(entry.getKey());
if(result.isExist())
return false;
else
{
insertEntry(entry, result.getIndex());
return true;
}
}
/**
* 在该节点中给定索引的位置插入给定的项,
* 你需要自己保证项插入了正确的位置。
* @param index - 给定的索引
*/
public void insertEntry(Entry<K, V> entry, int index)
{
/*
* 通过新建一个ArrayList来实现插入
* 要是有类似C中的reallocate就好了。
*/
List<Entry<K, V>> newEntrys = new ArrayList<Entry<K, V>>();
int i = 0;
// index = 0或者index = keys.size()都没有问题
for(; i < index; ++ i)
newEntrys.add(entrys.get(i));
newEntrys.add(entry);
for(; i < entrys.size(); ++ i)
newEntrys.add(entrys.get(i));
entrys.clear();
entrys = newEntrys;
}
/**
* 返回节点中给定索引的子节点。
* 你需要自己保证给定的索引是合法的。
* @param index - 给定的索引
* @return 给定索引对应的子节点
*/
public BTreeNode<K, V> childAt(int index)
{
if(isLeaf())
throw new UnsupportedOperationException("Leaf node doesn't have children.");
return children.get(index);
}
/**
* 将给定的子节点追加到该节点的末尾。
* @param child - 给定的子节点
*/
public void addChild(BTreeNode<K, V> child)
{
children.add(child);
}
/**
* 删除该节点中给定索引位置的子节点。
* 你需要自己保证给定的索引是合法的。
* @param index - 给定的索引
*/
public void removeChild(int index)
{
children.remove(index);
}
/**
* 将给定的子节点插入到该节点中给定索引
* 的位置。
* @param child - 给定的子节点
* @param index - 子节点带插入的位置
*/
public void insertChild(BTreeNode<K, V> child, int index)
{
List<BTreeNode<K, V>> newChildren = new ArrayList<BTreeNode<K, V>>();
int i = 0;
for(; i < index; ++ i)
newChildren.add(children.get(i));
newChildren.add(child);
for(; i < children.size(); ++ i)
newChildren.add(children.get(i));
children = newChildren;
}
}
把查询结果单独保存:
/**
* 在B树节点中搜索给定键值的返回结果。
* 该结果有两部分组成。第一部分表示此次查找是否成功,
* 如果查找成功,第二部分表示给定键值在B树节点中的位置,
* 如果查找失败,第二部分表示给定键值应该插入的位置。
*/
public class SearchResult<V>
{
private boolean exist;
private int index;
private V value;
public SearchResult(boolean exist, int index)
{
this.exist = exist;
this.index = index;
}
public SearchResult(boolean exist, int index, V value)
{
this(exist, index);
this.value = value;
}
public boolean isExist()
{
return exist;
}
public int getIndex()
{
return index;
}
public V getValue()
{
return value;
}
}下面进入真正的BTree类:
public class BTree<K, V>
{
private static Log logger = LogFactory.getLog(BTree.class);
private static final int DEFAULT_T = 2;
/** B树的根节点 */
private BTreeNode<K, V> root;
/** 根据B树的定义,B树的每个非根节点的关键字数n满足(t - 1) <= n <= (2t - 1) */
private int t = DEFAULT_T;
/** 非根节点中最小的键值数 */
private int minKeySize = t - 1;
/** 非根节点中最大的键值数 */
private int maxKeySize = 2*t - 1;
/** 键的比较函数对象 */
private Comparator<K> kComparator;
/**
* 构造一颗B树,键值采用采用自然排序方式
*/
public BTree()
{
root = new BTreeNode<K, V>();
root.setLeaf(true);
}
public BTree(int t)
{
this();
this.t = t;
minKeySize = t - 1;
maxKeySize = 2*t - 1;
}
/**
* 以给定的键值比较函数对象构造一颗B树。
*
* @param kComparator - 键值的比较函数对象
*/
public BTree(Comparator<K> kComparator)
{
root = new BTreeNode<K, V>(kComparator);
root.setLeaf(true);
this.kComparator = kComparator;
}
public BTree(Comparator<K> kComparator, int t)
{
this(kComparator);
this.t = t;
minKeySize = t - 1;
maxKeySize = 2*t - 1;
}
@SuppressWarnings("unchecked")
int compare(K key1, K key2)
{
return kComparator == null ? ((Comparable<K>)key1).compareTo(key2) : kComparator.compare(key1, key2);
}
/**
* 搜索给定的键。
*
* @param key - 给定的键值
* @return 键关联的值,如果存在,否则null
*/
public V search(K key)
{
return search(root, key);
}
/**
* 在以给定节点为根的子树中,递归搜索
* 给定的<code>key</code>
*
* @param node - 子树的根节点
* @param key - 给定的键值
* @return 键关联的值,如果存在,否则null
*/
private V search(BTreeNode<K, V> node, K key)
{
SearchResult<V> result = node.searchKey(key);
if(result.isExist())
return result.getValue();
else
{
if(node.isLeaf())
return null;
else
search(node.childAt(result.getIndex()), key);
}
return null;
}
/**
* 分裂一个满子节点<code>childNode</code>。
* <p/>
* 你需要自己保证给定的子节点是满节点。
*
* @param parentNode - 父节点
* @param childNode - 满子节点
* @param index - 满子节点在父节点中的索引
*/
private void splitNode(BTreeNode<K, V> parentNode, BTreeNode<K, V> childNode, int index)
{
assert childNode.size() == maxKeySize;
BTreeNode<K, V> siblingNode = new BTreeNode<K, V>(kComparator);
siblingNode.setLeaf(childNode.isLeaf());
// 将满子节点中索引为[t, 2t - 2]的(t - 1)个项插入新的节点中
for(int i = 0; i < minKeySize; ++ i)
siblingNode.addEntry(childNode.entryAt(t + i));
// 提取满子节点中的中间项,其索引为(t - 1)
Entry<K, V> entry = childNode.entryAt(t - 1);
// 删除满子节点中索引为[t - 1, 2t - 2]的t个项
for(int i = maxKeySize - 1; i >= t - 1; -- i)
childNode.removeEntry(i);
if(!childNode.isLeaf()) // 如果满子节点不是叶节点,则还需要处理其子节点
{
// 将满子节点中索引为[t, 2t - 1]的t个子节点插入新的节点中
for(int i = 0; i < minKeySize + 1; ++ i)
siblingNode.addChild(childNode.childAt(t + i));
// 删除满子节点中索引为[t, 2t - 1]的t个子节点
for(int i = maxKeySize; i >= t; -- i)
childNode.removeChild(i);
}
// 将entry插入父节点
parentNode.insertEntry(entry, index);
// 将新节点插入父节点
parentNode.insertChild(siblingNode, index + 1);
}
/**
* 在一个非满节点中插入给定的项。
*
* @param node - 非满节点
* @param entry - 给定的项
* @return true,如果B树中不存在给定的项,否则false
*/
private boolean insertNotFull(BTreeNode<K, V> node, Entry<K, V> entry)
{
assert node.size() < maxKeySize;
if(node.isLeaf()) // 如果是叶子节点,直接插入
return node.insertEntry(entry);
else
{
/* 找到entry在给定节点应该插入的位置,那么entry应该插入
* 该位置对应的子树中
*/
SearchResult<V> result = node.searchKey(entry.getKey());
// 如果存在,则直接返回失败
if(result.isExist())
return false;
BTreeNode<K, V> childNode = node.childAt(result.getIndex());
if(childNode.size() == 2*t - 1) // 如果子节点是满节点
{
// 则先分裂
splitNode(node, childNode, result.getIndex());
/* 如果给定entry的键大于分裂之后新生成项的键,则需要插入该新项的右边,
* 否则左边。
*/
if(compare(entry.getKey(), node.entryAt(result.getIndex()).getKey()) > 0)
childNode = node.childAt(result.getIndex() + 1);
}
return insertNotFull(childNode, entry);
}
}
/**
* 在B树中插入给定的键值对。
*
* @param key - 键
* @param value - 值
*/
public boolean insert(K key, V value)
{
if(root.size() == maxKeySize) // 如果根节点满了,则B树长高
{
BTreeNode<K, V> newRoot = new BTreeNode<K, V>(kComparator);
newRoot.setLeaf(false);
newRoot.addChild(root);
splitNode(newRoot, root, 0);
root = newRoot;
}
return insertNotFull(root, new Entry<K, V>(key, value));
}
/**
* 如果存在给定的键,则更新键关联的值,
* 否则插入给定的项。
*
* @param node - 非满节点
* @param entry - 给定的项
* @return true,如果B树中不存在给定的项,否则false
*/
private V putNotFull(BTreeNode<K, V> node, Entry<K, V> entry)
{
assert node.size() < maxKeySize;
if(node.isLeaf()) // 如果是叶子节点,直接插入
return node.putEntry(entry);
else
{
/* 找到entry在给定节点应该插入的位置,那么entry应该插入
* 该位置对应的子树中
*/
SearchResult<V> result = node.searchKey(entry.getKey());
// 如果存在,则更新
if(result.isExist())
return node.putEntry(entry);
BTreeNode<K, V> childNode = node.childAt(result.getIndex());
if(childNode.size() == 2*t - 1) // 如果子节点是满节点
{
// 则先分裂
splitNode(node, childNode, result.getIndex());
/* 如果给定entry的键大于分裂之后新生成项的键,则需要插入该新项的右边,
* 否则左边。
*/
if(compare(entry.getKey(), node.entryAt(result.getIndex()).getKey()) > 0)
childNode = node.childAt(result.getIndex() + 1);
}
return putNotFull(childNode, entry);
}
}
/**
* 如果B树中存在给定的键,则更新值。
* 否则插入。
*
* @param key - 键
* @param value - 值
* @return 如果B树中存在给定的键,则返回之前的值,否则null
*/
public V put(K key, V value)
{
if(root.size() == maxKeySize) // 如果根节点满了,则B树长高
{
BTreeNode<K, V> newRoot = new BTreeNode<K, V>(kComparator);
newRoot.setLeaf(false);
newRoot.addChild(root);
splitNode(newRoot, root, 0);
root = newRoot;
}
return putNotFull(root, new Entry<K, V>(key, value));
}
/**
* 从B树中删除一个与给定键关联的项。
*
* @param key - 给定的键
* @return 如果B树中存在给定键关联的项,则返回删除的项,否则null
*/
public Entry<K, V> delete(K key)
{
return delete(root, key);
}
/**
* 从以给定<code>node</code>为根的子树中删除与给定键关联的项。
* <p/>
* 删除的实现思想请参考《算法导论》第二版的第18章。
*
* @param node - 给定的节点
* @param key - 给定的键
* @return 如果B树中存在给定键关联的项,则返回删除的项,否则null
*/
private Entry<K, V> delete(BTreeNode<K, V> node, K key)
{
// 该过程需要保证,对非根节点执行删除操作时,其关键字个数至少为t。
assert node.size() >= t || node == root;
SearchResult<V> result = node.searchKey(key);
/*
* 因为这是查找成功的情况,0 <= result.getIndex() <= (node.size() - 1),
* 因此(result.getIndex() + 1)不会溢出。
*/
if(result.isExist())
{
// 1.如果关键字在节点node中,并且是叶节点,则直接删除。
if(node.isLeaf())
return node.removeEntry(result.getIndex());
else
{
// 2.a 如果节点node中前于key的子节点包含至少t个项
BTreeNode<K, V> leftChildNode = node.childAt(result.getIndex());
if(leftChildNode.size() >= t)
{
// 使用leftChildNode中的最后一个项代替node中需要删除的项
node.removeEntry(result.getIndex());
node.insertEntry(leftChildNode.entryAt(leftChildNode.size() - 1), result.getIndex());
// 递归删除左子节点中的最后一个项
return delete(leftChildNode, leftChildNode.entryAt(leftChildNode.size() - 1).getKey());
}
else
{
// 2.b 如果节点node中后于key的子节点包含至少t个关键字
BTreeNode<K, V> rightChildNode = node.childAt(result.getIndex() + 1);
if(rightChildNode.size() >= t)
{
// 使用rightChildNode中的第一个项代替node中需要删除的项
node.removeEntry(result.getIndex());
node.insertEntry(rightChildNode.entryAt(0), result.getIndex());
// 递归删除右子节点中的第一个项
return delete(rightChildNode, rightChildNode.entryAt(0).getKey());
}
else // 2.c 前于key和后于key的子节点都只包含t-1个项
{
Entry<K, V> deletedEntry = node.removeEntry(result.getIndex());
node.removeChild(result.getIndex() + 1);
// 将node中与key关联的项和rightChildNode中的项合并进leftChildNode
leftChildNode.addEntry(deletedEntry);
for(int i = 0; i < rightChildNode.size(); ++ i)
leftChildNode.addEntry(rightChildNode.entryAt(i));
// 将rightChildNode中的子节点合并进leftChildNode,如果有的话
if(!rightChildNode.isLeaf())
{
for(int i = 0; i <= rightChildNode.size(); ++ i)
leftChildNode.addChild(rightChildNode.childAt(i));
}
return delete(leftChildNode, key);
}
}
}
}
else
{
/*
* 因为这是查找失败的情况,0 <= result.getIndex() <= node.size(),
* 因此(result.getIndex() + 1)会溢出。
*/
if(node.isLeaf()) // 如果关键字不在节点node中,并且是叶节点,则什么都不做,因为该关键字不在该B树中
{
logger.info("The key: " + key + " isn't in this BTree.");
return null;
}
BTreeNode<K, V> childNode = node.childAt(result.getIndex());
if(childNode.size() >= t) // // 如果子节点有不少于t个项,则递归删除
return delete(childNode, key);
else // 3
{
// 先查找右边的兄弟节点
BTreeNode<K, V> siblingNode = null;
int siblingIndex = -1;
if(result.getIndex() < node.size()) // 存在右兄弟节点
{
if(node.childAt(result.getIndex() + 1).size() >= t)
{
siblingNode = node.childAt(result.getIndex() + 1);
siblingIndex = result.getIndex() + 1;
}
}
// 如果右边的兄弟节点不符合条件,则试试左边的兄弟节点
if(siblingNode == null)
{
if(result.getIndex() > 0) // 存在左兄弟节点
{
if(node.childAt(result.getIndex() - 1).size() >= t)
{
siblingNode = node.childAt(result.getIndex() - 1);
siblingIndex = result.getIndex() - 1;
}
}
}
// 3.a 有一个相邻兄弟节点至少包含t个项
if(siblingNode != null)
{
if(siblingIndex < result.getIndex()) // 左兄弟节点满足条件
{
childNode.insertEntry(node.entryAt(siblingIndex), 0);
node.removeEntry(siblingIndex);
node.insertEntry(siblingNode.entryAt(siblingNode.size() - 1), siblingIndex);
siblingNode.removeEntry(siblingNode.size() - 1);
// 将左兄弟节点的最后一个孩子移到childNode
if(!siblingNode.isLeaf())
{
childNode.insertChild(siblingNode.childAt(siblingNode.size()), 0);
siblingNode.removeChild(siblingNode.size());
}
}
else // 右兄弟节点满足条件
{
childNode.insertEntry(node.entryAt(result.getIndex()), childNode.size() - 1);
node.removeEntry(result.getIndex());
node.insertEntry(siblingNode.entryAt(0), result.getIndex());
siblingNode.removeEntry(0);
// 将右兄弟节点的第一个孩子移到childNode
// childNode.insertChild(siblingNode.childAt(0), childNode.size() + 1);
if(!siblingNode.isLeaf())
{
childNode.addChild(siblingNode.childAt(0));
siblingNode.removeChild(0);
}
}
return delete(childNode, key);
}
else // 3.b 如果其相邻左右节点都包含t-1个项
{
if(result.getIndex() < node.size()) // 存在右兄弟,直接在后面追加
{
BTreeNode<K, V> rightSiblingNode = node.childAt(result.getIndex() + 1);
childNode.addEntry(node.entryAt(result.getIndex()));
node.removeEntry(result.getIndex());
node.removeChild(result.getIndex() + 1);
for(int i = 0; i < rightSiblingNode.size(); ++ i)
childNode.addEntry(rightSiblingNode.entryAt(i));
if(!rightSiblingNode.isLeaf())
{
for(int i = 0; i <= rightSiblingNode.size(); ++ i)
childNode.addChild(rightSiblingNode.childAt(i));
}
}
else // 存在左节点,在前面插入
{
BTreeNode<K, V> leftSiblingNode = node.childAt(result.getIndex() - 1);
childNode.insertEntry(node.entryAt(result.getIndex() - 1), 0);
node.removeEntry(result.getIndex() - 1);
node.removeChild(result.getIndex() - 1);
for(int i = leftSiblingNode.size() - 1; i >= 0; -- i)
childNode.insertEntry(leftSiblingNode.entryAt(i), 0);
if(!leftSiblingNode.isLeaf())
{
for(int i = leftSiblingNode.size(); i >= 0; -- i)
childNode.insertChild(leftSiblingNode.childAt(i), 0);
}
}
// 如果node是root并且node不包含任何项了
if(node == root && node.size() == 0)
root = childNode;
return delete(childNode, key);
}
}
}
}
/**
* 一个简单的层次遍历B树实现,用于输出B树。
*/
public void output()
{
Queue<BTreeNode<K, V>> queue = new LinkedList<BTreeNode<K, V>>();
queue.offer(root);
while(!queue.isEmpty())
{
BTreeNode<K, V> node = queue.poll();
for(int i = 0; i < node.size(); ++ i)
System.out.print(node.entryAt(i) + " ");
System.out.println();
if(!node.isLeaf())
{
for(int i = 0; i <= node.size(); ++ i)
queue.offer(node.childAt(i));
}
}
}
}
测试类:
public class Test {
public static void main(String[] args)
{
Random random = new Random();
BTree<Integer, Integer> btree = new BTree<Integer, Integer>(3);
List<Integer> save = new ArrayList<Integer>();
for(int i = 0; i < 10; ++ i)
{
int r = random.nextInt(100);
save.add(r);
System.out.println(r);
btree.insert(r, r);
}
System.out.println("----------------------");
btree.output();
System.out.println("----------------------");
btree.delete(save.get(0));
btree.output();
}
}
测试结果:
65
30
15
86
54
43
30
8
81
65
----------------------
54:54
8:8 15:15 30:30 43:43
65:65 81:81 86:86
----------------------
54:54
8:8 15:15 30:30 43:43
81:81 86:86 五、B+树
5.1 什么是B+树?
B+树是在B树上的扩展,查询性能更优秀。
一个m阶的B+树具有如下几个特征:
- 有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都在叶子节点。
- 所有叶子结点中包含全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。

上面就是一个B+树,首先父节点的元素都出现在了子节点中,且是子节点中最大(或最小)的元素,根节点中最大元素等同于整棵树的最大元素,在删除新增元素时这个都不会变,保证最大元素在根节点;因为父节点的元素都出现在了子节点中,所以所有叶子节点包含了全部的元素信息。叶子节点是通过指针连接的,形成了有序链表,因此B+树可以支持范围查询。
5.2 B+树和B树区别
- B+树相同情况下比B树需要的IO次数更少
- B+树的查询必须最终查询到子节点,B树只要找到元素即可,不管是不是在叶子节点
- B+树支持范围查找,B树是一次一次遍历
(ps:还有一种B*树的,B*树是在B+树基础上,为非叶子结点也增加链表指针)
六、图
6.1 什么是"图"?
图是一种网络结构的抽象模型。
举个非常常见的例子:
我们每天在使用百度、高德地图进行导航时,城市的地图就是一种图的结构。我们使用QQ、微信、Twitter、Facebook等社交软件,我们的好友关系网也是一种图的结构。不仅如此,我们还可以使用图来表示道路、航班以及通信。

6.2 图的相关术语
一个图由 G = (V,E)组成:
- V:一组顶点
- E:一组边,连接V中的顶点
顶点:图最基本的单元,也就是图中的节点。
边:顶点之间的关联关系,被称为边。
相邻顶点:由一条边连接在一起的顶点,被称为相邻顶点。
度:一个顶点包含的相邻顶点的数量,被称为度。
权重和带权图:
有些图中,每一条边并不是完全等同的。如在地铁线路组成的图中,A站到B站的距离是3km,B站到C站的距离是5km,则该数值便是图的权重,而这种图,则被称为带权图。

有向图:
如果图中节点之间的边线是单向的,则被称为有向图。

无向图:
如果图中节点之间的边线是双向的,或者没有一个明确的指向,则被称为无向图。

七、 Trie树 —— 字典树
trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie 的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
7.1 基本性质
1、根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2、从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3、每个节点的所有子节点包含的字符都不相同。

一般而言,应该是用一个点来表示一个字符,为了更好的说明,所以用边来描述字符。
从根结点到树上某一结点的路径就代表了一个字符串。举个例子, 1→2→6表示的就是字符串 aba。
再比如,1→4→8构成的字符串是ca,那么如果在往下拓展的话,我们是不是有 caa,cab,那么他们都会经过1→4→8,这些路径,说明他们是有一段公共的前缀,这个前缀的内容就是ca,说道这里,我们就知道字典树利用的就是字符串的前缀来解决问题。
7.2 应用场景
在搜索引擎中关键词提示,引擎会自动弹出匹配关键词的下拉框。

那么应该如何利用一种高效的数据结构存储呢,这里就符合字典树的性质,所以可以利用字典树来构造特定的数据,达到一种更加快速检索的效果。
字符串检索
事先将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率,可以举例子说明情况👇
- 1000万字符串,其中有些是重复的,需要把重复的全部去掉,保留没有重复的字符串。
- 给出N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
词频统计
给定很长的一个串,统计频数出现次数最多情况,举个例子👇
- 有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
- 一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀,所以可以利用这个特点来解决一些前缀问题。
非要举个例子的话,有个例子👇
- 给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少?
7.3 应用例子
词典中最长的单词
给出一个字符串数组words组成的一本英语词典。从中找出最长的一个单词,该单词是由words词典中其他单词逐步添加一个字母组成。若其中有多个可行的答案,则返回答案中字典序最小的单词。若无答案,则返回空字符串。
示例 1:
输入:
words = ["w","wo","wor","worl", "world"]
输出:"world"
解释:
单词"world"可由"w", "wo", "wor", 和 "worl"添加一个字母组成。
复制代码示例 2:
输入:
words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
输出:"apple"
解释:
"apply"和"apple"都能由词典中的单词组成。但是"apple"的字典序小于"apply"。解法构造字典树。
7.4 构造字典树
public class TrieTree {
class TrieNode{
public TrieNode[] subNode;
public int count;//该节点的子节点个数
public boolean isWord;//单词标记位
public TrieNode() {
this.count = 0;
this.isWord = false;
this.subNode = new TrieNode[26];//只包含小写字母a-z
}
}
public TrieNode root;
public TrieTree() {
root = new TrieNode();
}
public boolean search(String word) {
TrieNode curNode = root;
int index;
for(int i = 0; i < word.length(); i++) {
index = word.charAt(i)-'a';
if(curNode.subNode[index]!= null) {
curNode = curNode.subNode[index];
}else{
return false;
}
}
return curNode.isWord;
}
public void insert(String word) {
if(search(word)) {
System.out.println("The word already exists.");
return;
}
TrieNode node = root;
int index;
for(int i = 0; i < word.length(); i++) {
index = word.charAt(i) - 'a';
if(node.subNode[index]==null) {
node.subNode[index]= new TrieNode();
}
node.count++;
node = node.subNode[index];
}
node.isWord = true;
}
public void delete(String word) {
if(!search(word)) {
System.out.println("No such word.");
return;
}
TrieNode node = root;
LinkedList<Integer> indexList = new LinkedList();
LinkedList<TrieNode> nodeList = new LinkedList();
int index;
for(int i = 0; i < word.length(); i++) {
index = word.charAt(i) - 'a';
indexList.add(index);
nodeList.add(node);
node = node.subNode[index];
}
for(int i = word.length() - 1; i >= 0; i--) {
node = nodeList.pollLast();
index = indexList.pollLast();
if(node.subNode[index].subNode == null) {
if(i != word.length() - 1) {
if(node.subNode[index].isWord == true) {//如果前缀节点中有单词标记位,那么不再继续删除
return;
}
}
node.subNode[index] = null;
node.count--;
}
if(i == word.length()-1) {
if(node.subNode[index].subNode != null) {
node.subNode[index].isWord = false;
return;
}
}
}
}
public static void main(String[] args) {
TrieTree myTrieTree = new TrieTree();
String[] words = {"hello","face","hi","hell","why"};
//插入字符串
for(String word : words)
myTrieTree.insert(word);
//插入重复字符串
myTrieTree.insert("hello");
//删除字符串
myTrieTree.delete("hell");
//重复删除字符串
myTrieTree.delete("hell");
myTrieTree.delete("hi");
//查询字符串,找到为true,未找到为false
System.out.println(myTrieTree.search("hello"));
System.out.println(myTrieTree.search("hi"));
System.out.println(myTrieTree.search("hell"));
}
}
八、其他
8.1 B树和红黑树的区别
B树与红黑树最大的不同在于,B树的结点可以有许多子女,从几个到几千个,红黑树最多只有两个分叉。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!