岛屿的个数12 · Number of Islands12
[抄题]:
给一个01矩阵,求不同的岛屿的个数。
0代表海,1代表岛,如果两个1相邻,那么这两个1属于同一个岛。我们只考虑上下左右为相邻。
[
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 1]
][暴力解法]:
时间分析:
空间分析:
[思维问题]:
[一句话思路]:
找到一个岛,用dfs沉没一片岛。
[输入量]:空: 正常情况:特大:特小:程序里处理到的特殊情况:异常情况(不合法不合理的输入):
[画图]:
[一刷]:
- for (i = 0; i < n; i++)留头去尾,保持n个数,真要理解
- DFS的循环退出条件中,边界条件在前 作为前提 先控制,题目自身的循环条件后控制
- 数组的length不要括号,别顺手敲成习惯了
[二刷]:
[三刷]:
[四刷]:
[五刷]:
[五分钟肉眼debug的结果]:
[总结]:
[复杂度]:Time complexity: O(m*n)每个点触及1次 Space complexity: O(m* n)
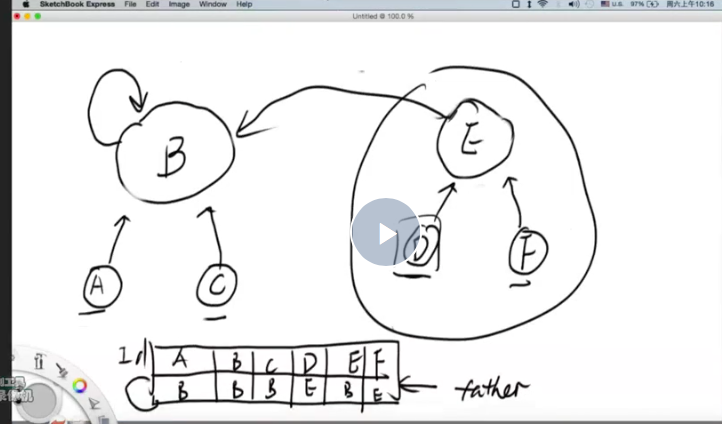
一般情况下每个点都要找,为n
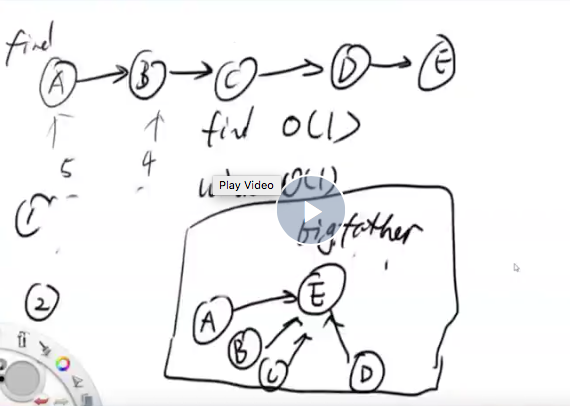
压缩情况下仅保存终点,为1 。
本来都是爷爷传给爸爸,现在爸爸直接指向祖宗,不用再爷爷传给爸爸了。
[英文数据结构或算法,为什么不用别的数据结构或算法]:
DFS
[关键代码]:

if (i < 0 || j< 0 || i >= n || j >= m || grid[i][j] != true) {//qiatouquwei,youxianhou
return ;
}
//dfs
grid[i][j] = false;
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
[其他解法]:
bfs,union find
[Follow Up]:
[LC给出的题目变变变]:
[代码风格] :

public class Solution {
private int n;
private int m;
public int numIslands(char[][] grid) {
int count = 0;
n = grid.length;
if (n == 0) return 0;
m = grid[0].length;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++)
if (grid[i][j] == '1') {
DFSMarking(grid, i, j);
++count;
}
}
return count;
}
private void DFSMarking(char[][] grid, int i, int j) {
if (i < 0 || j < 0 || i >= n || j >= m || grid[i][j] != '1') return;
grid[i][j] = '0';
DFSMarking(grid, i + 1, j);
DFSMarking(grid, i - 1, j);
DFSMarking(grid, i, j + 1);
DFSMarking(grid, i, j - 1);
}
}
[抄题]:
给定 n,m,分别代表一个2D矩阵的行数和列数,同时,给定一个大小为 k 的二元数组A。起初,2D矩阵的行数和列数均为 0,即该矩阵中只有海洋。二元数组有 k 个运算符,每个运算符有 2 个整数 A[i].x, A[i].y,你可通过改变矩阵网格中的A[i].x],[A[i].y] 来将其由海洋改为岛屿。请在每次运算后,返回矩阵中岛屿的数量。
给定 n = 3, m = 3, 二元数组 A = [(0,0),(0,1),(2,2),(2,1)].
返回 [1,1,2,2].
[暴力解法]:
时间分析:
空间分析:
[思维问题]:
(单一责任原则)用一个函数功能处理完所有数据,再用下一个函数功能处理所有数据。
需要把二维坐标转换为一维节点,才能用并查集,这一步没想到。
用island[x][y] 标记某小岛是否出现过,若第一次出现则标记为1。棋盘形的题可以用数组标记1表示某元素是否出现过,以前做过但是没总结,忘了。
[一句话思路]:
用union find,不重复地添加其周围的岛。
[输入量]:空: 正常情况:特大:特小:程序里处理到的特殊情况:异常情况(不合法不合理的输入):
[画图]:
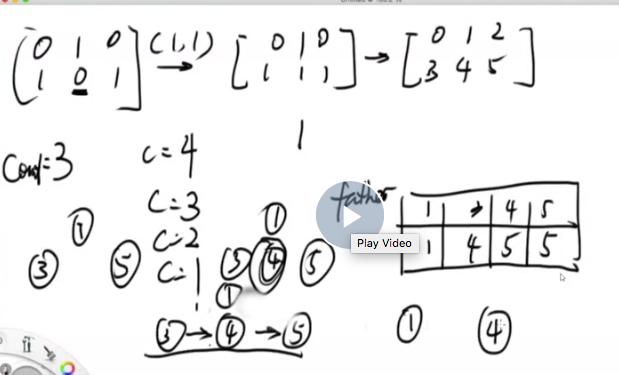
应该用big father合并,防止节点从属关系的丢失
[一刷]:
- UnionFind中的UnionFind方法的目的是预处理,把所有的二维节点生成一维id,放在hashmap中等待查询。需要把二维坐标转换为一维节点,才能用并查集,这一步没有理解其意义。
[二刷]:
[三刷]:
[四刷]:
[五刷]:
[五分钟肉眼debug的结果]:
[总结]:
棋盘形的题可以用数组标记1表示某元素是否出现过,如果不是岛,变成岛并且统计四周的扩展。
[复杂度]:Time complexity: O(最坏m*n每个点都是*4*1) Space complexity: O(m*n)
[英文数据结构或算法,为什么不用别的数据结构或算法]:
- class是关键字 一般新定义的类要用,Class是一个单独的包
- uf.compressed_find(id); 由于系统import的包中没有需要的类,就自己写了个unifind class,新方法也是新类自带的,系统没有,所以要指明所属的类。
[关键模板化代码]:

for (int j = 0; j < 4; j++) {
int nx = x + dx[j];
int ny = y + dy[j];
if (0 <= nx && nx < n && 0 <= ny && ny < m
&& islands[nx][ny] == 1) {
[其他解法]:
[Follow Up]:
[LC给出的题目变变变]:
721. Accounts Merge 邮件合并
[代码风格] :

/**
* Definition for a point.
* class Point {
* int x;
* int y;
* Point() { x = 0; y = 0; }
* Point(int a, int b) { x = a; y = b; }
* }
*/
public class Solution {
/*
* @param n: An integer
* @param m: An integer
* @param operators: an array of point
* @return: an integer array
*/
//covertToID
public int covertToID (int x, int y, int m) {
return x * m + y;
}
class UnionFind {//xiaoxie
HashMap<Integer, Integer> father = new HashMap<>();
//find, pre-storage for m * n
UnionFind(int n, int m) {//n first m second
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int id = covertToID(i, j, m);
father.put(id, id);
}
}
}
//compressed_find
int compressed_find (int x) {
//find ultimate parent
int parent = father.get(x);
while (parent != father.get(parent)) {
parent = father.get(parent);
}
//covert the grandfather to ultimate parent
int temp = -1;
int fa = x;
while (fa != father.get(fa)) {
temp = father.get(fa);
father.put(fa, parent);
fa = temp;
}
return parent;
}
//union
void union(int x, int y) {
int fa_x = compressed_find(x);
int fa_y = compressed_find(y);
if (fa_x != fa_y) {
father.put(fa_x, fa_y);
}
}
}
public List<Integer> numIslands2(int n, int m, Point[] operators) {
List<Integer> ans = new ArrayList<Integer>();
//corner case
if (operators == null) {
return ans;
}
int[] dx = {0, 1, 0, -1};
int[] dy = {1, 0, -1, 0};
int count = 0;
int[][] islands = new int[n][m];
UnionFind uf = new UnionFind(n, m);
//for lop
for (int i = 0; i < operators.length; i++) {
//get an island from list
int x = operators[i].x;
int y = operators[i].y;
//check whether is not island before, but is island now
if (islands[x][y] != 1) {
int id = covertToID(x, y, m);
islands[x][y] = 1;
count++;
//expand to check
for (int j = 0; j < 4; j++) {
int nx = x + dx[j];
int ny = y + dy[j];
int nid = covertToID(nx, ny, m);
if (0 <= nx && nx < n && 0 <= ny && ny < m
&& islands[nx][ny] == 1) {
int fa = uf.compressed_find(id);//new obeject's method
int nfa = uf.compressed_find(nid);
if (fa != nfa) {
uf.union(id, nid);
count--;
}
}
}
}
ans.add(count);
}
return ans;
}
}
[抄题]:
A 2d grid map of m rows and n columns is initially filled with water. We may perform an addLand operation which turns the water at position (row, col) into a land. Given a list of positions to operate, count the number of islands after each addLand operation. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example:
Input: m = 3, n = 3, positions = [[0,0], [0,1], [1,2], [2,1]] Output: [1,1,2,3]
加点,返回岛屿个数
[暴力解法]:
时间分析:
空间分析:
[优化后]:
时间分析:
空间分析:
[奇葩输出条件]:
[奇葩corner case]:
向四周添加的时候,可能会出现x y 超出范围或者之前没有岛屿的情况,要注意
[思维问题]:
[英文数据结构或算法,为什么不用别的数据结构或算法]:
[一句话思路]:
roots[root] = root; 靠一个id数组不断合并,每次合并都返回count[输入量]:空: 正常情况:特大:特小:程序里处理到的特殊情况:异常情况(不合法不合理的输入):
[画图]:

[一刷]:
- m行 n列,x表示行数 不超过m,y表示列数 不超过n
[二刷]:
find函数,不管是否用路径压缩,都用的是while循环,表示从x结点搜索到祖先结点所经过的结点都指向该祖先结点
public int find (int id, int[] roots) {
while (id != roots[id])
id = roots[roots[id]];
return id;
}
[三刷]:
[四刷]:
[五刷]:
[五分钟肉眼debug的结果]:
[总结]:
简化版的精髓就是:由root找next_id,由next_id找real_root(三连击),然后一言不合就合并。
[复杂度]:Time complexity: O(n) Space complexity: O(n)
[算法思想:迭代/递归/分治/贪心]:
[关键模板化代码]:
[其他解法]:
[Follow Up]:
[LC给出的题目变变变]:
[代码风格] :
[是否头一次写此类driver funcion的代码] :

// package whatever; // don't place package name!
import java.io.*;
import java.util.ArrayList;
import java.util.Arrays;
import java.lang.*;
class MyCode {
public static void main (String[] args) {
int [][]positions = {{0, 0},{0, 1},{1, 2},{2, 1}};
int m = 3, n = 3;
Solution rst = new Solution();
System.out.println(rst.numIslands2(m, n, positions));
}
}
class Solution {
int[][] dirs = {{0, 1},{0, -1},{1, 0},{-1, 0}};
public ArrayList<Integer> numIslands2(int m, int n, int[][] positions) {
//ini
int count = 0;
int[] roots = new int[m * n];
ArrayList<Integer> result = new ArrayList<Integer>();
Arrays.fill(roots, -1);
//cc
if (m <= 0 || n <= 0 || positions == null) return result;
//one island
for (int[] pos : positions) {
int root = n * pos[0] + pos[1];
roots[root] = root;
count++;
for (int[] dir : dirs) {
int nx = pos[0] + dir[0];
int ny = pos[1] + dir[1];
int next_id = nx * n + ny;
if (nx < 0 || nx >= m || ny < 0 || ny >= n || roots[next_id] == -1) continue;//?
int real_root = find(next_id, roots);//find next
if(real_root != root) {
roots[root] = real_root;
root = real_root;
count--;
}
}
result.add(count);
}
return result;
}
public int find (int id, int[] roots) {
while (id != roots[id])
id = roots[roots[id]];
return id;
}
}
import java.util.*;
import java.lang.*;
[台词]:
for this problem we have to do it with UnionFind, since this is a dynamic process to add all the island, and we need to return the number of islands during the process.
if we still use DFS (sinking method), then for every new island, we need to do the DFS again (O(mn)), as if we never had any information before.
but if we use UionFind, we could optimize the process to O(1), because we already stored the information about already existing islands.
real_root不同,但是可以合并成为同一组。
Then when we merge two cells belong to previously separated components, count—.
x coordinate




