53. Maximum Subarray最大求和子数组12 3（dp）

［抄题］：

Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.

 

方法一：贪心算法greedy

［一句话思路］：

每次都取最大值，sum-max-sum。

［画图］：

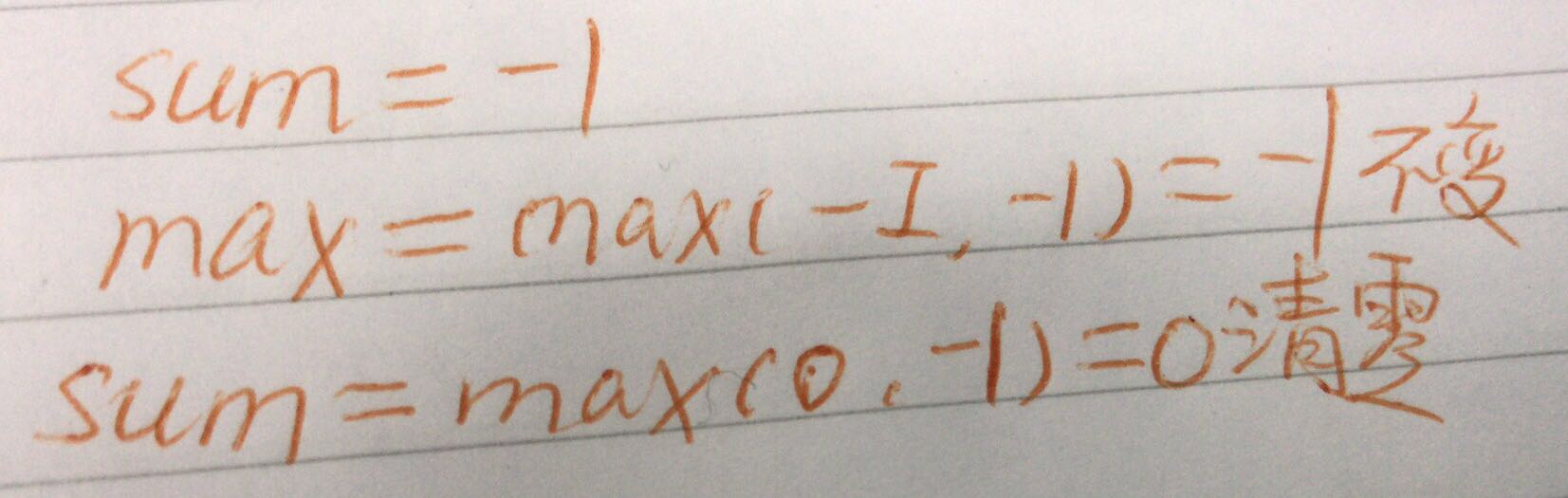
［一刷］：

［总结］：

就是背吧。

［复杂度］：

n/1

［英文数据结构］：

Range Queries

［其他解法］：

preflix sum

［题目变变变］：

minimum Subarray最小求和子数组。＊（－1）后变成copy[i]，求最大，再return（－1）＊copy[i]。

最大

 

public class Solution {
    /*
     * @param nums: a list of integers
     * @return: A integer indicate the sum of minimum subarray
     */
    public int minSubArray(List<Integer> nums) {
        // write your code here
        int size = nums.size();
        int[] left_min = new int[size];
        int[] copy = new int[size];
        /*Get negative copy*/
        for(int i = 0; i < size; i++){
            copy[i] = -1 * nums.get(i);
        }
        int max = Integer.MIN_VALUE;
        int sum = 0;
        int minSum = 0;
        
       for(int i = 0; i < size; i++){
            sum += copy[i];
            max = Math.max(max, sum - minSum);
            minSum = Math.min(sum, minSum);
        }
        return -1 * max;
    }
}

 

方法二：preflix sum

［一句话思路］：

［画图］：

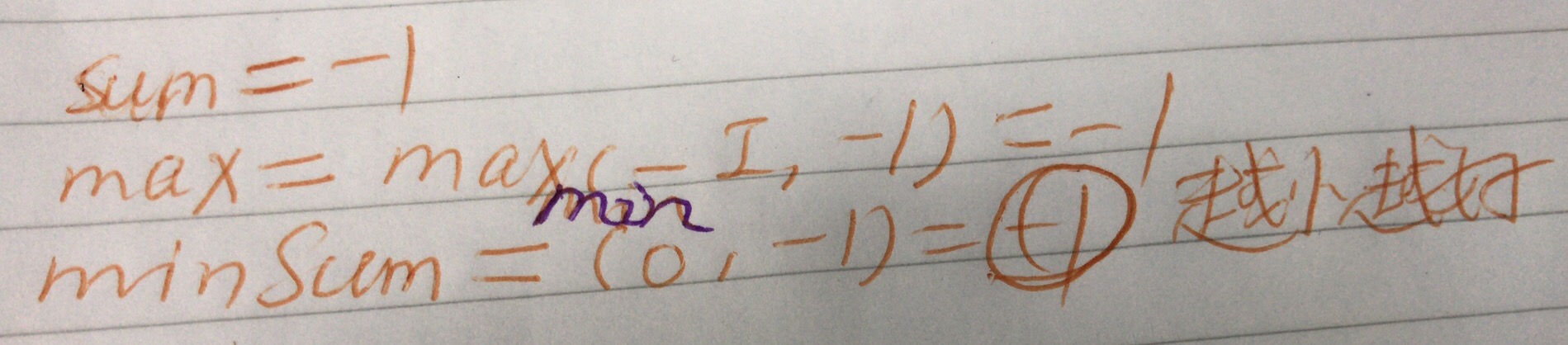
［一刷］：

minSum = Math.min(minSum, sum);为了使得连续和最大，Sum[j] 确定的情况下，Sum[i - 1]的值越小越好．

［总结］：

 也是sum-max-sum，注意minSum要取最小值。

［复杂度］：n/1

［英文数据结构］：

［其他解法］：

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 0 || nums == null) {
            return -1;
        }
        
        int sum = 0;
        int minSum = 0;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            max = Math.max(max, sum - minSum);
            minSum = Math.min(minSum, sum);
        }
        
        return max;
    }
}

 ［题目变变变］：

 

2

［抄题］：

 给定一个整数数组，找出两个 不重叠 子数组使得它们的和最大。每个子数组的数字在数组中的位置应该是连续的，返回最大的和。给出数组 [1, 3, -1, 2, -1, 2]
这两个子数组分别为 [1, 3] 和 [2, -1, 2] 或者 [1, 3, -1, 2] 和 [2]，它们的最大和都是 7。

［思维问题］：

以为因为两个数组不连续，不能用连续枚举。但由于是subarray所以可以。

［一句话思路］：

枚举：看哪个left[i] + right[i + 1]可以达到max

［画图］：

 

［一刷］：

1. 用preflix sum，变量都能复用：再初始化就行。
2. 最后枚举的时候不要用二元运算符，复用max就行了。
3. 链表长度函数是.size，不是.sizeof
4. for循环中的int i是局部变量，要重复定义
5.  for (int i = size - 1; i >= 0; i--) , 逆向时0也要取
6. 不要妄想把隔着的几个负数挑出来，结果对了就行。最后的max是负数也得认，所以初始化max = Integer.MIN_VALUE;
   

［总结］：

两个量都在变，还有位置关系时，用两个数组表示。

［复杂度］：

n/1

［英文数据结构］：

［其他解法］：

［题目变变变］：

 

思路：左右的max分别存一个数组，然后用  max = Math.max(max, left[i] + right[i + 1]);。

这个题的思路是，因为 两个subarray 一定不重叠

所以必定存在一条分割线

分开这两个 subarrays

所以 最后的部分里：

  max = Integer.MIN_VALUE;

        for(int i = 0; i < size - 1; i++){

            max = Math.max(max, left[i] + right[i + 1]);

        }

        return max;

这里是在枚举 这条分割线的位置

然后 left[] 和 right[] 里分别存的是，某个位置往左的 maximum subarray 和往右的 maximum subarray。

public class Solution {
    /*
     * @param nums: A list of integers
     * @return: An integer denotes the sum of max two non-overlapping subarrays
     */
    public int maxTwoSubArrays(List<Integer> nums) {
        // write your code here
        int size = nums.size();
        int[] left = new int [size];
        int[] right = new int [size];
        
        //put in the left, using perflix sum
        int sum = 0;
        int minSum = 0;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < size; i++) {
            sum += nums.get(i);
            max = Math.max(max, sum - minSum);
            minSum = Math.min(minSum, sum);
            
            left[i] = max;
        }
        
        //put in the right, using perflix sum
        sum = 0;
        minSum = 0;
        max = Integer.MIN_VALUE;
        for (int i = size - 1; i >= 0; i--) {//0也要取
            sum += nums.get(i);
            max = Math.max(max, sum - minSum);
            minSum = Math.min(minSum, sum);
            
            right[i] = max;
        }
        
        //for the result
        max = Integer.MIN_VALUE;
        for (int i = 0; i < size - 1; i++) {
            max = Math.max(max, left[i] + right[i + 1]);
        }
        
        return max;
    }
}