215. Kth Largest Element in an Array(QuickSort)
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
For example,
Given [3,2,1,5,6,4] and k = 2, return 5.
[一句话思路]:快速选择:先利用pivot进行两侧的排序,再选一侧递归查找。
[一刷]:
- Kth函数中要调用一次qs函数. qs函数要写成private int, 所有变量都要重新声明类型。{调用qs},{qs}要分开写。
- divide的过程要一直做,所以都用while(i < j)的大循环包起来,一直在pivot两侧找,找到后交换一次即可
[二刷]:
- 忘记写corner case了。。
- 不是length,是nums.length。nums.length是数组长度,nums.length-1是最后一位
- 不用给声明的参数制定具体数,调用时才指定
[总结]:两根指针,联想两个小人。
[复杂度]:
快选,每次选一部分,扔掉另一部分,所以是O(N)
假设每次扔掉一半.
(2^k=N)
T(N) =n +n/2+n/4+n/8+n/2^k = n*(1-2^-k)/(1-2^-1) =2N
[英文数据结构]:array
[其他解法]:
[题目变变变]:median, Kth in two array's combination
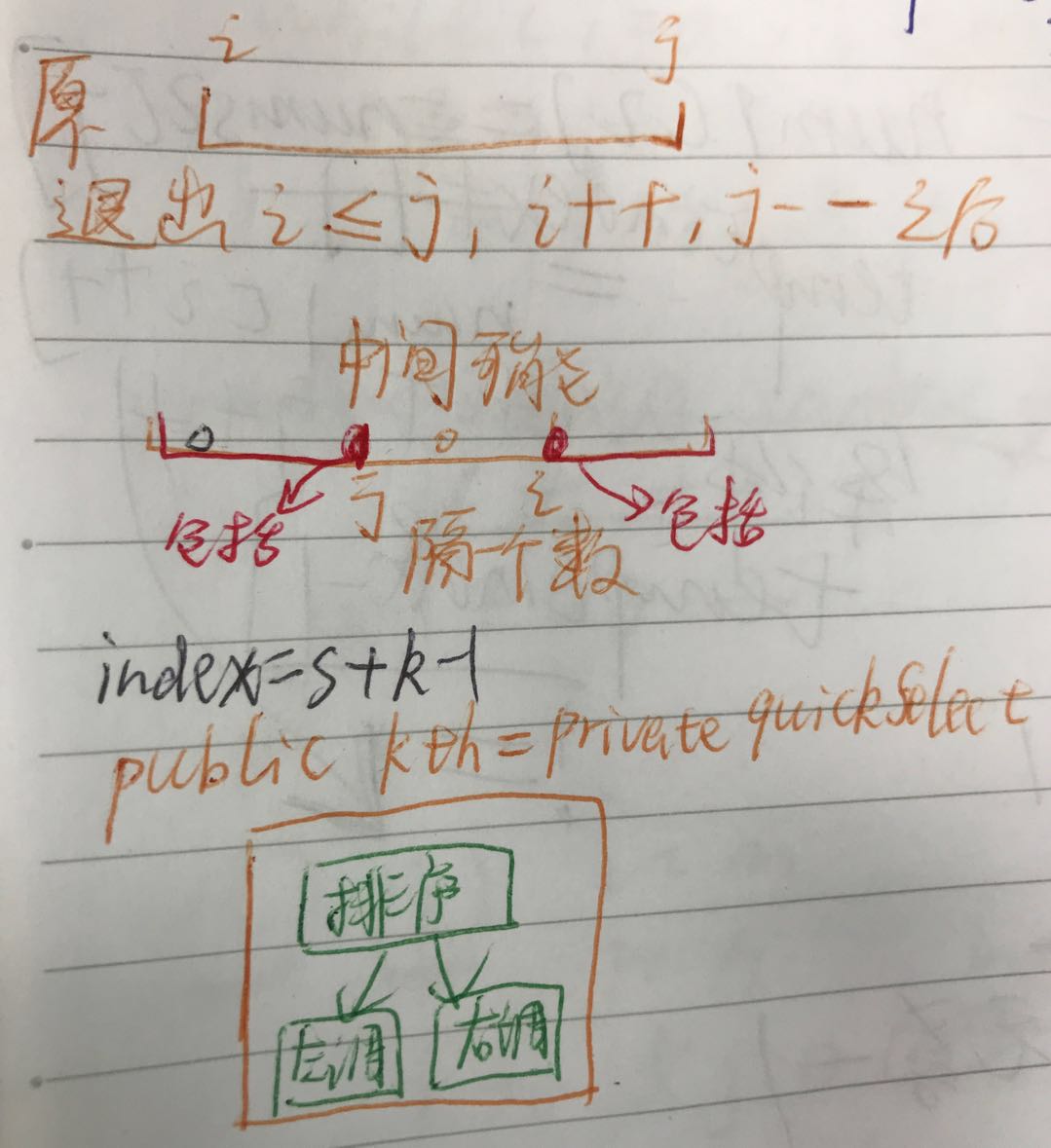

class Solution { public int findKthLargest(int[] nums, int k) { return quickSelect(nums, 0, nums.length - 1, k);} private int quickSelect(int[] nums, int start, int end, int k) { int i = start; int j = end; int pivot = nums[(start + end) / 2]; if (start == end) { return nums[start]; } //从小到大排序 while (i <= j) { while (i <= j && nums[i] > pivot) { i++; } while (i <= j && nums[j] < pivot) { j--; } if (i <= j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; i++; j--; } } if (start + k - 1 <= j) { return quickSelect(nums, start, j, k); } else if (start + k - 1 >= i) { return quickSelect(nums, i, end, k - (i - start)); } else return nums[j + 1]; } }




