关于PDH稳频原理

大概写于两年前。是对文献[1]的笔记。

PDH稳频技术

Fabry-Perot 腔的透射和反射特性

F-P干涉仪一般用于分光。两个波长分别为\(\lambda_1\)和\(\lambda_2\)的光入射至干涉仪，形成两套同心圆环组。假设\(\lambda_2>\lambda_1\)则同级干涉圆环而言，\(\lambda_2\)的直径更小。当\(\lambda_2\)波长增大，其第\(m\)级圆环将和\(\lambda_1\)的\(m+1\)级圆环重叠，从而无法分光。于是存在一最大分光波长差，即自由光谱范围FSR。

近正入射(\(\theta\approx0\))时的F-P腔的自由光谱范围用波长表示为\(\Delta \lambda_f=\lambda^2/(2nL)\)其中\(L\)为腔长度，可以取\(n=1\)，则换用频率则表示为\(\Delta\nu_\text{fsr}=c/2L\)。对于正入射的平面光波\({\bf E}_\text{int}(t)={ E}_\text{inc}\exp i({\bf k}\cdot{\bf r}-\omega t){\bf e}_1\)，设从腔整体接收到的反射光波为\({\bf E}_\text{ref}(t)={ E}_\text{ref}\exp i(-{\bf k}\cdot{\bf r}-\omega t){\bf e}_1\)，其中常相位因子被吸收进复振幅中。由平行平板多光束干涉的艾里(Airy)公式，反射前后复振幅有关系：

\[F(\omega)=\frac{E_\text{ref}}{E_\text{inc}}=\frac{r\left[\exp\left(i\frac{\omega}{\Delta\nu_\text{fsr}}\right)-1\right]}{1-r^2\exp\left(i\frac{\omega}{\Delta\nu_\text{fsr}}\right)} \]

其中\(r\)是腔镜的振幅反射系数（无吸收的对称腔\(r_1=r_2=r<0\)且\(r^2=R\)），\(F(\omega)\)称为腔的振幅反射系数，是复的。其模平方为光强的反射率，在无吸收镜面的条件下，反射光强分布和透射光强分布是互补的，即二者之和为入射光强分布。

物理上，反射光束分为两部分，一部分是迅速反射光束（入射光打到第一块镜就被反射回来），另一部分是腔泄漏光束（由于腔镜反射不完全而泄露出去的光）。这二者同频、同偏振、相位差恒定，发生干涉，干涉结果取决于相位差，相位差取决于入射光频率\(\omega\)。\(\omega\)变动，则相位差变动，时而干涉相长时而干涉相消。

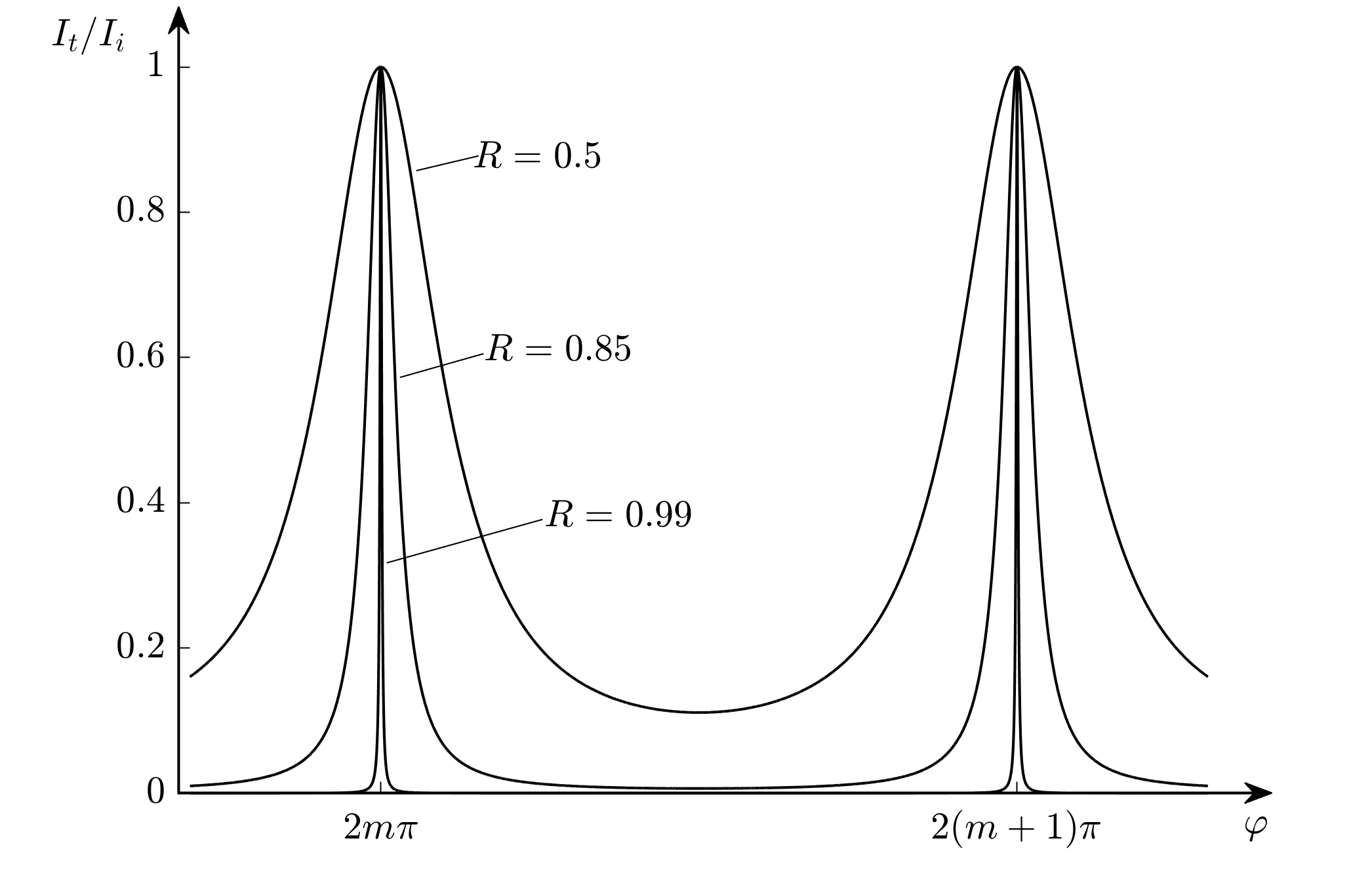
艾里公式中的相位\(\omega/\Delta\nu_\text{fsr}\)来自于\(\varphi=4\pi n h\cos\theta/\lambda\)，作出F-P腔的光强透过率和该\(\varphi\)的曲线，在\(R\sim1\)时取明条纹的半高全宽得到\(\epsilon=2(1-R)/\sqrt{R}\)，并引入精细度Finesse的定义：相邻二条纹的相位差(\(2\pi\))和条纹半高全宽之比，即\(N=\pi\sqrt{R}/(1-R)\). 镜面反射率\(R\)越大，条纹半高全宽越窄，精细度越高。在反射率很高、精细度很高的情况下，近似有\(N=\pi/(1-R)\)。

可以证明，当\(\omega\)变动时，\(F(\omega)\)取遍复平面上的一个圆，如下图。

该圆和虚轴相切，位于左半平面，圆心在实轴上。

在一般情形下(F-P腔非对称、有吸收)，腔整体的振幅反射系数为

\[F(\omega)=\frac{-r_{1}+r_{2}\left(r_{1}^{2}+t_{1}^{2}\right) \exp \left(i \frac{\omega}{\Delta \nu_{\mathrm{fsr}}}\right)}{1-r_{1} r_{2} \exp \left(i \frac{\omega}{\Delta \nu_{\mathrm{fsr}}}\right)} \]

发现满足\(|F-Z_0|^2=R_0^2\)，其中\(Z_0\)和\(R_0\)都是实数，

\[\begin{aligned}&Z_{0}=-\frac{r_1}{1-r_{1}^{2} r_{2}^{2}}\left[1-r_{2}^{2}\left(r_{1}^{2}+t_{1}^{2}\right)\right] \\ &R_0=\frac{t_{1}^{2} r_{2}}{1-r_{1}^{2} r_{2}^{2}}\end{aligned} \]

在无吸收、对称腔条件下\(|Z_0|=|R_0|\)，即圆切于虚轴。注意无吸收的对称腔当\(\omega\sim2\pi N\Delta\nu_\text{fsr}\)时，\(F(\omega)\)在原点附近，若把\(\omega\)写为\(\omega=2\pi N\Delta\nu_\text{fsr}+\delta\omega\)，带入\(F(\omega)\)中把指数展开则得到\(F(\omega)\approx\text{i}{\delta\omega}/[{\Delta\nu_\text{fsr}(1-r^2)}]\)是纯虚的。

背景

现代激光器是可调的，都有端口可以馈入频率和强度的变换以校正并稳定。当入射光频率与腔共振时，即\(\nu=\omega/2\pi=N\Delta\nu_\text{fsr}\)，则反射光束强度为零[\(F(\omega)=0\)]，透射光束强度达到最大。稍稍偏离共振频率，则透射光束强度减小地很快，其中有一段大斜率的近似线性区。由此可以把激光频率通过一个参考腔锁定在共振频率上，这是PDH之前的做法。但是这种做法有缺陷，考虑到激光器的输出功率也在波动，该方法无法区分透射光强的变化究竟是频率偏移造成的还是输出功率波动造成的。

因此改进的办法可以使用反射光束，如下图所示。反射光束在严格共振时强度为零，在稍稍偏移共振的近共振区强度迅速增大。反馈系统的目标只要把反射光束强度锁定为零即可。但是这里还有一个问题，就是如何区分激光的对共振频率的偏移，是正的还是负的。观察图像，反射光束强度本身关于共振位置是对称的，但是其导数是反对称的，可以加以利用。利用其导数的方法是间接的：给入射光加以很小的频率调制（正弦的），则反射光束强度也被调制（在近似线性区也是正弦的），如果偏移\(\delta=\omega-\omega_0\)是正的，则这两个信号同相，如果偏移\(\delta\)是负的，则反相。这为PDH技术提供了思路。

PDH稳频的过程

前面说的是调频，在实际中由于简便起见，常常是调相，二者没有本质区别。使用图中的电光调制（Pockels盒）给入射光加以含时间的相移

\[E_\text{inc}(t)=E_0\exp \mathrm{i}(\omega t+\beta\sin\Omega t) \]

其中\(\beta\)是电光调制的深度（是一个小量），\(\Omega\)是电光调制中本振的频率。使用Bessel函数可以展开为

\[E_\text{inc}(t)\approx[J_0(\beta)+2iJ_1(\beta)\sin\Omega t]E_0e^{i\omega t}\\=E_0[J_0(\beta)e^{i\omega t}+J_1(\beta)e^{i(\omega+\Omega)t}-J_1(\beta)e^{i(\omega-\Omega)t}] \]

近似的好坏取决于调制深度\(\beta\)有多小，可以发现，当\(\beta\)足够小时，入射光分为三个频率分量：\(\omega\)的载波，两个\(\omega\pm\Omega\)的边带。注意载波能量比边带能量大得多，因为\(J_0(0^+)=1,J_1(0^+)=0\)。

三个频率分量对应的光强分别为：

\[P_c=J_0^2(\beta)P_0\\ P_s=J_1^2(\beta)P_0 \]

其中\(P_0=|E_0|^2\)是调制前的入射光强，\(P_c\)为\(\omega\)频率分量对应的光强，\(P_s\)为\(\omega\pm\Omega\)频率分量对应的光强。

F-P腔作为一个线性时不变（LTI）系统，我们已经知道了它的频率响应，因此对入射其中的三个频率分量的响应就是：

\[E_\text{ref}(t)=E_0\left[F(\omega)J_0(\beta)\exp(i\omega t)+F(\omega+\Omega)J_1(\beta)\exp i(\omega+\Omega )t-F(\omega-\Omega)J_1(\beta)\exp i(\omega-\Omega)t\right] \]

实际上光电探测器测得的是反射光的功率，因此把上式求模平方，得到光电管输出的电信号为

\[P_\text{ref}(t)=P_c[F(\omega)]^2+P_s\{|F(\omega+\Omega)|^2+|F(\omega-\Omega)|^2\}\\+2\sqrt{P_cP_s}\{\text{Re}[G(\omega,\Omega)]\cos\Omega t+\text{Im}[G(\omega,\Omega)]\sin\Omega t\}\\+P_s\cdot(2\Omega~\text{terms}) \]

其中\(G(\omega,\Omega)=F(\omega)F^*(\omega+\Omega)-F^*(\omega)F(\omega-\Omega)\). 按照顺序，上式前两个\(P_c,P_s\)项不含时间，是直流项，可以通过低通滤波器滤除；最后的振幅为\(P_s\)的项频率为\(2\Omega\)，但是振幅相比较中间的\(\sqrt{P_cP_s}\)而言很小，可以忽略。中间的振幅为\(\sqrt{P_cP_s}\)的项是重点，其振荡频率为\(\Omega\)，既包含正弦振荡的也包含余弦振荡的，其振幅是\(G(\omega,\Omega)\)的实部或者虚部，它称为误差信号。称之为“信号”是相对于激光器频率\(\omega\)而言的，即给定电光调制的信号源频率\(\Omega\)后，对于每个激光器频率\(\omega\)，误差信号\(G(\omega,\Omega)\)都给出不同的值，反映出对当前频率\(\omega\)的“鉴定”信息。

于是先描述如何通过\(G(\omega,\Omega)\)的实部或虚部来实现稳频（即误差信号的形状如何），再描述\(G(\omega,\Omega)\)的实部或虚部如何作为电压信号提取出来。

（1）当调制频率\(\Omega\)很小时有

\[G(\omega,\Omega)\approx 2 \Omega\operatorname{Re}\left\{F(\omega) \frac{\mathrm{d}}{\mathrm{d} \omega} F^{*}(\omega)\right\} \approx \Omega \frac{\mathrm{d}|F(\omega)|^{2}}{\mathrm{d} \omega} \]

是实数，因此\(P_\text{ref}\)中的\(\sin\Omega t\)振荡项为零，而\(\Omega\)频率分量仅剩余\(\cos\Omega t\)项，从而误差信号为\(2\sqrt{P_cP_s}\Omega\cdot\text{d}|F|^2/\text{d}\omega\)，而\(\text{d}|F|^2/\text{d}\omega\)随载波频率\(\omega\)的变化如下图（R=0.994，注意图中横坐标尺度为1e-3）

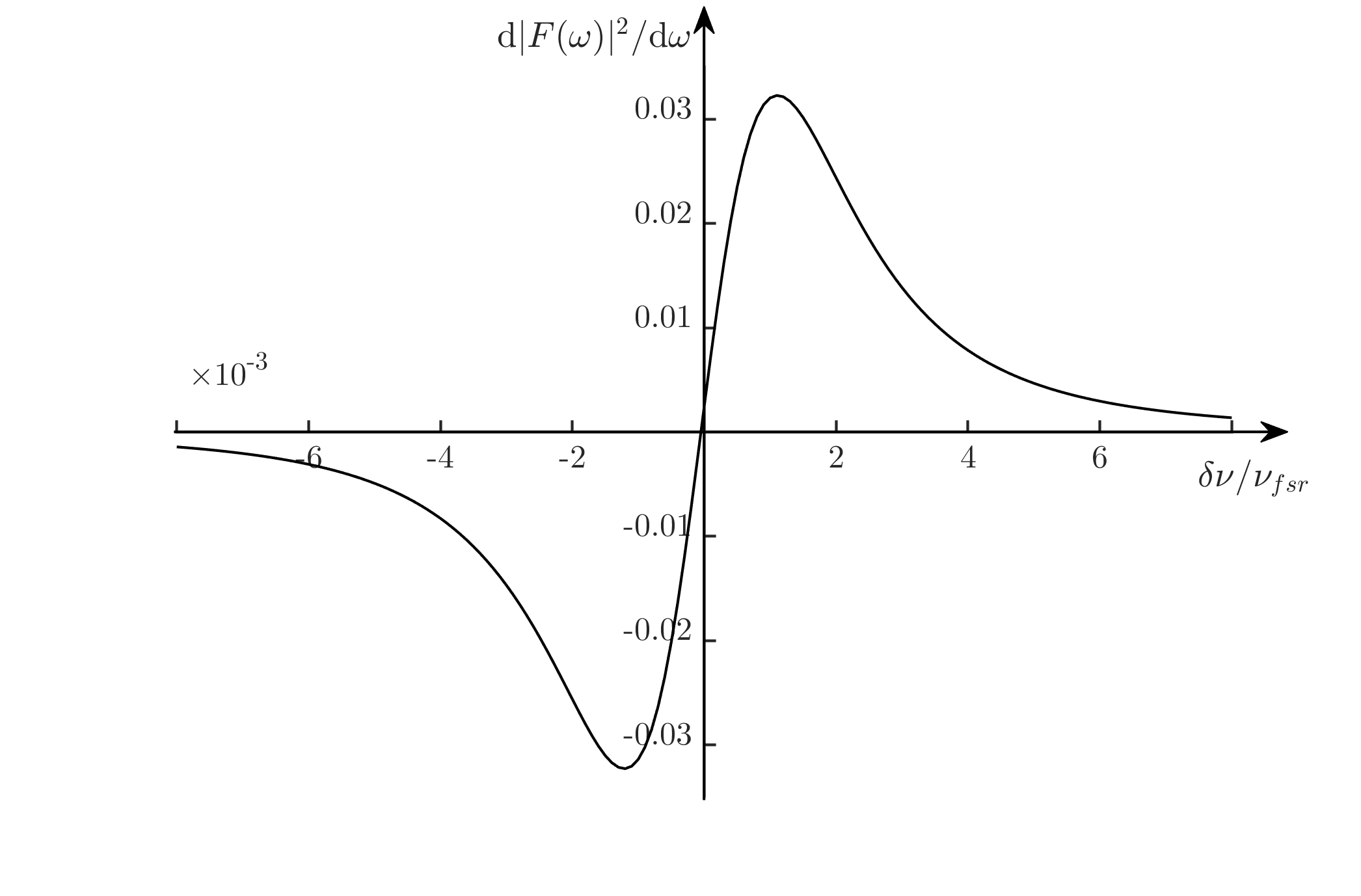
可见当\(2\pi\nu=\omega\)偏离腔的共振频率时，误差信号迅速增大。这时引入PID锁定环路，将该误差信号锁到0的位置，就实现了稳频。锁定到横坐标上的\(\pm10^{-4}\)以内，则厘米级的F-P腔就能提供MHz量级的频率稳定性。

（2）当调制频率\(\Omega\)很大，以至于边带错过了透射窗口，被全部反射回去，则有\(F(\omega\pm\Omega)\approx-1\), 于是

\[G(\omega,\Omega) \approx-2\text{i}\text{Im}[F(\omega)] \]

是纯虚的，这时只剩\(\sin\Omega t\)振荡。下图给出\(G(\omega,\Omega)\)曲线，图中参数\(R=0.994\), \(\Omega=0.04\Delta\nu_\text{fsr}\)，这时鉴频斜率远大于前一种低频调制情形。

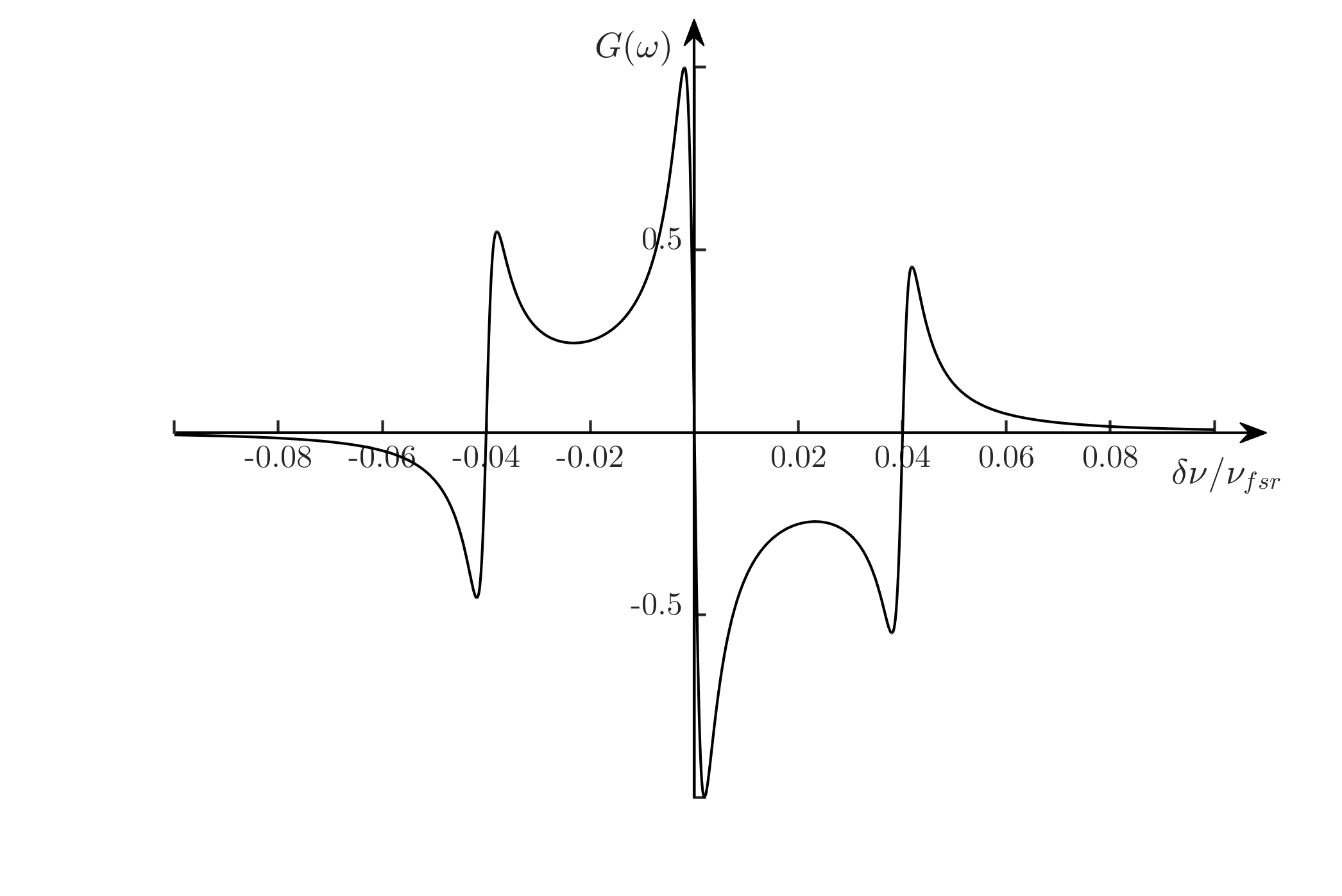
最后就是误差信号如何提取。首先它是频率为\(\Omega\)的信号分量的幅值，于是只需将其和一相位正交的同频信号混频（一般就使用前面电光调制器的信号源，经过90°移相），再经过一低通滤波，得到的直流信号功率就正比于\(G(\omega,\Omega)\)。如果要观察误差信号的形状，则可以令激光器在腔共振频率附近扫频（即扫\(\omega\)），将误差信号接入示波器即可。

Ref:

[1]. An introduction to PDH laser frequency stabilization (2000).