Dressed Atom和远失谐光位移

Dressed atom 和远失谐光位移

半经典处理

全哈密顿为

\[H=\frac{1}{2}\hbar\omega_0\sigma_z-\vec{p}\cdot\vec{E} \]

其中\(\vec{E}=\vec{E_0}\cos(\omega t)\)，已经取了偶极近似。在旋波近似下简化为

\[H=\frac{1}{2}\hbar\omega_0\sigma_z+\frac{1}{2}\hbar(\Omega\sigma_-\text{e}^{i\omega t}+\Omega^*\sigma_+\text{e}^{-i\omega t}) \]

其中Rabi频率\(\Omega=e/\hbar\langle g|\vec{r}|e\rangle\cdot\vec{E}_0\)，它可以取为实数。

为求解这样的薛定谔方程，先对哈密顿进行分割

\[H=\frac{1}{2}\hbar\omega\sigma_z-\frac{1}{2}\hbar\delta\sigma_z+\frac{1}{2}\hbar(\Omega\sigma_-\text{e}^{i\omega t}+\Omega^*\sigma_+\text{e}^{-i\omega t}) \]

以上式第一项作为自由哈密顿部分，变换到相互作用绘景中去，得到相互作用绘景中哈密顿为

\[H_I=-\frac{1}{2}\hbar\delta\sigma_z+\frac{1}{2}\hbar\Omega(\sigma_-+\sigma_+) \]

上面哈密顿不含时间，直接在相互作用绘景中求解问题，再变换回薛定谔绘景得到原问题的解为

\[|\psi(t)\rangle=\begin{aligned} &\left(a \cos \theta e^{-i E_{1}^{+} t / \hbar}-b \sin \theta e^{-i E_{1}^{-} t / \hbar}\right)|g\rangle \\ &+\left(a \sin \theta e^{-i E_{2}^{+} t / \hbar}+b \cos \theta e^{-i E_{2}^{-} t / \hbar}\right)|e\rangle \end{aligned} \]

其中系数\(a,b\)为任意系数，满足归一化条件；参数\(\theta\)满足\(0\leqslant \theta\leqslant\pi/2\)，且有

\[\cos\theta=\sqrt{\frac{\Omega'+\delta}{2\Omega'}},\quad\sin\theta=\sqrt{\frac{\Omega'-\delta}{2\Omega'}} \]

其中\(\Omega'=\sqrt{\Omega^2+\delta^2}\)为有效Rabi频率。四个能量参数如下：

\[\left\{\begin{aligned} E_1^+=\frac{\hbar}{2}(-\omega_0+\Omega'-\delta)=\frac{\hbar}{2}(-\omega+\Omega')\\ E_1^-=\frac{\hbar}{2}(-\omega_0-\Omega'-\delta)=\frac{\hbar}{2}(-\omega-\Omega')\\ E_2^+=\frac{\hbar}{2}(\omega_0+\Omega'+\delta)=\frac{\hbar}{2}(\omega+\Omega')\\ E_2^-=\frac{\hbar}{2}(\omega_0-\Omega'+\delta)=\frac{\hbar}{2}(\omega+\Omega')\\ \end{aligned}\right. \]

注意这里的含时解并不具备一般不含时问题下解的一般形式，即不能写成几个不含时态乘以各自的含时相位因子再取线性组合的形式。

量子处理

电磁场量子化以后，电场为\(\vec{E}(t)=i\sqrt{\frac{\hbar\omega}{2\epsilon_0V}}\tilde{\vec{E}}_0(a-a^\dagger)\), 其中\(\tilde{\vec{E}}_0\)是单位电场矢量，同样取旋波近似，全哈密顿为

\[H=\frac{1}{2}\hbar\omega_0\sigma_z+\hbar\omega aa^\dagger+i\hbar\lambda(\sigma_+a_--\sigma_-a^\dagger) \]

也即 Jaynes-Cummings 模型，哈密顿不含时间。其中的耦合常数\(\lambda=e\langle g|\vec{r}|e\rangle\cdot\tilde{\vec{E}}_0\sqrt{\frac{\omega}{2\hbar\epsilon_0V}}\)。

选取基矢量为原子态和光场光子数态的直积态，发现上面哈密顿只将诸如态\(|g\rangle|n+1\rangle\)和态\(|e\rangle|n\rangle\)耦合，或者说，在这样排序的基矢组下，哈密顿总是\(2\times2\)分块对角的，仅需将每个块对角化即可。在态\(|g\rangle|n+1\rangle\)和态\(|e\rangle|n\rangle\)下，哈密顿写为

\[H=\hbar\begin{pmatrix} n\omega+\frac{1}{2}\omega_0&i\lambda\sqrt{n+1}\\ -i\lambda\sqrt{n+1}&(n+1)\omega-\frac{1}{2}\omega_0 \end{pmatrix} \]

其本征值为

\[E^\pm_n=(n+\frac{1}{2})\hbar\omega\pm\frac{\hbar}{2}\Omega_n'(\delta) \]

因为其和\(n\)有关，所以加了下标. 其中\(\Omega'_n(\delta)=\sqrt{\delta^2+(2\lambda)^2(n+1)}\)，相当于半经典处理的有效Rabi频率，为了验证这一点，做如下考虑。

经典电场为\(\vec{E}(t)=\vec{E}_0\sin\omega t=\tilde{\vec{E}}_0E_0\frac{i}{2}(\text{e}^{-i\omega t}-\text{e}^{i\omega t})\), 相互作用绘景中量子化后电场为\(\vec{E}(t)=i\sqrt{\frac{\hbar \omega}{2\epsilon_0V}}\tilde{\vec{E}}_0(a\text{e}^{-i\omega t}-a^\dagger\text{e}^{i\omega t})\)，两者对比得到

\[\vec{E}_0\equiv\tilde{\vec{E}}_0E_0\sim2a^\dagger\sqrt{\frac{\hbar\omega}{2\epsilon_0V}}\tilde{\vec{E}}_0\sim2\sqrt{n+1}\sqrt{\frac{\hbar\omega}{2\epsilon_0V}}\tilde{\vec{E}}_0 \]

利用上面关系代入可得

\[\Omega'_n(\delta)=\sqrt{\delta^2+\left(2\sqrt{n+1}\sqrt{\frac{\omega}{2\hbar\epsilon_0V}}e\langle g|\vec{r}|e\rangle\cdot\tilde{\vec{E}}_0\right)^2}\sim\sqrt{\delta^2+\Omega^2}=\Omega' \]

因此这里的\(\Omega'_n(\delta)\)就相当于半经典处理的\(\Omega'\)，以后都记为\(\Omega'\).

此外可由本征态解得

\[|\psi(t)\rangle=\begin{aligned} &\left(a \cos \theta e^{-i E^{+}_n t / \hbar}-b \sin \theta e^{-i E^{-}_n t / \hbar}\right)|e\rangle|n\rangle \\ &+\left(a \sin \theta e^{-i E^{+}_n t / \hbar}+b \cos \theta e^{-i E^{-}_n t / \hbar}\right)|g\rangle|n+1\rangle \end{aligned} \]

参数\(a,b,\theta\)和半经典处理那里是一样的，解的结构也是类似的，除了这里的能量因子是\(E_n^\pm\)。但是半经典处理中是不考虑光场本身能量，因此半经典处理中的\(E^\pm_{1，2}\)中可以加减整数倍的\(\hbar\omega\)，于是就和量子处理得到的能量一致了。

另外量子处理有一点，就是解可以写为不含时态乘以含时相位因子的线性组合，因为这里的哈密顿是不含时间的，所以在量子处理中，可以看到原先的两个能级\(|e\rangle|n\rangle\)和\(|g\rangle|n+1\rangle\)（能级间隔是\(\hbar\delta\)），现在因为相互作用的出现，发生了重组，新能级之间的间隔为\(\hbar\Omega'\)。

如果固定失谐（按\(\delta\)正负分情况），画出\(E_{1,2}^\pm\)随\(\Omega'\)变化的关系如下图。注意按照量子处理来看，实际上能级图在纵轴上是以\(\hbar\omega\)为周期的。

图略。

如果固定\(\Omega'\)（表征耦合强度），则能级随\(\delta\)的变化关系如下。

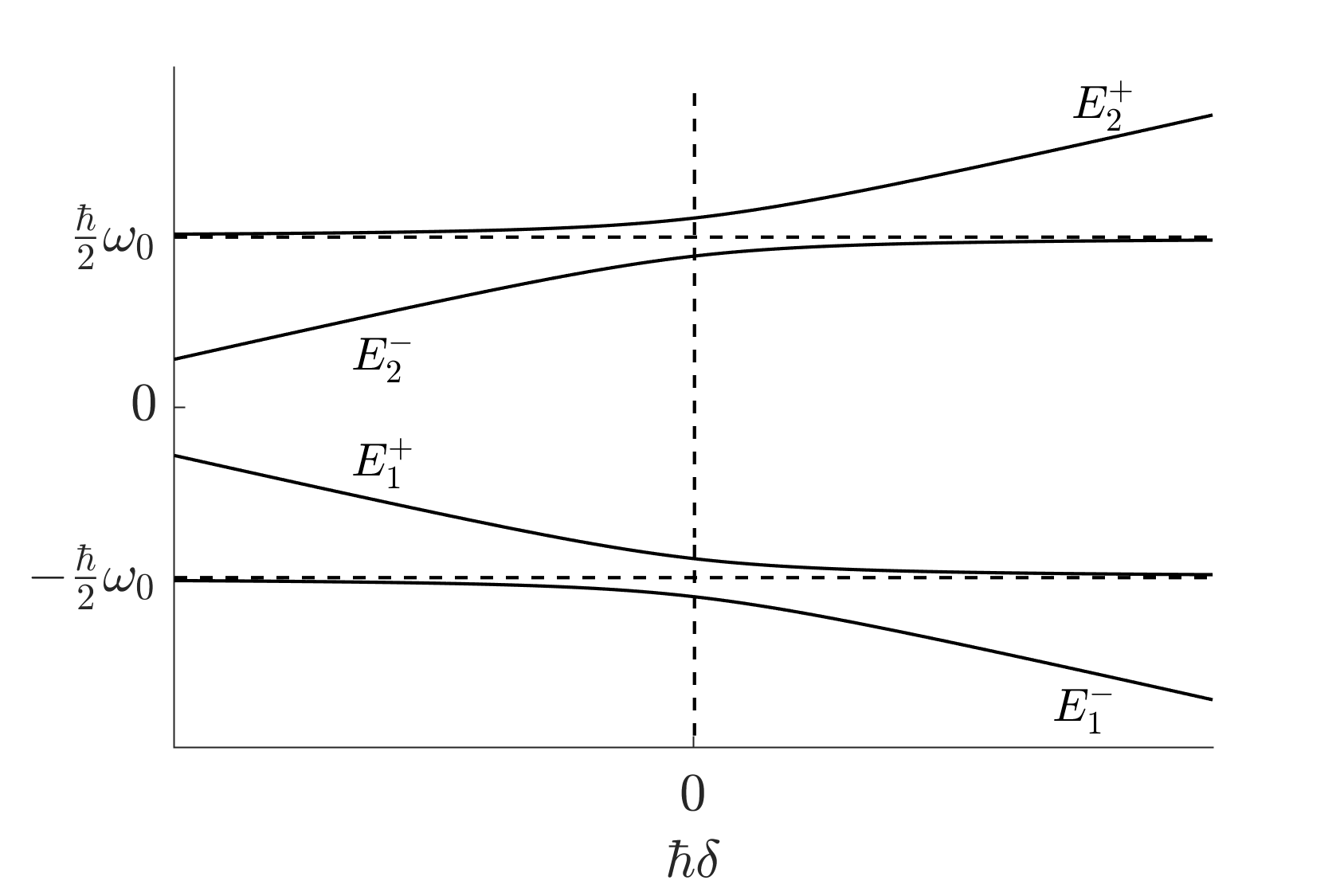
现在关注失谐远大于Rabi频率的极限情况，即极限\(|\delta|\gg\Omega\)。这时若正失谐\(\delta>0\)，\(\cos\theta=1\)，\(\sin\theta=0\)，即原来解中的四项有两项趋于零，导致能量因子只剩\(E_1^+\)和\(E^-_2\)两个，各自相对于原来的能级\(\mp\frac{1}{2}\hbar\omega_0\)有大小为\(\frac{\hbar\Omega^2}{4\delta}\)的微小移动，相互靠近。若负失谐\(\delta<0\)，则剩余两能级为\(E_1^-\)和\(E_2^+\)，它们互相远离，各自移动了\(\frac{\hbar\Omega^2}{4|\delta|}\), 这恰好和远失谐情况下计算得到的光位移相等。然而需要注意的是，这里的远失谐必须保证旋波近似RWA依然成立，因为上面这些的导出是建立在RWA的基础上。RWA的核心是假设\(\frac{1}{|\omega-\omega_0|}\gg\frac{1}{\omega+\omega_0}\)，这要求\(\omega\approx\omega_0\)，当失谐极远以至于\(\frac{1}{|\omega-\omega_0|}\)和\(\frac{1}{\omega+\omega_0}\)基本同一量级，则RWA不在成立，上面的推导也就失去了基础。这时的光频移常常通过“极化率理论”来计算，在那里将不再使用RWA，详见另一篇笔记。