塞曼效应以及能级的计算
简单总结了一下在原子结构的基础上的Zeeman效应。很久之前就知道,这次算是复习,顺便计算一下。仅限于LS耦合,并且假设核自旋是0. 后面可能会考虑上核自旋非零的原子。
弱场下原子的Zeeman效应
把电子运动视为经典带电小球的圆周运动,按照电磁学,得到的磁矩为\(\boldsymbol{\mu}=q/(2m_e)\boldsymbol{\ell}\),其中\(q=-e\)为电子电荷,\(m_e\)为电子质量。该磁矩还可以改写为\(\boldsymbol{\mu}=q\hbar/(2m_e)\boldsymbol{\ell}/\hbar=-\mu_B\boldsymbol{\ell}/\hbar\) ,其中\(\mu_B\)为玻尔磁子,取正值。于是相互作用能量(选取外磁场沿\(z\)轴)为\(H'=-\boldsymbol{B}\cdot\boldsymbol{\mu}=eB_z/(2m_e)\ell_z\)。这是从经典图像中得到的结果。按照B.卡尼亚克《原子物理学(下册)》,直接分析静磁场中单电子的Schrodinger方程,可以得到两个附加项,一项为\(H'=-\boldsymbol{B}\cdot\boldsymbol{\mu}=eB_z/(2m_e)\ell_z\),另一项正比于磁场平方。这两项分别为顺磁项和抗磁项。简单的计算表明,对于\(1T\)的磁场而言,第二项远小于第一项,因此略去。不论从哪里出发,得到的附加哈密顿是相同的。在多电子情形下即为
进一步考虑各个电子的自旋,最终得到
其中\(g_\text{s}\)为电子自旋的Lande因子,值为2. 在Slater的Quantum Theory of Atomic Structure中,从磁场中单电子的Dirac方程出发,计算电流密度,分别得到电子轨道角动量贡献的磁矩(和这里一样)以及自旋贡献的磁矩,其中自旋磁矩含有值为2的Lande因子。也可以说电子轨道磁矩的Lande因子为1. 至此已经给出了磁场中哈密顿的附加项的来源,并说清了电子Lande因子的来源。
现在看LS耦合情形下,弱场Zeeman效应。弱场意味着磁场的附加哈密顿是所有微扰中最小的,因此最后考虑。如此考虑的必要条件是,磁场带来的精细结构态内部的能级分裂远小于不同精细结构态之间的能级间隔。LS耦合下一个精细结构子空间由\(J^2\)和\(J_z\)的共同本征态张成,它们有共同的\(J\)量子数,不同的\(m_{J}\)量子数,是简并的。限定在一个精细结构子空间内讨论,这样,基矢为\(\{|E^0_J,J,m_J\rangle\}\),其中\(E^0_J\)是该精细结构能级的简并能量,其实这个位置本来应该是包括\(L,S\)值在内的其他量子数。
由于Wigner-Eckart定理,两个同秩的不可约张量算符的各个分量在角动量基矢\(|\alpha,J,m_J\rangle\)上的矩阵元的比值相等,即(假设\(k\)秩)
其中常数\(C\)和\(q,m_J,m'_J\)无关。下面选取\(U^{(k)}_q\)为一秩的总角动量算符\(J_q\), 则有
其中\(\hat{\boldsymbol{A}}\)是某矢量算符。因为其他量子数或者\(J\)量子数的正交性,上式中\(\alpha',J'\)的撇号可以略去而不损失一般性。计算
所以
因为现在只在某精细结构子空间中讨论问题,因此上式可以直接写为
称为Lande公式或者投影定理,它有重要的物理意义:矢量\(\boldsymbol{A}\)有意义的部分仅仅是其在角动量上的投影。
由上面Wigner-Eckart定理的分析,可知在某精细结构子空间中,外加磁场的附加哈密顿\(H'=({\mu_B}/{\hbar}){B}_z\sum_i ({\ell}_{iz}+g_\text{s}{s}_{iz})=({\mu_B}/{\hbar}){B}_z(L_z+g_sS_z)\)的矩阵元的计算可写为
其中\(g_J\)就是算符\((L_z+g_sS_z)\)和算符\(J_z\)之间所相差的因子\(C\),也称为Lande因子,它其实也是总磁矩和总角动量之比的度量。上式中有\(\delta\)符号,因此在一个精细结构子空间中,如果选取\(J^2,J_z\)共同本征态则附加哈密顿自动对角化,每个\(m_J\)量子数有自己的能量修正,简并解除。
剩下的是Lande因子$g_J \(的计算。因为Lande因子就是\)C$,所以
先看分子,\((\hat{\boldsymbol{L}}+g_s\hat{\vec{S}})\cdot\hat{\vec{J}}=\hat{\vec{J}}\cdot[\hat{\vec{J}}+(g_s-1)\hat{\vec{S}}]\),另一方面取\(\hat{\vec{L}}=\hat{\vec{J}}-\hat{\vec{S}}\)两边平方有\(\hat{\vec{J}}\cdot\hat{\vec{S}}=(\hat{\vec{J}}^2+\hat{\vec{S}}^2-\hat{\vec{L}}^2)/2\),因此
而在精细结构子空间中,这些角动量的平方都是守恒量,因此直接有
至此计算完成,LS耦合下引入外磁场,对称性缩小,每个原本简并的精细结构子空间发生分裂,不同的\(m_J\)量子数有不同的能量修正。
强场下的Zeeman效应
考虑强外磁场,这时认为附加哈密顿小于剩余静电势,但大于LS耦合的附加哈密顿。因此在谱项空间内先考虑外磁场的附加哈密顿,再考虑LS耦合的附加哈密顿。谱项空间的简并度为\((2S+1)(2L+1)\),选取基矢为非耦合基矢\(|E_0LSm_Lm_S\rangle\),好处是\(\hat{L}_z\)和\(\hat{S}_z\)算符自动对角化,而外磁场附加哈密顿恰好是\(({\mu_B}/{\hbar}){B}_z(L_z+g_sS_z)\)。
既然自动对角化,则可以直接写出一级修正为\(\mu_BB_z(m_L+2m_S)\),需要注意的是可能会有几个能级的一级修正相同,即未能完全解除简并。
下一步再考虑LS耦合的附加哈密顿\(\sum_i\xi_i\vec{\ell}_i\cdot\vec{s}_i\),因为仅在谱项空间内考虑问题,利用Wigner-Eckart定理,可以改写该附加哈密顿为\(A'\vec{L}\cdot\vec{S}\),其中\(A’\)为某常数。因为前面外磁场的微扰已经使得能级部分解除简并了,对于非简并的态,能量修正可以直接计算如下
简并的态单独考虑。首先\(L_zS_z\)必然自动对角化,其次计算\(L_xS_x\)和\(L_yS_y\)的矩阵元。以\(L_xS_x\)为例
若其中的\(L_+S_+\)在某两个简并态之间的矩阵元非零,则必然有\(m_L=m_L'+1\), \(m_S=m_S'+1\)成立。另一方面,因为这两个态简并,所以必然有\(\mu_BB_z(m_L+2m_S)=\mu_BB_z(m_L'+2m_S')\),这二式矛盾。因此\(L_+S_+\)在任意两个简并的态之间的矩阵元为零,其他三项同理,于是对于简并的情况,能量修正依然是\(Am_Lm_S\)。
总结起来,强场下的谱项分裂能量间隔为\(\mu_BB_z(m_L+2m_S)+Am_Lm_S\)。
中间情况
如果LS耦合项与外磁场引入的附加哈密顿大小相当,则需要同时作为微扰处理,即在谱项空间中计算其矩阵元。计算矩阵元时通常选择耦合表象基矢来计算,在该组基矢下,\(A'\vec{L}\cdot\vec{S}\)是对角的,矩阵元为
但是\(({\mu_B}/{\hbar}){B}_z(L_z+g_sS_z)\)不是对角的,为了计算其在某两个基矢之间的矩阵元,通常使用CG系数将基矢展开为非耦合表象基矢的线性叠加,再进行计算。计算完成后将矩阵对角化,即可得到所有的能量修正。
需要注意的是即使施加了这两个微扰,系统仍有沿着外磁场方向的柱对称性,也就是说\(J_z\)和全哈密顿对易,是守恒量,而\(m_J\)是好量子数。因此微扰哈密顿在不同\(m_J\)态之间的矩阵元为零,所以若将基矢按\(m_J\)排列,则微扰哈密顿是按\(m_J\)分块对角的,此时仅需要将各块对角化即可。
附:中间耦合的MATLAB计算代码。仅供参考,如有错误请告知。
%--------------------------------------
% CG.m 计算CG系数
%--------------------------------------
function ret = CG(j1,j2,m1,m2,j,m)
if m1+m2~=m
ret=0;
else
c=0;
for z=max([0,j2-j-m1,j1+m2-j]):min([j1+j2-j,j1-m1,j2+m2])
c=c+(-1)^z/(gamma(z+1)*gamma(j1+j2-j-z+1)*gamma(j1-m1-z+1)*gamma(j2+m2-z+1)*gamma(j-j2+m1+z+1)*gamma(j-j1-m2+z+1));
end
ret=c*sqrt((2*j+1)*gamma(j1+j2-j+1)*gamma(j+j2-j1+1)*gamma(j+j1-j2+1)/gamma(j+j1+j2+1+1))*sqrt(gamma(j+m+1)*gamma(j-m+1)*gamma(j1+m1+1)*gamma(j1-m1+1)*gamma(j2+m2+1)*gamma(j2-m2+1));
end
end
%--------------------------------------------------------
% H_B.m 计算外磁场附加哈密顿的矩阵元
%--------------------------------------------------------
function ret = H_B(j1,j2,j,m,j_,m_)
% 只在谱项空间内计算,即LS给定。因此只有j1,j2,无j1',j1'.
% 返回值的单位为u*B,u为玻尔磁子(取正值),B为外磁场。如返回1.5,则矩阵元为1.5uB.
% 实际上m_j是好量子数,不同m_j的态之间矩阵元为零。因此实际上这里m和m_只需保留一个即可。
right_vec=zeros((2*j1+1),(2*j2+1));
num_i=1;
for m_r=-j1:j1
num_j=1;
for m_c=-j2:j2
right_vec(num_i,num_j)=CG(j1,j2,m_r,m_c,j_,m_)*(m_r+2*m_c);
num_j=num_j+1;
end
num_i=num_i+1;
end
left_vec=zeros((2*j1+1),(2*j2+1));
num_i=1;
for m_r=-j1:j1
num_j=1;
for m_c=-j2:j2
left_vec(num_i,num_j)=CG(j1,j2,m_r,m_c,j,m);
num_j=num_j+1;
end
num_i=num_i+1;
end
ret=sum(sum(left_vec.*right_vec));
end
%--------------------------------------------------------
% Zeeman.m 计算能量本征值
%--------------------------------------------------------
function energy = Zeeman(L,S,B)
% B单位为T,Boh磁子为u
A=200e-25; %这里随便设一个数字
u=9.27400949e-24;% Bohr
J_max=L+S;
J_min=abs(L-S);
J_tab=J_min:J_max;
block_diag=cell(1,round(2*J_max+1));
num=0;
for m_j=-J_max:J_max
num=num+1;
if abs(m_j)>=J_min
block_diag{num}=zeros(round(J_max-abs(m_j)+1));
for J=abs(m_j):J_max
block_diag{num}(J-abs(m_j)+1,J-abs(m_j)+1)=0.5*A*(J*(J+1)-L*(L+1)-S*(S+1));
end
for J1=abs(m_j):J_max
for J2=abs(m_j):J_max
block_diag{num}(J1-abs(m_j)+1,J2-abs(m_j)+1)=block_diag{num}(J1-abs(m_j)+1,J2-abs(m_j)+1)+B*u*H_B(L,S,J1,m_j,J2,m_j);
end
end
else
block_diag{num}=zeros(length(J_tab));
for J=J_tab
block_diag{num}(J-min(J_tab)+1,J-min(J_tab)+1)=0.5*A*(J*(J+1)-L*(L+1)-S*(S+1));
end
for J1=J_tab
for J2=J_tab
block_diag{num}(J1-min(J_tab)+1,J2-min(J_tab)+1)=block_diag{num}(J1-min(J_tab)+1,J2-min(J_tab)+1)+B*u*H_B(L,S,J1,m_j,J2,m_j);
end
end
end
end
energy=[];
for i=1:length(block_diag)
[~,val]=eig(block_diag{i});
energy=[energy,(diag(val))'];
end
end
%--------------------------------------------------------
% run.m 运行代码
%--------------------------------------------------------
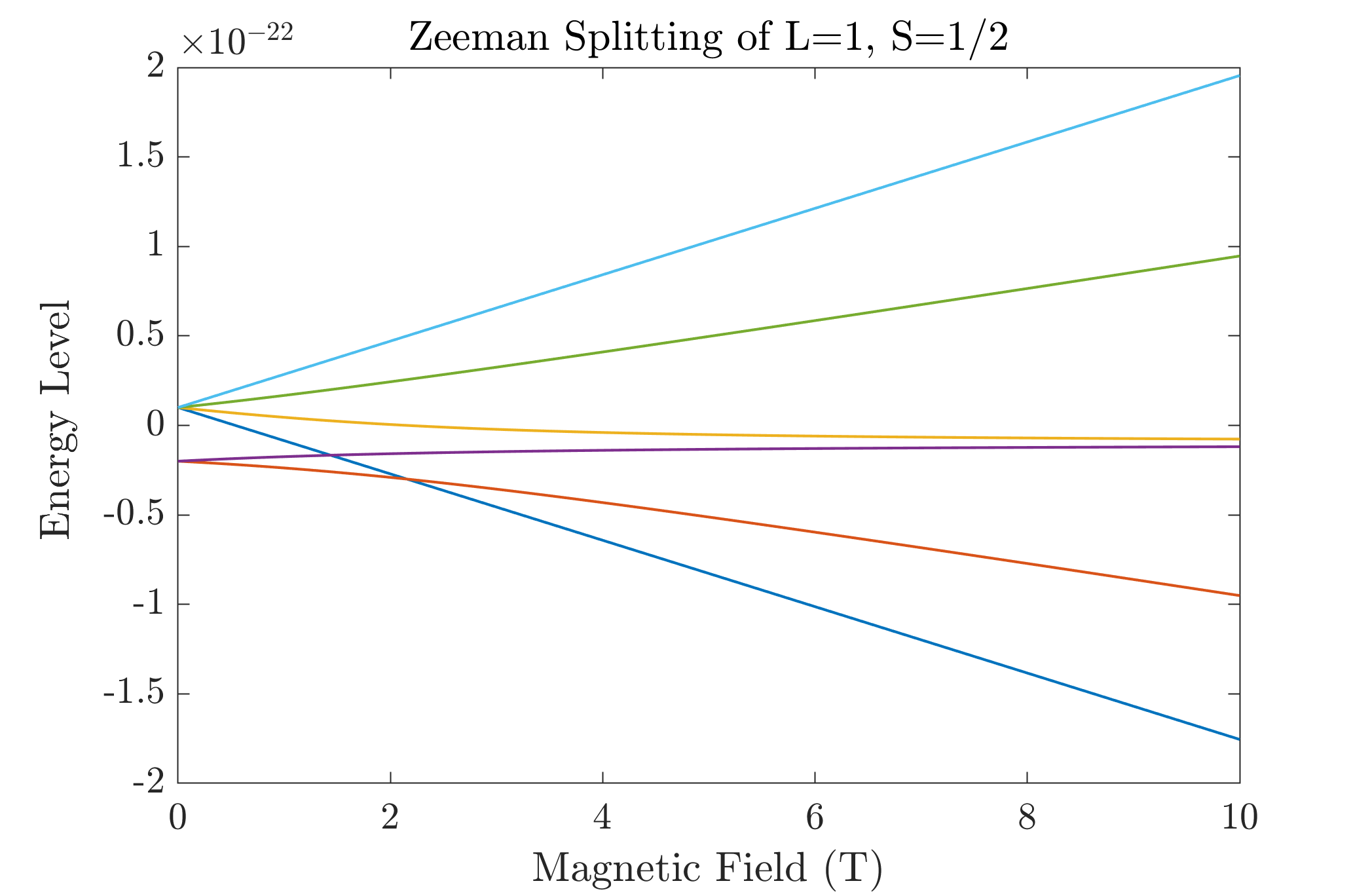
clear all;
B=[0:500:100000]*1e-4;
L=1;
S=1/2;
for i=1:length(B)
energy(i,:)=Zeeman(L,S,B(i));
end
plot(B,energy);
xlabel('Magnetic Field (T)');
ylabel('Energy Level');
title('Zeeman Splitting of L=1, S=1/2');
运行结果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号