队列是一种先进先出(First-In-First-Out,FIFO)的数据结构。队列被用在很多地方,比如提交操作系统执行的一系列进程、打印任务池等,一些仿真系统用队列来模拟银行或杂货店里排队的顾客。下面就介绍了Python中队列的应用实战,需要的可以参考。
队列(queue)
队列是先进先出(FIFO, First-In-First-Out)的线性表,在具体应用中通常用链表或者数组来实现,队列只允许在后端(称为rear)进行插入操作,在前端(称为front)进行删除操作,队列的操作方式和堆栈类似,唯一的区别在于队列只允许新数据在后端进行添加(摘录维基百科)。
如图所示
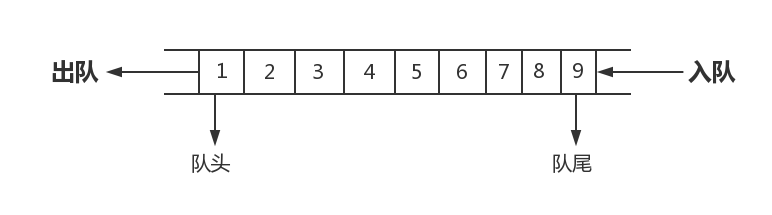
队列的接口
一个队列至少需要如下接口:
| 接口 | 描述 |
|---|
| add(x) |
入队 |
| delete() |
出队 |
| clear() |
清空队列 |
| isEmpty() |
判断队列是否为空 |
| isFull() |
判断队列是否未满 |
| length() |
队列的当前长度 |
| capability() |
队列的容量 |
然而在Python中,可以使用collections模块下的deque函数,deque函数提供了队列所有的接口,那么先让我门看看队列deque函数提供了那些API把:
collections.deque是双端队列,即左右两边都是可进可出的
| 方法 | 描述 |
|---|
| append(x) |
在队列的右边添加一个元素 |
| appendleft(x) |
在队列的左边添加一个元素 |
| clear() |
从队列中删除所有元素 |
| copy() |
返回一个浅拷贝的副本 |
| count(value) |
返回值在队列中出现的次数 |
| extend([x..]) |
使用可迭代的元素扩展队列的右侧 |
| extendleft([x..]) |
使用可迭代的元素扩展队列的右侧 |
| index(value, [start, [stop]]) |
返回值的第一个索引,如果值不存在,则引发ValueError。 |
| insert(index, object) |
在索引之前插入对象 |
| maxlen |
获取队列的最大长度 |
| pop() |
删除并返回最右侧的元素 |
| popleft() |
删除并返回最左侧的元素 |
| remove(value) |
删除查找到的第一个值 |
| reverse() |
队列中的所有元素进行翻转 |
| rotate() |
向右旋转队列n步(默认n = 1),如果n为负,向左旋转。 |
现在我们在Python中测试下这些个API的使用吧。
入队操作
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
>>> from collections import deque
>>> q = deque([1])
>>> q
deque([1])
>>> q.append(2)
>>> q
deque([1, 2])
>>> q.appendleft(3)
>>> q
deque([3, 1, 2])
>>> q.extend([4,5,6])
>>> q
deque([3, 1, 2, 4, 5, 6])
>>> q.extendleft([7,8,9])
>>> q
deque([9, 8, 7, 3, 1, 2, 4, 5, 6])
|
出队操作
|
1
2
3
4
5
6
7
8
9
10
|
>>> q.pop()
6
>>> q
deque([9, 8, 7, 3, 1, 2, 4, 5])
>>> q.popleft()
9
>>> q
deque([8, 7, 3, 1, 2, 4, 5])
|
其他的API
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
>>> q
deque([8, 7, 3, 1, 2, 4, 5])
>>> q.clear()
>>> q
deque([])
>>> not q
True
>>> q = deque([1,2], 10)
>>> q.maxlen
10
>>> q.extend([1,2,1,1])
>>> q.count(1)
4
>>> len(q)
6
>>> q.maxlen == len(q)
False
>>> q = deque([1,2,3,4,5],5)
>>> q.reverse()
>>> q
deque([5, 4, 3, 2, 1], maxlen=5)
>>> q.index(1)
4
>>> q
deque([5, 4, 3, 2, 1], maxlen=5)
>>> q.remove(5)
>>> q
deque([4, 3, 2, 1], maxlen=5)
>>> q
deque([4, 3, 2, 1], maxlen=5)
>>> q.rotate(2)
>>> q
deque([2, 1, 4, 3], maxlen=5)
>>> q.rotate(1)
>>> q
deque([3, 2, 1, 4], maxlen=5)
>>> q.rotate(-1)
>>> q
deque([2, 1, 4, 3], maxlen=5)
|
实例
二项式系数
题目
编写程序,求二项式系数表中(杨辉三角)第K层系列数
|
1
2
3
4
5
|
1
1 1
1 2 1
1 3 3 1
......
|
思路
- 把第K行的系数存储在队列中
- 依次出队K层的系数(每行最后一个1不出队),并推算K+1层系数,添加到队尾,最后在队尾添加一个1,便变成了k+1行。
解决代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
from collections import deque
def yanghui(k):
q = deque([1])
for i in range(k):
for _ in range(i):
q.append(q.popleft() + q[0])
q.append(1)
return list(q)
result = yanghui(3)
print(result)
|
划分无冲突子集
题目
某动物园搬家,要运走N种动物,老虎与狮子放在一起会大家,大象与犀牛放在一个笼子会打架,野猪和野狗放在一个笼子里会打架,现在需要我们设计一个算法,使得装进同一个笼子的动物互相不打架。
思路
- 把所有动物按次序入队
- 创建一个笼子(集合),出队一个动物,如果和笼子内动物无冲冲突则添加到该笼子,有冲突则添加到队尾,等待进入新笼子
- 由于队列先进先出的特性,如果当前出队动物的index不大于前一个出队动物的index,说明当前队列中所有动物已经尝试过进入且进入不了当前笼子,此时创建信的笼子(集合)
解决代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
from collections import deque
def division(m, n):
res = []
q = deque(range(n))
pre = n
while q:
cur = q.popleft()
if pre >= cur:
res.append([])
for a in res[-1]:
if m[cur][a]:
q.append(cur)
break
else:
res[-1].append(cur)
pre = cur
return res
N = 9
R = {
(1, 4), (4, 8), (1, 8), (1, 7),
(8, 3), (1, 0), (0, 5), (1, 5),
(3, 4), (5, 6), (5, 2), (6, 2), (6, 4),
}
M = [[0] * N for _ in range(N)]
for i, j in R:
M[i][j] = M[j][i] = 1
result = division(M, N)
print(result)
|
数字变换
题目
对于一对正整数a,b,对a只能进行加1,减1,乘2操作,问最少对a进行几次操作能得到b?
例如:
- a=3,b=11: 可以通过322-1,3次操作得到11;
- a=5,b=8:可以通过(5-1)*2,2次操作得到8;
思路
本题用广度优先搜索,寻找a到b状态迁移最短路径,对于每个状态s,可以转换到撞到s+1,s-1,s*2:
- 把初始化状态a入队;
- 出队一个状态s,然后s+1,s-1,s*2入队;
- 反复循环第二步骤,直到状态s为b;
解决代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
from collections import deque
def atob(a, b):
q = deque([(a, 0)])
checked = {a}
while True:
s, c = q.popleft()
if s == b:
break
if s < b:
if s + 1 not in checked:
q.append((s + 1, c + 1))
checked.add(s + 1)
if s * 2 not in checked:
q.append((s * 2, c + 1))
checked.add(s * 2)
if s > 0:
if s - 1 not in checked:
q.append((s - 1, c + 1))
checked.add(s - 1)
return q.popleft()[-1]
result = atob(3, 11)
print(result)
|
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作能带来一定的帮助,如果有疑问大家可以留言交流。
原文链接:http://www.h5min.cn/article/104517.htm




