洛谷 P2123 皇后游戏

前言

在 oi-wiki 的贪心部分下面看到的这题。当然，之前做国王游戏的时候就知道了这道题，但是在当时国王游戏就已经是极限难度了，所以并没有深究。下午看了这道题，用要写博客这件事逼着自己完全理解，结果似乎因为划水所以花了很长时间......

思路

首先，既然是皇后游戏，那么一定和国王游戏有联系（大胆猜测），考虑到国王游戏使用的是 邻项交换法，我们试着在这一题中也推出相应的式子。

不会 $\LaTeX$，故手写（

设当前相邻的两位为 $I，J$

第 $i$ 位大臣 左手上的硬币为 $l_i$ 右手为 $r_i$ 获得的硬币数量为 $v$

$I$ 的左右手分别为$a，b$；$J$ 的左右手分别为$c，d$

设 \sum_{i=1}^na_i，设 h = c_i-1

那么有

当 I 在前

 

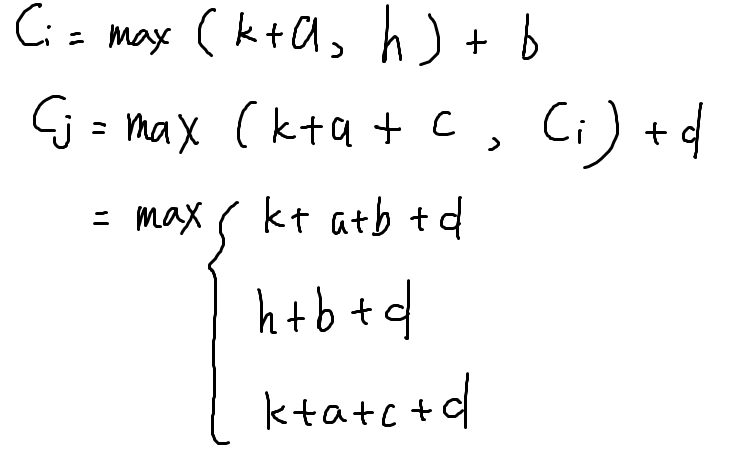
当 J 在前

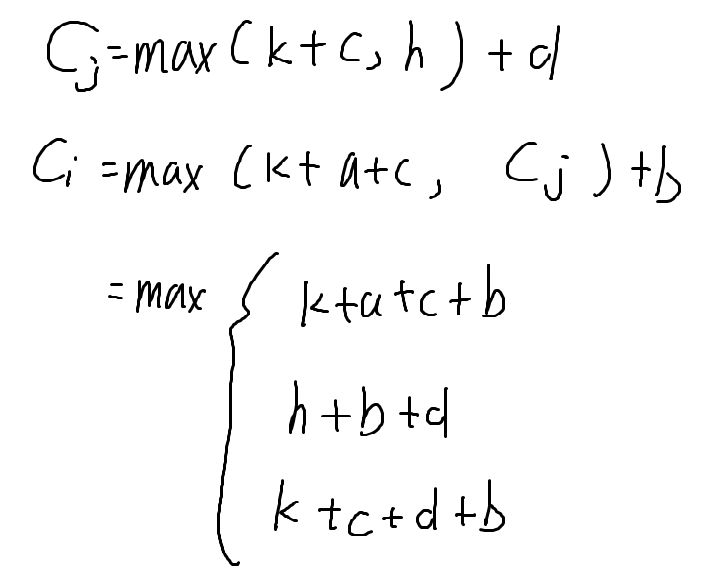
最后令 I，J 之中靠后的一方更小可以得到

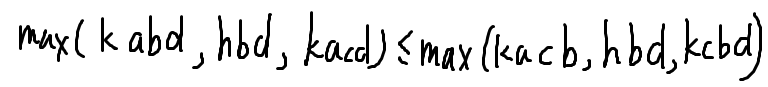
也就是说，只要满足这个式子，我们得到的解就是最优的。

但是很显然，两边都 hbd 这一项。可以考虑去掉，只考虑剩下两项。因为

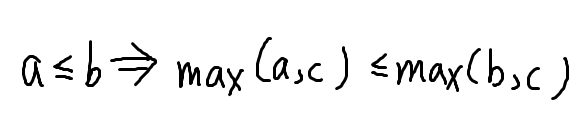
所以只要我们控制

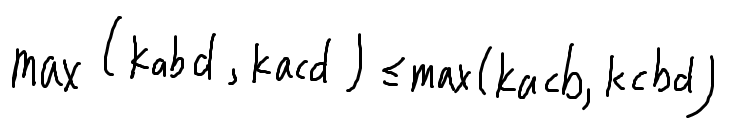
就可以满足上述式子，这个式子相当于一个充分条件。化简这个式子

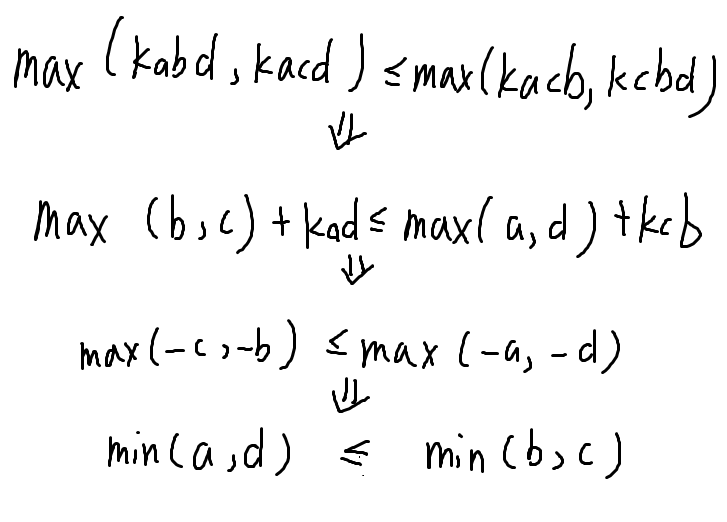
这样，这个式子中就只剩下和第 I，J 项有关的数据了。

然后，就像国王游戏那样，我们对所有大臣进行一个这样的排序，但是会发现，这样其实是不行的。很多题解都给出了一组 hack 数据，这里不做赘述，但是对于错误的原因要详细地说。

在对 I，J 进行比较的时候，我的定义是，如何让这两个大臣接在某个大臣之后，可以使得靠后的大臣价值更小。但是，不妨设想这样的一个场景。

在某个大臣后有三个大臣 A B C，此时他们的位置是 A B C。A 和 B 满足关系，B 和 C 满足关系，但是 A 和 C 不满足位置关系，也就是 C 应该在 A 的前面。使用 C++ 的 sort 之时，因为这种情况下相邻两项相相比都满足条件，程序便不再去改变这个序列，很容易导致错解。这要求我们设置的比较规则应该满足 传递性 这样，如果 A < B 且 B < C ，那么一定有 A < C，不会导致错解。

那么，我们思考一种方式，使得这种方式既有传递性，又可以满足上述式子 min(a,d)<=min(b,c)。

这里给出一种

将所有大臣分成三类，左手更小，左右手相同，右手更小，并且将这三种依此排列好。

对于同种大臣，左手更小的按照左手升序排列，右手更小的按照右手降序排列，左右手相同的随意排列。

容易证明，这样的比较方式具有传递性而且能满足上述式子（我是想不出来的）。

根据这样的方式 sort 一遍，然后按部就班求好答案就好了。

实现

看懂思路就可以直接上手写了。细节...似乎也不是很多，集中在排序上。

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline void read(int&x)
{
    x=0;bool f=1;
    char ch=getchar();
    while(ch<48||ch>57){f=!(ch==45);ch=getchar();}
    while(ch>=48&&ch<=57){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    x=f?x:-x;
}

int T;
struct node
{
    int l,r;
    bool operator<(const node x)const
    {
        if(l<r&&x.l>=x.r)return 1;
        if(l>r&&x.l<=x.r)return 0;
        
        if(l==r&&x.l<x.r)return 0;
        if(l==r&&x.l>x.r)return 1;
        
        if(l<r&&x.l<x.r)
        {
            return l<x.l;
        }
        if(l>r&&x.l>x.r)
        {
            return r>x.r;
        }
        if(l==r&&x.l==x.r)
        {
            return l<x.l;
        }
    }
}p[20001];

signed main(void)
{
    read(T);
    while(T--)
    {
        int n;read(n);
        for(register int i=1;i<=n;++i)
        {
            read(p[i].l);
            read(p[i].r);
        }
        sort(p+1,p+n+1);
        int ans=p[1].l+p[1].r;
        int tot=p[1].l;
        for(register int i=2;i<=n;++i)
        {
            tot+=p[i].l;
            ans=max(ans,max(tot,ans)+p[i].r);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

结语

　　对于邻项交换法的理解更深一层了。

Update 2021/8/21 将部分公式更换为 $\LaTeX$。