平衡三进制

前言

在 oiwiki 的进制位下面看到了平衡三进制。这是一种有趣的进制。因为 -1 的引入，把一个平衡三进制的所有数位上的数取相反数，就可以得到这个数的相反数。

介绍

普通的三进制书位上的数可以是0，1，2，而平衡三进制则是1，0，-1，下文用 Z 来表示 -1。

转化成十进制的计算方法和其他进位制是一样的，∑a_i*3^i-1，而十进制转化为平衡三进制，则需要先转化为普通三进制，然后按照如下步骤从低位到高位操作。

1，遇到 0 和 1，直接跳过

2，遇到 2，当前位改为 Z，下一位 +1

3，遇到 3，当前位改为 0，下一位 +1

讨论

显然，按照这样的操作步骤，一个十进制能且仅能得到一个平衡三进制数。但是，是否存在两个不同的平衡三进制数，使得这两个数可以转化为同一个十进制数呢？

不妨设有两个平衡三进制数 A B。

A 的 第 i 位为 a_i，B 的第 i 位为 b_i

显然，A 和 B 不同，当且仅当存在一个 i，使得 a_i ≠ b_i 

 

显然，1*3^i-1 > ∑2*3^i-2

显然，1*3ⁱ > 2*3^i-1

于是，也就是说，如果第 i 位不同，单靠 1 -> i-1 这些位上的数字不能与之抵消（太小了），单靠 i+1 及以上的位数也不能与之抵消（太大了）。

于是考虑结合起来，使得 i 左右两边对第 i 位的影响尽量接近于 1^3^i-1 或者 2^3^i-1 。

先取一个 1^3^i-1 发现过大，考虑用低位减小，越小越好，于是取 ∑2*3^i-2 。

可以发现，最后得到的结果， 1^3^i-1 -  ∑2*3^i-2 =  2^3^i-1 ^ 1。还是太大了。

以上过程有些抽象，这里有一个图示

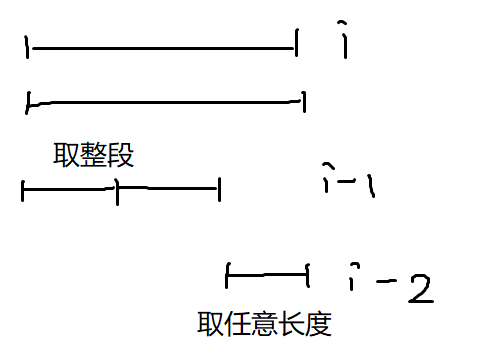
显然，图中的 3ⁱ 和 3^i-2 不肯能组合出为 1^3^i-1 或 2^3^i-1 

也就是说，当 a_i ≠ b_i 不可能通过其他位数的改变弥补 a_i - b_i ，使得 A = B。

也就是说，当 A ≠ B，A 和 B转化成的十进制数不可能相等。

延伸

既然有平衡三进制，是否平衡四进制？（平衡二进制怎么做？如果使用 0 和 -1，就和二进制没有本质上的区别的，还是需要符号位来进行符号的判断，因此不讨论）

平衡四进制怎么分配？或许是1，0，-1，-2，或许是2，1，0，-1。

以1，0，-1，-2 来考虑。用 Z 代表 -1，用 Ｔ 代表 -２。

仿照平衡三进制，既然要使得位数都再 1，0，-1，-2 之间，因此在四进制中

遇到4，令当前位为0，下一位+1

遇到 3，令当前位为 -1，下一位+1

遇到 2，令当前位 为-2，下一位+1

遇到 1，0，直接跳过

按照这个规则

试着转化79

转化为四进制 1033

按步骤操作 104Z 110Z

 试着转化 103

转化为四进制　1213

按步骤操作 102Z 11TZ

可见平衡四进制是可以实现的！

吗？

我们会发现，平衡四进制表示的数域中，正数域和负数域不对应。而且，也不能对每个数进行取相反数的操作。如果我们选用 1，0，-1，-2，那么范围就是 -42->21。那么，得到 22->42 的数字就有两种方法。第一种，把 -42 -> -22 的 平衡四进制数 的 所有位数上的数字 取相反数，或者进到更高的位数来表示。可见平衡四进制并不“平衡”，它数域不对称，而且和十进制不是一一映射。

相比之下，平衡五进制则更为简单，更为对称，更为美观，只需要在 平衡三进制的基础上加上 -2 和 2 即可。运算方法也很好推：

遇 5 化 0，下位 +1

遇 4 化 Z，下位 +1

遇 3 化 T，下位 +1

遇到0，1，2直接跳过

显然平衡五进制和十进制一一对应，而且数域对称，网上也有相关的资料。

百度百科平衡五进制 https://baike.baidu.com/item/%E5%B9%B3%E8%A1%A1%E4%BA%94%E8%BF%9B%E5%88%B6/53359940?fr=aladdin

思考

平衡进制和普通进制有什么区别？我们可以发现，位数相同的 n 进制数，可以表示的数字的集合大小是一样的。

比如三位数的三进制和平衡三进制，三进制的范围是 0->26，平衡三进制的范围是 -13->13，集合元素个数均为 27 个。

只有当 n 是奇数的时候，我们可以构造出美丽的平衡 n 进制。

三进制还有什么优秀的性质？还有什么应用场景？或许它可以改变世界，又或许它只是一个有趣的数学游戏。而这一切都充满未知。