图论杂题
Codeforces 1572 D - Bridge Club
题意
给出 \(n\)，有 \(2^n\) 个点，点权已给出。要求只有两个点的编号的二进制上有且只有一个位置不同时，这两个点有连边。求原图最多选择 \(k\) 条边的最大（点）权匹配。
\(n\le 20;k\le 100\)
Sol
考虑边连接的两个点的 \(\mathrm{popcount}\) 一定不同，因此原图是二分图。
考虑网络流可以解决这个问题。
但是原图的边数达到了惊人的 \(n2^n\) 条，所以肯定是不能做的。
把两个点的点权放在边上。
每次选择一条边，最多导致 \(2n-2\) 条边无法选择。因此选择前 \(2nk\) 大的边，跑费用流即可。
UniversalOJ #461 - 新年的Dog划分
题意
交互题。
给定 \(n\)，有一个 \(n\) 个点的二分图，每次你可以给出一个点对集，若点对之间有边则会将其删去，返回一个布尔值表示原图删去这些边后是否联通。
你需要输出二分图的一个部分，或者判断原图不为二分图。
\(n\le 200\)，询问次数不超过 \(2000\)。
Sol
task 1. 考虑如何确定一条边？
这条边 \(e\) 存在等价于存在一个边集 \(S\)，满足 \(e\notin S\)，只有 \(S\) 中的边时原图不联通，加上 \(e\) 后联通
task 2. 考虑一个可以高效解决联通问题和二分图染色的结构。
树。
task 3. 结合前两个 task。
考虑二分，将所有点对（无论是否真的存在边）排在一起，考虑保留 \(e_1,\cdots,e_i\) 时图联通，保留 \(e_1,\cdots,e_{i-1}\) 时不联通，则 \(e_i\) 在图中。下次二分时保留 \(e_1,\cdots,e_{j},e_i\) 可联通，保留 \(e_1,\cdots,e_{j-1},e_i\) 不连通，可以得到 \(e_j\)。
这样只能做 \(n-1\) 次，之后会得到原图的一颗生成树，这样我们就可以划分出二分图的两个部分。
task 4. 已知两个部分和生成树，判断是否为二分图。
只保留同色点的边，以及生成树上的边。如果存在一个生成树上的边使得断开后原图依然联通，那么原图不是二分图。否则原图是二分图。
task 5. 考虑 task 3. 中的二分是在 \(\frac{n(n-1)}{2}\) 条上进行的，次数应该是 \(2\log_2 n\)，实际上乘上 \(n\) 是会超次数的，因此我们考虑将这些边的排列分块，每块量级为 \(O(n)\)，这样因为我们顺次选出的 \(e_i,e_j,e_k,\cdots\) 应该满足 \(i>j>k>\cdots\)，因此可以在块内二分，这样次数就是 \(n\log_2n+O(n)\)，能够通过此题。
Luogu P3679 - [CERC2016] 二分毯 Bipartite Blanket
题意
给出一个二分图，二分图的左部有 \(n\) 个点，右部有 \(m\) 个点，每个点有权值。求有多少个点集，权值和大于等于 \(t\)，且满足存在覆盖可以完全包含这些点。
\(n,m\le 20\)
Sol
对于某个覆盖 \(M\)，准确说它是一个边集，我们用 \(v(M)\) 来表示它关联的点集。
一般的 Hall 定理做这题时间复杂度高达 \(O(3^{n})\)，舍去。
广义 Hall 定理：对于一个原图的点集 \(V\)，设它在右部的点集为 \(X\)，在左部的点集为 \(Y\)。
则有：
证明
考虑点集包含 \(X\) 的最大覆盖（不一定完美，但一定极大） \(M_X\)，和定义同理的 \(M_Y\)。记 \(M=M_X\cup M_Y\)。
只考虑 \(M\) 中的边的话，原图所有点的度数均小于等于 \(2\)，因此只可能存在独立环和独立链。
对于环，因为是二分图，所以一定是偶环，直接隔一条边选一条即可。
对于链，如果是奇数条边，那么隔一条边选一条；如果是偶数条边，会发现连接多点的边只可能是 \(M_X\) 或 \(M_Y\) 其中一个里边的，因此它的端点两边的两点一定不会都是 \(X\cup Y\) 中的点，因此可以不管它。
\(\Box\)
因此，我们对于左部图和右部图分别判断是否合法，然后排序后用双指针做就可以了。
时间复杂度 \(O(n2^n)\)。
// Not afraid to dark.
#include <bits/stdc++.h>
using namespace std;
#define int long long
namespace io {
int read_pos, read_dt; char read_char;
inline int read (int &p = read_pos){
p = 0, read_dt = 1; read_char = getchar ();
while (! isdigit (read_char)){
if (read_char == '-')
read_dt = - 1;
read_char = getchar ();
}
while (isdigit (read_char)){
p = (p << 1) + (p << 3) + read_char - 48;
read_char = getchar ();
}
return p = p * read_dt;
}
int write_sta[65], write_top;
inline void write (int x){
if (x < 0)
putchar ('-'), x = - x;
write_top = 0;
do
write_sta[write_top ++] = x % 10, x /= 10;
while (x);
while (write_top)
putchar (write_sta[-- write_top] + 48);
}
}
#define popcount(x) (__builtin_popcount (x))
#define lowbit(x) ((x) & (- (x)))
const int N = 20;
int n, m, t;
int vn[N], vm[N], cn[N], cm[N];
char ins[N + 5][N + 5];
int cntn, cntm;
int nS[1 << N], mS[1 << N];
bool f[1 << N];
signed main (){
io::read (n), io::read (m);
for (int i = 0;i < n;++ i)
scanf ("\n%s", ins[i]);
for (int i = 0;i < n;++ i)
io::read (cn[i]);
for (int i = 0;i < m;++ i)
io::read (cm[i]);
io::read (t);
for (int i = 0;i < n;++ i)
for (int j = 0;j < m;++ j)
vn[i] |= (ins[i][j] - '0') << j;
for (int i = 0;i < m;++ i)
for (int j = 0;j < n;++ j)
vm[i] |= (ins[j][i] - '0') << j;
f[0] = true;
cntn = 1;
for (int i = 1;i < (1 << n);++ i){
f[i] = true;
int vt = 0;
for (int j = 0;j < n;++ j)
if (i >> j & 1){
vt |= vn[j];
f[i] = (f[i] && f[i ^ (1 << j)]);
}
f[i] = (f[i] && popcount (vt) >= popcount (i));
if (f[i]){
int val = 0;
for (int j = 0;j < n;++ j)
if (i >> j & 1)
val += cn[j];
nS[cntn ++] = val;
}
}
cntm = 1;
for (int i = 1;i < (1 << m);++ i){
f[i] = true;
int vt = 0;
for (int j = 0;j < m;++ j)
if (i >> j & 1){
vt |= vm[j];
f[i] = (f[i] && f[i ^ (1 << j)]);
}
f[i] = (f[i] && popcount (vt) >= popcount (i));
if (f[i]){
int val = 0;
for (int j = 0;j < m;++ j)
if (i >> j & 1)
val += cm[j];
mS[cntm ++] = val;
}
}
sort (nS, nS + cntn);
sort (mS, mS + cntm);
int ans = 0;
for (int i = 0, j = cntm;i < cntn;++ i){
while (j && nS[i] + mS[j - 1] >= t)
-- j;
ans += cntm - j;
}
io::write (ans), puts ("");
return 0;
}
QOJ #6508 - This is not an Abnormal Team!
题意
现在有一个二分图，左部有 \(n_1\) 个点，右部有 \(n_2\) 个点，共 \(m\) 条边。你需要将其划分成多个子图，使得每个子图的点数不超过 \(3\)，且均为链。要求点数为 \(1\) 的子图尽量小，并且在此前提下点数为 \(3\) 的子图尽量小。
\(n_1,n_2\le10^5;m\le2\times 10^5\)
Sol
考虑我们一定是先做这个二分图的最大匹配，然后将尽量多的单点合并进已匹配的边里，最后一定是能够在最小化单点的情况下最小化三点链。
最大匹配是简单的，但是合并时 \(LRL\) 的合并应该和 \(RLR\) 的合并分开处理，因此跑三遍最大流即可。
证明考虑演绎一下不同的情况就可以了。
Codeforces 1383 F - Special Edges
题意
给出一个 \(n\) 个点 \(m\) 条边的流网络，每条边的容量均小于等于 \(25\)。
其中前 \(k\) 条边为特殊边，初始没有给出流量。现在有 \(q\) 个询问，每个询问给出前 \(k\) 条边的容量，要你求出这个图的最大流。
\(n,m\le 10^4;k\le 10;q\le 2\times 10^5\)。
Sol
考虑最大流最小割定理，我们考虑前 \(k\) 个点的选择情况，共有 \(2^k\) 种不同的情况，枚举割不割这条边。会发现最后询问时对把割掉的边的价值加上，我们可以在 \(O(q2^k)\) 时间复杂度内解决这个问题。
但是我们直接枚举 \(2^k\) 跑 \(\textrm{Dinic}\) 肯定寄了。但是发现容量很小。
因此我们考虑初始其他边时跑一边 \(\textrm{Dinic}\)， \(i\) 在 \(i-\mathrm{lowbit}(i)\) 的残量网络上加新边跑 \(\mathrm{FF}\)。因为 \(\textrm{FF}\) 的时间复杂度上界为 \(O(|E|\Delta f)\)，因此我们会得到一个时间复杂度 \(O(2^km\cdot w)\)，其中 \(w\) 为每条边容量上界，最多为 \(25\)。
Atcoder ARC 107 F - Sum of Abs
题意
一个 \(n\) 个点 \(m\) 条边的无向图。你可以花费 \(A_i\) 的代价删去第 \(i\) 个点以及相连的边。在删除完成后，无向图的价值定义为每个极大连通块的权值之和，每个极大连通块的权值是其中所有点的 \(B_i\) 之和的绝对值。
这时你的收益为无向图删除完成后的价值减去删除花费的代价。
求最大收益。
\(n,m\le 300;|A_i|,|B_i|\le 10^6\)。
Sol
如果每个点都能按照自己的需求取正负，那么最后的目标收益是 \(\sum |B_i|\)。
但是因为连通关系，所以这个是不一定取得到的。
因此每个点有三种状态：
- 被删去。这会让收益减少 \(A_i+|B_i|\)。
- 它所在的连通块最终直接取和。如果 \(B_i<0\)，这会让收益减少 \(2|B_i|\)。
- 它所在的连通块最终取和的相反数。如果 \(B_i>0\)，这会让收益减少 \(2|B_i|\)。
我们要让收益从目标收益开始减去最小的代价得到最大收益，同时将每个点划分到不同的状态中。
考虑最小割解决这个问题。
设 \(s\) 相连的是取和，\(t\) 相连的是取相反数。
-
对于每个点拆出 \(u_{\mathrm{in}}\) 和 \(u_{\mathrm{out}}\) 两个点，在中间连上 \(A_i+|B_i|\)。
-
如果 \(B_i<0\)，那么应该有 \((u_{\mathrm{out}}, t, 2|B_i|)\)。
-
如果 \(B_i>0\)，那么应该有 \((s,u_{\mathrm{in}},2|B_i|)\)。
然后因为边的连通的性质，如果一个点状态是取正，那么所有和它有连边且没被删去的点应该也是取正的，所以在边上要考虑约束取正（也相当于约束取负）。
因此我们我们对于一条边 \((u,v)\)，在流网络中加入 \((u_{\mathrm{out}},v_{\mathrm{in}}, \infty), (v_{\mathrm{out}},u_{\mathrm{in}}, \infty)\)。
这些边只会在两个点均没被删去时产生约束作用，因此完全正确。
Gym 104869 A - Intro: Dawn of a New Era
题意
给出 \(n\) 个集合 \(S_1 \cdots S_n\)。
现在你需要给出一种排列方式，使得：
的值最大。其中 \([]\) 是艾佛森括号。
\(n\le 10^5;\sum |S_i|\le 2\times 10^5\)。
Sol
会做就行了。
考虑把和式中的条件看作能否连在一起的条件看作能否连在一起的关系，因此题目中的和式应该等于 \(n\) 减去连在一起的块的数量。
因此我们要让连在一起的块的数量最小。
考虑构建一个图，把集合内元素看作点。对于一个集合，将非最大值的点连向最大值的点。
所以我们实际要做一个最小路径覆盖问题：任意集合的最大值一定被经过，且保证同一个集合对应的边至多有一条边被覆盖。
因此使用网络流算法。
因此我们把每个元素拆成入点和出点，如果元素是某个集合的最大值，则流量至少为 \(1\)，同时给每个集合分配一个点，用以限制这个集合的点连向最大值的流量至多为 \(1\)（就是这些点连向集合代表的点，再由集合代表的点连向最大值的点）。
最后源点向所有集合代表的点连边，跑上下界最小流即可。
同时发现会有一些集合没有被覆盖，我们考虑把它放在和它最大值相同的集合后面，就可以在不增加连接在一起的块数地情况下解决了（不可能不存在和它最大值相同的集合，否则它代表的最大值一定会被相应地覆盖掉）。
LibreOJ #3461 - Paint by Letters
题意
现在有一个 \(n\times m\) 的目标颜色矩阵。一笔可以将一个目标颜色相同的连通块全部染成目标颜色。
现在给出 \(q\) 个询问，每次给定一个子矩阵，问只染色这个子矩阵至少需要多少笔。
\(n,m,q\le 1000\)。
Sol
给相邻同色格子连边，我们相当于要求一个以子矩阵中所有点的导出子图的连通块个数，而且这个图是平面图。
首先，设这个图的点集为 \(V\)，边集为 \(E\)，划分出了 \(R\) 个区域（包含最外层的无限面积的区域），有 \(C\) 个连通块，则有欧拉平面图定理：
证明考虑归纳法：
- 一个点时显然成立。
- 在一个图中加入一个新的点：\(|V|\leftarrow |V| + 1,|C|\leftarrow |C| + 1\)。
- 在一个图中加入一个边和一个点，其中边的一个顶点是新加入的点：\(|V|\leftarrow|V|+1,|E|\leftarrow|E|+1\)。
- 在一个图中连接两个在同一连通块内的点：\(|E|\leftarrow |E+1|,|R|\leftarrow|R|+1\)。
可以归纳出所有平面图的情况。
因此我们需要找到子矩阵的导出子图中的点数、边数以及区域数。
前两个使用二维前缀和，总是好做的。
重点应该是考虑区域数。因为网格图具有特殊性，所以我们可以选择用下图中行黑线和列黑线交叉的十字位置当做区域的最小单位格。
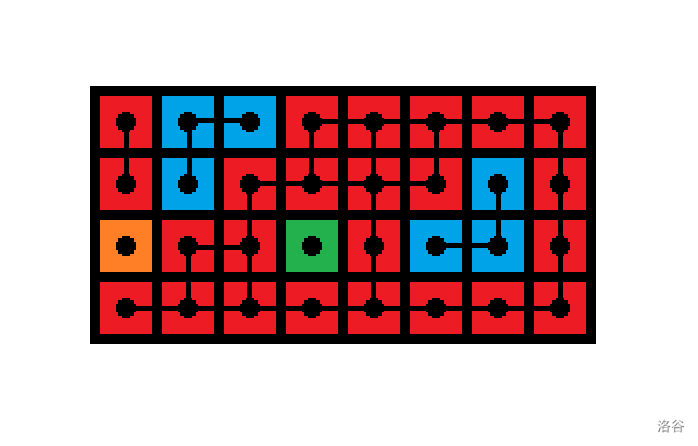
我们可以给这些十字编号 \((0,0)\) 到 \((n,m)\)。然后做染色，给同一片区域染同一个颜色，然后在这个区域内定一个特殊位置。
然后对这个特殊位置的个数做二维前缀和。
在子矩阵计算时我们把 \([x_1,x_2-1][y_1,y_2-1]\) 的十字上的特殊位置个数加起来。之后遍历这个子矩阵的外围，如果某个十字的区域的特殊位置在我们计数的范围之内，我们就把他丢掉，答案减一。注意一个特殊位置只能被丢掉一次，所以要用 \(\textrm{unordered map}\) 之类的去重。
答案就是 \(|V|-|E|+R-1\)。
时间复杂度 \(O(nm+q(n+m))\)。
UniversalOJ #733 - [JOISC2022] 复兴计划
题意
给定 \(n\) 个顶点和 \(m\) 条边，每条边一个有系数 \(w_i\)。
现在给出 \(q\) 个询问，每个询问给出一个值 \(x\)，让你求出一个构成生成树的边集 \(E\)，使得：
最小。
\(n\le 500;m\le 10^5;q\le 10^6;w_i,x\le 10^9\)。
Sol
考虑存在这样一个结论：对于正整数域上的所有 \(x\) 取值，某条边 \(e\) 出现的范围一定是一个区间 \([l_e,r_e]\)。
考虑 \(|w_e-x|\) 这样一个函数是一个触底反弹的斜率绝对值为 \(1\) 的函数。对于这种函数，要么相等，要么只有一个交点。
而考虑我们求的最小生成树，实际上是在 \(x\) 处做与 \(y\) 轴平行的线，然后从下往上加边（如果两顶点不连通的话），知道全部点连通。
所以如果 \(e\) 被某条边取代了，它一定不会再取代某个其他边。
\(\Box\)
因此考虑按 \(w\) 从大到小排序后遍历一遍，每次枚举到当前边 \(e\)，则在当前最小生成树上找 \(u,v\) 之间的链。
- 如果没找到，说明还没构成最小生成树，直接加入即可。
- 否则，因为我们从大到小遍历，所以在这个链中所有边的花费在 \(x=w_e\) 时比 \(e\) 大，因此考虑删去一条花费最大的 \(e'\)。相当于是 \(e\) 替换了 \(e'\)。
最后，会发现在 \(x\le \lfloor \frac{w_e+w_{e'}}{2}\rfloor\) 时选择 \(e\) 更优，因此有：
实际上如果有相同的 \(w_e\) 同样是正确的。
最后询问时，询问了 \(x\) 相当于是问
差分或者简单数据结构维护即可。
