【题解】 「NOI2020」超现实树 trie树+dp+结论题 LOJ3343
超现实树
感觉这个题非常牛逼，来纪念一下。
Link \(\textrm{to LOJ}\)。
Editorial
遇到这种神仙题，我们肯定要观察一下规律对吧？通常出题人会设置一些比较好找规律的部分分！
性质 1
树高不超过 2。
这种情况下只有两包含以下两种子集的树的集合有解：
_
{_}
或
_ _ _
{_} {_} {_}
/ \ / \
_/ \_ + _/ + \_
{_} {_} {_} {_}
第一种情况显然从一个结点可以长出所有的树。
第二种情况除了一个结点的树无法生长的得到，其它都可以。
性质 2
给出的树高度相同。
不会啊。
性质 3
树的集合仅包含链。
不难发现，除了存在单个结点时有解，否则无解。
因为一定无法长出形如：
_
{_}
/ \
_/ \_
{_} {_}
的树，和它可以长出的树。
性质 4
性质 2 是性质 4 的真子集。
也就是把性质二的三种树结构的上方加了一条链。
由性质二的第二种合法情况可以启发我们。
猜测一下是不是所有这样的三个结构同时出现就可以等价地把它缩成一个结点？
比如：
_ _ _ _ _
{_} {_} {_} {_} {_}
/ / / \ / \
_/ _/ _/ \_ _/ \_
{_} + {_} + {_} + {_} + {_} {_}
/ \ / \
_/ \_ _/ \_
{_} {_} {_} {_}
| |
V V
_ _ _
{_} {_} {_}
/ \ / \
_/ + \_ + _/ \_
{_} {_} {_} {_}
| |
V V
_
{_}
好像成立的样子？
那么这个呢？
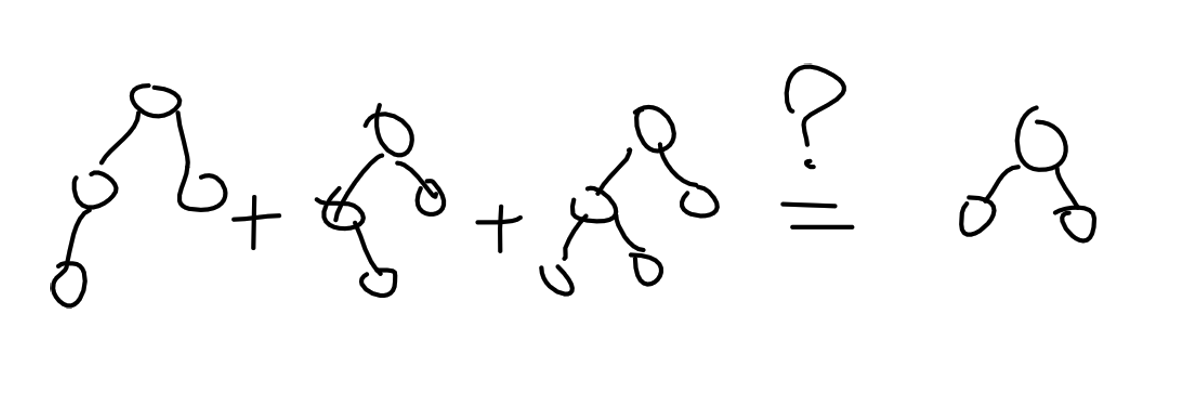
事实上并不能等价，因为形如：
_
{_}
/ \
_/ \_
{_} {_}
/ \
/ ... \
/_______\
的树，用左边的组合是搞不出来的，但用右侧的一棵树是可以做到的。
不过你实现这个做法，交上去就有 16 分了（
不妨按照这种思路想下去，我们把左边的树对称一下加进集合，这样可以构成所有树了吗？
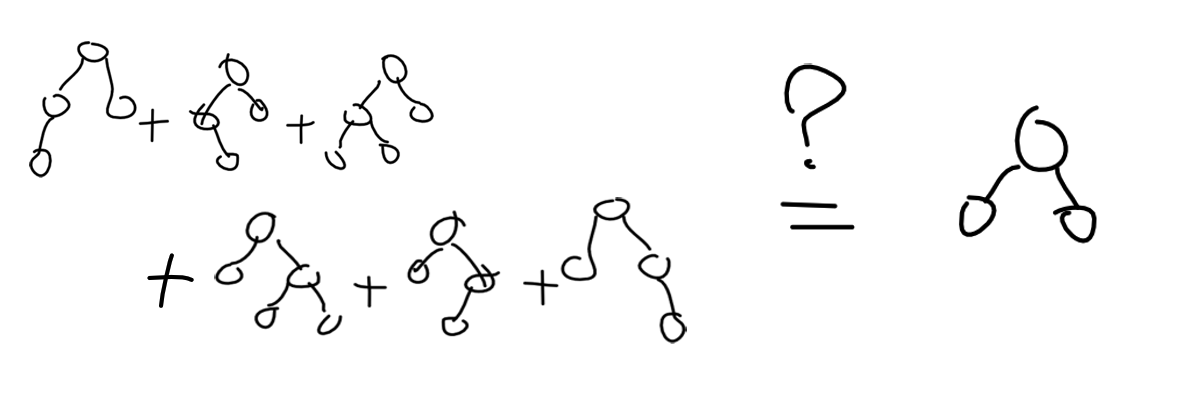
是可以的！上文提到的不能形成的树恰好可以被新加入的三棵树的组合完美解决！
于是我们就可以做性质 4 了，我们对于每个结点都检查能不能把子树内的全部解决掉，然后向上树形 dp 就行了。
正解
出题人给性质 4 一定别有用心，ta 为什么只给了链状和 Y 状树呢？
如果玩一下其他的树，会有神奇的事情发生：因为所有孩子数量大于 2 的结点，必然有一个是叶子，否则这棵树不会起到任何作用！
原因么……
_
{_}
/ \
_/ \_
{_} {_}
/ \
/ ... \
/_______\
当然是因为无论怎么组合，这样的树都是搞不出来的啦。
严谨证明应该要数学归纳
或者用出题人所说的机器辅助形式化证明
于是我们把不合法的树先全部去掉，然后运行性质 4 的算法就可以了！
Code
#include <bits/stdc++.h>
#define debug(...) fprintf(stderr ,__VA_ARGS__)
#define LL long long
#define __FILE(x)\
freopen(#x".in" ,"r" ,stdin);\
freopen(#x".out" ,"w" ,stdout)
int read(){
char k = getchar(); int x = 0;
while(k < '0' || k > '9') k = getchar();
while(k >= '0' && k <= '9') x = x * 10 + k - '0' ,k = getchar();
return x;
}
const int MX_N = 2e6 + 23;
int m;
int ch[MX_N][2] ,sz[MX_N];
bool check(int x){
if(!x) return true;
if(!check(ch[x][0]) || !check(ch[x][1])) return false;
if(sz[ch[x][0]] > 1 && sz[ch[x][1]] > 1) return false;
sz[x] = 1 + sz[ch[x][0]] + sz[ch[x][1]];
return true;
}
int tot = 1;
int trie[MX_N][4] ,status[MX_N];
// status = 1 ,2 ,4 分别代表 / + \ + /\ 这类子树能不能长出来
void insert(int x ,int y){
if(sz[y] == 2){
if(ch[y][0]) status[x] |= 1;
if(ch[y][1]) status[x] |= 2;
return;
}
if(sz[y] == 3 && ch[y][0] && ch[y][1]){
status[x] |= 4;
return;
}
int to = sz[ch[y][0]] <= 1;
int rt = to + (sz[ch[y][!to]] << 1);
if(!trie[x][rt]) trie[x][rt] = ++tot;
insert(trie[x][rt] ,ch[y][to]);
}
int ok;
void getit(int x){
if(!x) return;
getit(trie[x][0]);
getit(trie[x][1]);
getit(trie[x][2]);
getit(trie[x][3]);
if(status[trie[x][0]] == 7) status[x] |= 1;
if(status[trie[x][1]] == 7) status[x] |= 2;
if(status[trie[x][2]] == 7
&& status[trie[x][3]] == 7) status[x] |= 4;
debug("status[%d] = %d\n" ,x ,status[x]);
}
void solve(){
m = read();
for(int t = 1 ; t <= m ; ++t){
int n = read();
for(int i = 1 ; i <= n ; ++i){
ch[i][0] = read();
ch[i][1] = read();
}
if(n == 1) ok = 1;
if(ok) continue;
if(check(1)){
insert(1 ,1);
}
}
if(!ok){
getit(1);
if(status[1] == 7) ok = 1;
else ok = -1;
}
puts(ok >= 0 ? "Almost Complete" : "No");
for(int i = 1 ; i <= tot ; ++i){
memset(trie[i] ,0 ,sizeof trie[0]);
status[i] = 0;
}
tot = 1;
ok = 0;
}
int main(){
__FILE(surreal);
int T = read();
while(T--) solve();
return 0;
}
