【题解】 CF1419F Rain of Fire 并查集+二分答案+暴力
Legend
Link \(\textrm{to Codeforces}\)。
给定 \(n\ (1 \le n \le 1000)\) 个二维平面上的点,坐标 \((x_i,y_i)\ (|x_i|,|y_i| \le 10^9)\)。
两个点 \(i,j\) 可以互相到达当且仅当他们 \(x_i=x_j\) 或者 \(y_i=y_j\)。
发现有的情况所有点可能到不了,于是你可以在任意位置设置至多 1 个新点。
同时每隔 \(t\) 秒会有一次轰炸,意思是两个点 \(i,j\) 可以互相到达还要它们之间的距离 \(\le t\)。
求出最小的 \(t\),使得所有点可以相互到达,到不了请输出 \(-1\)。
Editorial
有显然的可二分性,二分一个 \(t=mid\),然后考虑怎么 \(\rm{check}\) 是否可行。
先不考虑新加点。
\(n\) 很小,让人想到暴力并查集。得到了若干个连通块。
此时考虑新加点。
发现显然连通块个数 \(>4\) 的时候即使加入新点也永远无法连通。
那么对于连通块个数分类讨论一下即可。
连通块个数 \(=1\)
可行。
连通块个数 \(=2\)
暴力枚举不同连通块的两个点 \(i,j\):
- 如果不在同一行或者同一列,看是不是 \(\max(|x_i-x_j|,|y_i-y_j|) \ge mid\),是就可行;
- 如果在同一行或者同一列,看是不是距离 \(\le 2mid\),是就可行。
如果不存在上述两种点对,则不可行。
此部分复杂度 \(O(n^2)\)。
连通块个数 \(=3\)
一定存在一个点使得它到三个连通块的距离都 \(\le mid\)。
设所有的连通块是 \(X,Y,Z\)。
枚举两个连通块 \(X,Y\),看看哪些点是可能潜在的新点,最多只有 \(O(n^2)\) 个。
再枚举 \(X,Z\),看看哪些点是可能潜在的新点且与之前 \(X,Y\) 的潜在的新点重合,如果有重合那么就可行。
那么什么是潜在的新点呢?比如对于下面这个三个点的图:
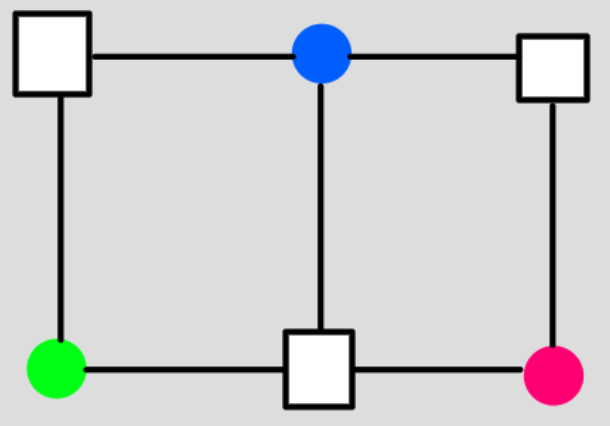
白色的矩形位置都是潜在的新点,但是只有中排的这个白色矩形才是“粉蓝”,“绿蓝”两组连通块共同的潜在的新点,于是就可以放在这里。
如果我们此时恰好枚举到的是 \(X=蓝,Y=粉,Z=绿\),那么就很幸运的做完了。
但如果不幸枚举到 了\(X=粉,Y=蓝,Z=绿\),那么“粉蓝”,“粉绿”两组连通块就没有找到共同的潜在的新点。
如果没有就轮换 \(X,Y,Z\) 再做,直到 \(3\) 种情况都试完了为止,此时一定不行。
此部分复杂度 \(O(n^2)\)。
连通块个数 \(=4\)
一定存在一个点使得它到四个连通块的距离都 \(\le mid\)。
设所有的连通块是 \(A,B,C,D\)。
跟三个连通块同理,也只要找两个集合枚举潜在的新点,拿另外两个集合检查即可。
只要测试 \(2\) 轮。
此部分复杂度 \(O(n^2)\)。
所以加上二分总复杂度 \(O(n^2 \log x)\)。
Code
丑陋无比……
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int MX = 1000 + 233;
int n;
unordered_map<LL ,int> lshx ,lshy;
struct point{
LL x ,y;
LL mxd(point b){
return max(abs(x - b.x) ,abs(y - b.y));
}
}p[MX];
int fa[MX] ,vis[MX] ,lead[MX];
int tag[MX][MX] ,tc;
void init(){
for(int i = 1 ; i <= n ; ++i)
fa[i] = i ,vis[i] = 0;
}
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}
LL X[MX] ,Y[MX];
bool check(LL len){
init();
for(int i = 1 ; i <= n ; ++i){
for(int j = i + 1 ; j <= n ; ++j){
if(p[i].x == p[j].x){
if(abs(p[i].y - p[j].y) <= len){
fa[find(i)] = find(j);
}
}
if(p[i].y == p[j].y){
if(abs(p[i].x - p[j].x) <= len){
fa[find(i)] = find(j);
}
}
}
}
int ltk = 0;
for(int i = 1 ; i <= n ; ++i){
if(!vis[find(i)]){
vis[find(i)] = ++ltk;
lead[ltk] = find(i);
}
}
if(ltk == 1) return true;
if(ltk == 2){
LL dis = LLONG_MAX;
for(int i = 1 ; i <= n ; ++i){
if(find(i) != lead[1]) continue;
for(int j = 1 ; j <= n ; ++j){
if(find(j) != lead[2]) continue;
if(p[i].x == p[j].x){
dis = min(dis ,(abs(p[i].y - p[j].y) + 1) / 2);
}
else if(p[i].y == p[j].y){
dis = min(dis ,(abs(p[i].x - p[j].x) + 1) / 2);
}
else dis = min(dis ,p[i].mxd(p[j]));
}
}
return dis <= len;
}
if(ltk == 3){
int qwq[4] = {0 ,1 ,2 ,3};
for(int T = 1 ; T <= 3 ; ++T){
++tc;
swap(qwq[1] ,qwq[T]);
for(int i = 1 ; i <= n ; ++i){
if(find(i) != lead[qwq[1]]) continue;
for(int j = 1 ; j <= n ; ++j){
if(find(j) != lead[qwq[2]]) continue;
if(p[i].mxd(p[j]) <= len){
tag[lshx[p[i].x]][lshy[p[j].y]] = tc;
tag[lshx[p[j].x]][lshy[p[i].y]] = tc;
}
}
}
for(int i = 1 ; i <= n ; ++i){
if(find(i) != lead[qwq[1]]) continue;
for(int j = 1 ; j <= n ; ++j){
if(find(j) != lead[qwq[3]]) continue;
if(p[i].mxd(p[j]) <= len){
if(p[i].mxd(p[j]) <= len &&
(tag[lshx[p[i].x]][lshy[p[j].y]] == tc
|| tag[lshx[p[j].x]][lshy[p[i].y]] == tc))
return 1;
}
}
}
}
return false;
}
if(ltk == 4){
int qwq[5] = {0 ,1 ,2 ,3 ,4};
for(int T = 1 ; T <= 2 ; ++T){
++tc;
swap(qwq[2] ,qwq[3]);
for(int i = 1 ; i <= n ; ++i){
if(find(i) != lead[qwq[1]]) continue;
for(int j = 1 ; j <= n ; ++j){
if(find(j) != lead[qwq[2]]) continue;
if(p[i].mxd(p[j]) <= len){
tag[lshx[p[i].x]][lshy[p[j].y]] = tc;
tag[lshx[p[j].x]][lshy[p[i].y]] = tc;
}
}
}
for(int i = 1 ; i <= n ; ++i){
if(find(i) != lead[qwq[3]]) continue;
for(int j = 1 ; j <= n ; ++j){
if(find(j) != lead[qwq[4]]) continue;
if(p[i].mxd(p[j]) <= len &&
(tag[lshx[p[i].x]][lshy[p[j].y]] == tc
|| tag[lshx[p[j].x]][lshy[p[i].y]] == tc))
return 1;
}
}
}
return false;
}
return false;
}
int main(){
cin >> n;
for(int i = 1 ; i <= n ; ++i){
cin >> p[i].x >> p[i].y;
X[i] = p[i].x ,Y[i] = p[i].y;
lshx[X[i]] = i;
lshy[Y[i]] = i;
}
sort(X + 1 ,X + 1 + n);
sort(Y + 1 ,Y + 1 + n);
LL l = 0 ,r = 2e9 + 1 ,mid;
while(l <= r){
mid = (l + r) >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
// cerr << l << " " << r << endl;
}
cout << ((r >= 2e9) ? -1 : (r + 1)) << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号