软工个人项目
2020-03-10 00:54 木杉月 阅读(235) 评论(2) 收藏 举报| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目 |
| 教学班级 | 005 |
| 项目的GitHub地址 | IntersectProject |
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 8 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 40 | 60 |
| · Design Spec | · 生成设计文档 | 20 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 30 | 40 |
| · Coding | · 具体编码 | 90 | 100 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 80 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 50 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 388 | 455 |
总的来说这次个人项目并不是很难(也有可能是因为我暴力求解,没有想到优化解的原因),但关键我认为是在于熟悉项目开发流程。特别是测试,还有性能的优化。在之前课程上所写的程序,都是完成基本的输入输出即可,而且对于性能的要求并没有很高。而且一般来说是没有计划的,直接就上手编程,而这次,先设计,再进行编程,明显编程速度快了许多,而且没有存在那种需要大改结构的地方。
解题思路描述
-
首先我看到题目与两直线交点有关,就想有什么好的算法可以求两直线交点呢?而且这次是给的直线上两点来代表一条直线。所以怎么才能够用两条直线的两点来求两条直线的交点呢。带着这个问题我就去搜索了,最好得出答案,有以下公式。已知直线l1两点(x0,y0),(x1,y1),直线l2两点(x2,y2),(x3,y3)。
a = y1-y0, b = x1y0-x0 * y1, c = x1-x0, d = y3-y2, e = x3 * y2-x2 * y3, f = x3-x2
y = float(ae-bd)/(af-cd)
x = float(yc-b)/a -
这样我就得到了基础思路,直接通过上面的公式,算出每两条直线的交点,将其中重复的去掉。
-
而如何保存两条直线的交点呢,由于需要去重,所以我选择了hashmap,这样的话,可以以O(1)的时间复杂度寻找某一个点,寻找是否有重复的时候也比较简单。(这里后期进行性能优化时将hashmap替换成了set容器)
-
得到了最基础的解题思路后,我就在想,还有什么性能更好的方法吗?算两直线的交点,是否用其他的方法算会更优,而且一定需要算出直线的交点吗?而我带着这个疑惑去网上搜寻答案,也和同学之间进行了相互的讨论,但是自己还是没有找到一种可以不用算出直线的交点方法。
-
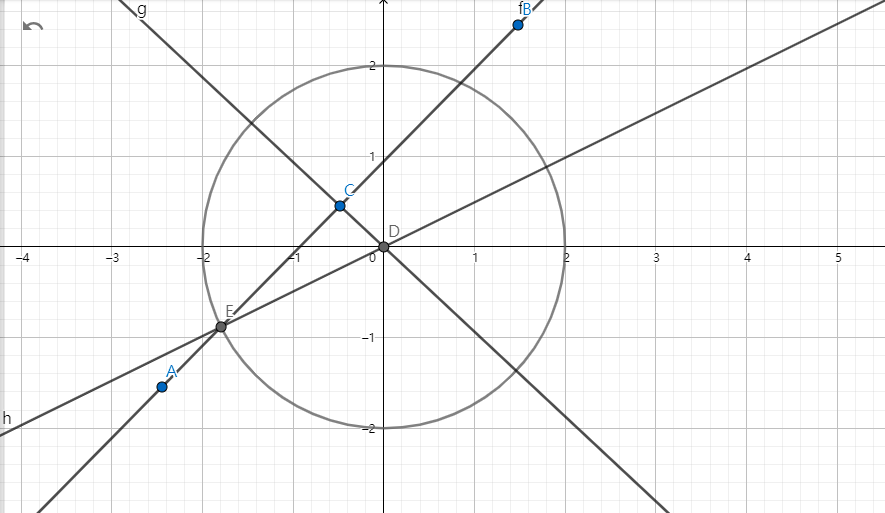
然后再是附加题。附加题中加入了圆这个几何图形,所以题目从直线与直线交点变成了直线与直线交点,直线与圆的交点,圆与圆的交点。而圆与圆的交点可以转化为圆与直线的交点,所以只用解决直线与圆的交点了。而由于解二元一次方程并不现实,所以我就采取了几何的思路去求解。算出点到点的距离,根据向量知识求解其他的点。
![]()
如图所示,已知直线AB与圆R,我们可以算出C点坐标也就是垂足,然后又可以算出CD的长度,而ED就是圆的半径所以EC的长度可以通过勾股定理求得。然后根据直线AB的斜率和C点坐标求得E点坐标即可。
设计实现过程
- 由于这次项目几何图像较少,所以我采用了结构体来存储直线和圆,其中直线存储直线方程的一般式,ax+b = cy圆存储圆心和半径。
-
然后这次设计可以分为以下几步
- 从文件读入数据,分别将直线和圆存入不同容器中
- 遍历直线容器,计算直线与直线的距离(一个函数)
- 遍历直线与圆容器,计算直线与圆的距离(一个函数)
- 遍历圆与圆容器,计算圆与圆的距离(一个函数)
- 输出结果
-
这三个函数之间,从上到下,下面的函数会使用上面的函数来计算结果。
-
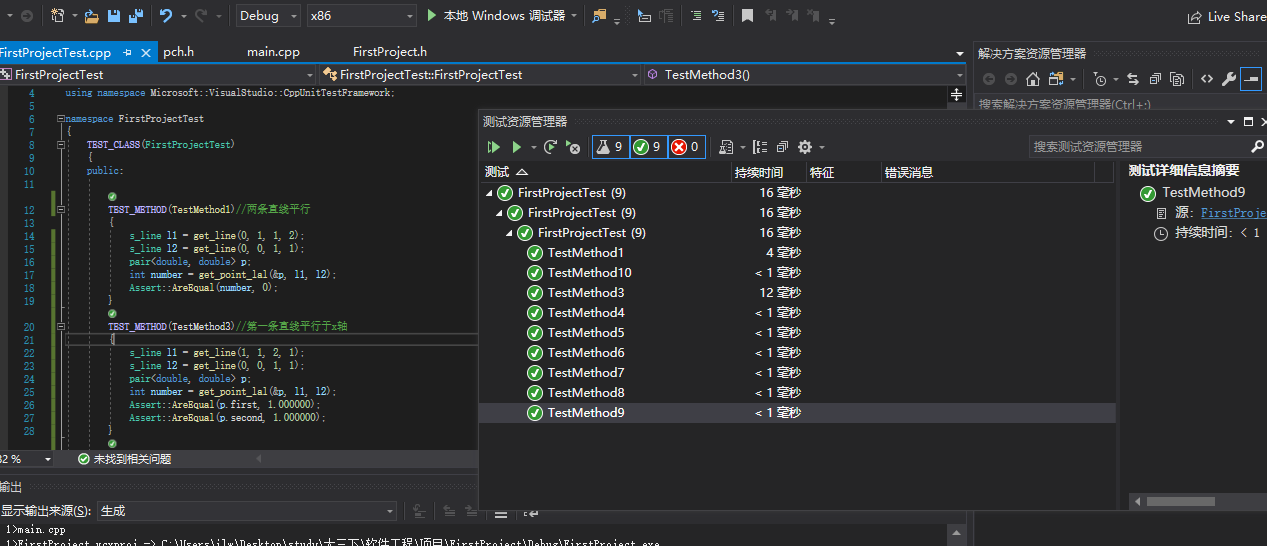
单元测试
-
在这次测试中,分别对应三个函数,根据其几何特性来写测试数据。
![]()
其中直线有相交、平行、直线平行于x轴、直线平行于y轴等等特殊情况。
直线与圆有相交、相切相离这三种情况。
圆与圆有相交、内切、外切、相离这四种情况。
然后我对于这些特殊的情况都分别给出相应的测试数据来进行测试。
-
性能优化
-
在这次优化时基本上有60分钟左右。而其中有一次较大的改动。在拿到题进行思考的时候,我就想用hashmap来存点,因为会对点进行查询。而key用点的坐标转string来表示。而当我用visual studio来分析时却发现其却占了大部分的时间。主要有double转string这个函数。所以我最后改为了用set容器存取pair<double, double>类型的数据,而这一次也显著提高了性能。
-
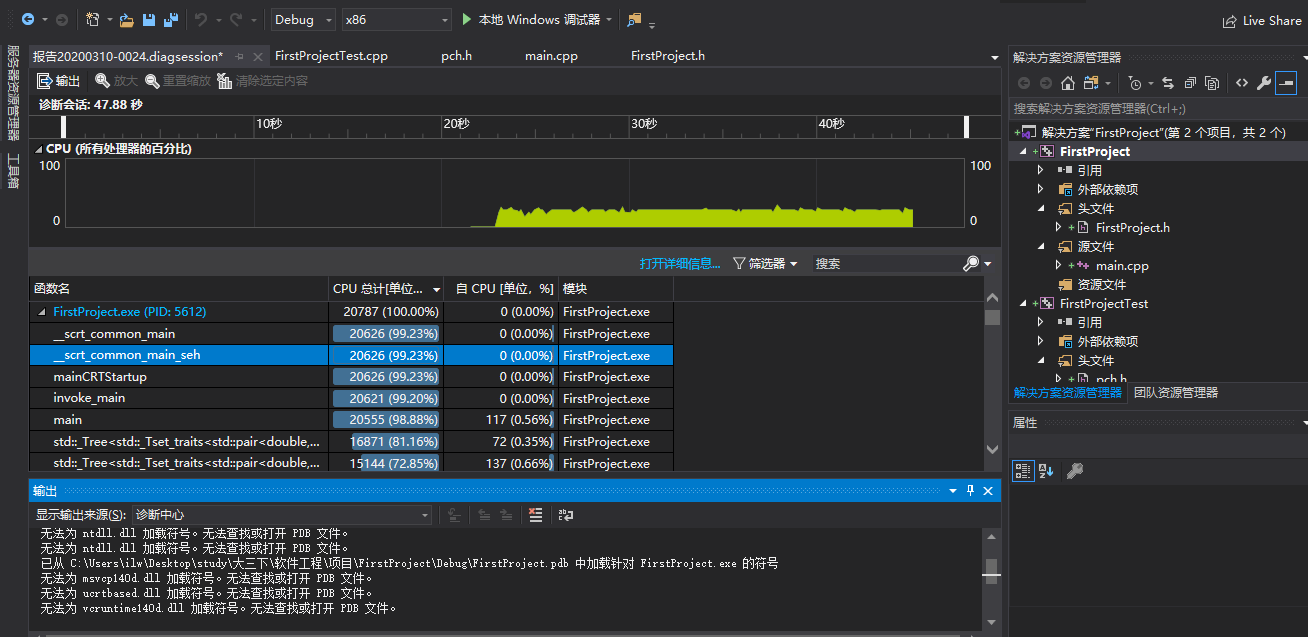
这是这次的性能分析图
![]()
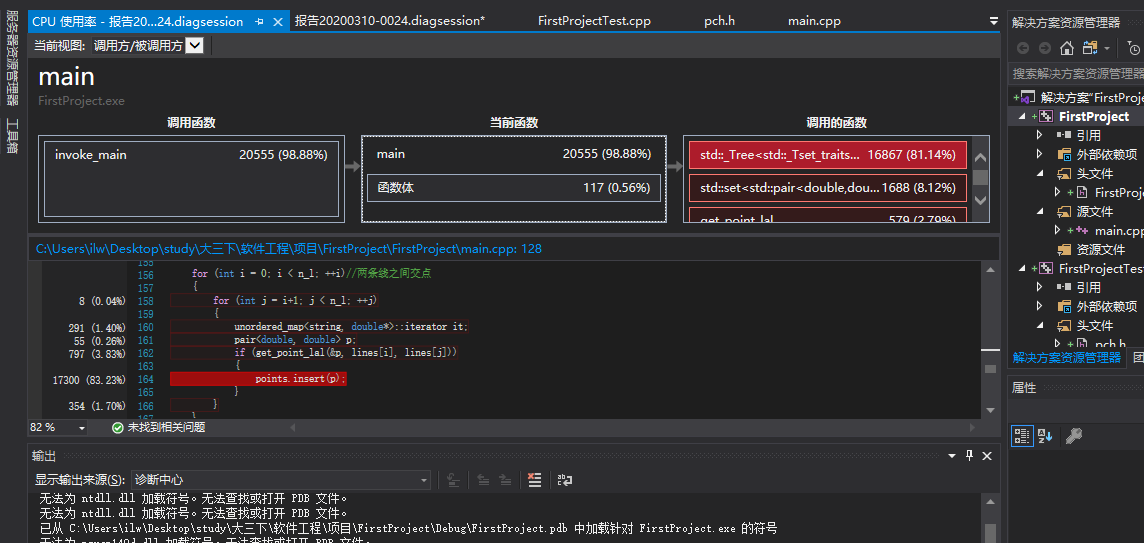
我发现,在计算交点的开销其实还并不是大头,而最重要的消耗其实就是在set的插入上。而开始我用hashmap尽管插入的消耗减小了,但是计算key值却显得消耗更大了。如图所示
![]()
代码说明
-
直线与直线交点
int get_point_lal(pair<double, double>*p, s_line l1, s_line l2) { double a[2]; double y_denominator; y_denominator = (l1.a * l2.c - l1.c * l2.a); if (y_denominator != 0) { if (l1.a == 0) { a[1] = (double)l1.y; a[0] = (l1.y * l2.c - l2.b) / l2.a; } else { double x = (l1.a * l2.b - l1.b * l2.a) / (y_denominator); a[1] = x; a[0] = (x * l1.c - l1.b) / l1.a; } *p = make_pair(a[0], a[1]); return 1; } return 0; }返回交点个数,变量p存储交点。传入两条直线的结构体。而具体计算过程就是简单的几何知识,就可以然后用代码翻译一下就行了。
-
直线与圆的交点
int get_point_lac(pair<double,double> *p,s_line l, s_circular c) { double length = distance(c, l); if (c.r < length) { return 0; } s_line new_l; new_l.a = -l.c; new_l.c = l.a; new_l.b = -new_l.a * c.x + new_l.c * c.y; new_l.x = (int)c.x; new_l.y = (int)c.y; pair<double, double> s; int m; m = get_point_lal(&s, l, new_l); if (c.r == length) { p[0] = s; return 1; } double t = sqrt((double)c.r * c.r - length * length); double sq = sqrt(l.a * l.a + l.c * l.c); double x_add = t * l.c / sq; double y_add = t * l.a / sq; p[0] = make_pair(s.first+x_add, s.second+y_add); p[1] = make_pair(s.first-x_add, s.second-y_add); return 2; }返回值也是交点的个数。而具体的计算过程,也在上面的解题思路上所描写。同样p也是存储的交点坐标。
-
圆与圆的交点
int get_point_cac(pair<double, double> *p, s_circular c1, s_circular c2) { double length = sqrt((c2.y - c1.y) * (c2.y - c1.y) + (c2.x - c1.x) * (c2.x - c1.x)); if (length > c1.r + c2.r || length < abs(c1.r - c2.r)) { return 0; } double length_e = (c1.r * c1.r - c2.r * c2.r + length * length) / (2 * length); double a = c2.y - c1.y; double c = c2.x - c1.x; double sq = sqrt(a * a + c * c); double x_e = c1.x + length_e * c / sq; double y_e = c1.y + length_e * a / sq; if (length == c1.r + c2.r || length == abs(c1.r-c2.r)) { *p = make_pair(x_e, y_e); return 1; } double length_new = sqrt(c1.r * c1.r - length_e * length_e); double temp = a; a = -c; c = temp; p[0] = make_pair(x_e + length_new * c / sq, y_e + length_new * a / sq); p[1] = make_pair(x_e - length_new * c / sq, y_e - length_new * a / sq); return 2; }与第二个函数类似,也是算出交线的中点,再根据勾股定理计算交点。而参数设置也是p存储交点坐标。返回值也是交点个数。
Code Quality Analysis
结语
这一次也是自己从头到尾完完整整利用工具来完成一个项目,之前debug,性能分析的时候,自己经常是肉眼观察,或者是printf输出。而这一次利用VS219来完成这个项目,让我感受到了VS2019的魅力,尽管刚开始上手时会有点畏惧,但是当自己完整的使用了一遍,发现其实是很容易上手的,而且功能十分完整,且清晰明了。测试可以根据具体的单个函数进行测试,性能分析有图形界面。这也是为后面的结对编程和团队项目准备吧。总的来说,这一次个人项目,虽然题目不难,但是收获却很大。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号