题解 CF383C 【Propagating tree】
这道题明明没有省选难度啊,为什么就成紫题了QAQ
另:在CF上A了但是洛谷Remote Judge玄学爆零。
思路是DFS序+线段树。
首先这道题直观上可以对于每一次修改用DFS暴力O(n),然后对于询问O(1)解决。
但是这个方法实在是太耗时间了,因此我们想到了dfs序。
所谓dfs序,就是按照dfs(这里我们用先序遍历)的顺序给这颗树打上一个标签。
然后我们就可以把这颗树“拍平”,用一些支持区间修改单点查询的数据结构log级别解决问题了。
当然这样粗略地说一遍肯定会有人看不懂,还是通过一个实例讲解好一点。
举个例子,我们有这样一棵树:
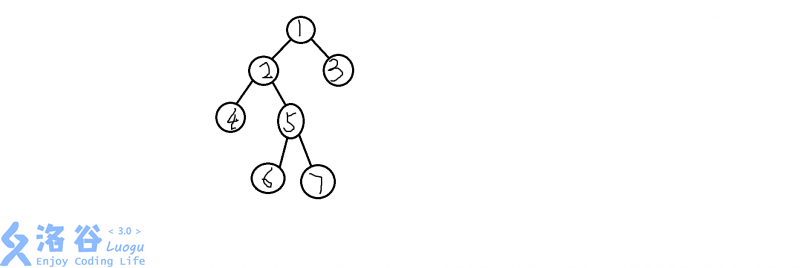
每个节点都有一个编号。现在,我们按照dfs的顺序将这颗树写出来,也就是:
1 1 2 4 5 6 7 3
这样这颗树已经被我们“拍平”了,但是仍然无法解题。
为什么?
因为对于每一颗子树,你只知道它从什么地方开始,不知道它在什么地方结束。
解决方案很简单,我们多记录一个out,表示回溯的时候的顺序,这样就可以解决问题了。
dfs这个部分的代码如下:
1 void dfs(int x){ 2 in[x]=++dfn; //in是子树的起点。 3 for(int i=head[x];i;i=edge[i].next){ 4 int y=edge[i].to; 5 if(father[x]==y)continue;//father数组储存节点的父亲。(废话) 6 dep[y]=dep[x]+1,father[y]=x,dfs(y);//dep数组储存节点的深度,这个数组的必要性我们后面会提到。 7 } 8 out[x]=dfn; //out是子树的中点。 9 }
然后现在考虑怎么做这道题。
很显然,最大的难点在于每次更新对于每一层节点改变的值都不一样。
等等,每一层?
对的,可以发现,相邻层的节点变化值互为相反数,而相隔层的节点变化值相同。
如果想不出解决方案这道题巨难,但如果想出来了就是一道水题。
很简单,线段树维护节点的变化值,然后在更新时我们对于层数为奇数的节点加上变化值,对于层数为偶数的节点减去变化值。
这样层数为奇数的节点与层数为偶数的节点变化量肯定是反的,也就符合题意。
实现是这样的:
1 scanf("%d%d",&op,&x); 2 if(op==1)scanf("%d",&y),add(1,in[x],out[x],dep[x]%2?y:-y); 3 else printf("%d\n",a[x]+query(1,x)*(dep[x]%2?1:-1));
这个玩意的正确性很好说明,自己模拟一下就OK了。
------------
总的来说,这道题就是敲个模板。
代码如下:
1 #include<iostream> 2 #include<cstdio> 3 #define ls p<<1 4 #define rs p<<1|1 5 using namespace std; 6 const int N=2000200; 7 int n,m,v,u,cnt,op,x,dfn,y; 8 int a[N],in[N],head[N],dep[N],out[N],father[N]; 9 struct node{int to,next;}edge[N]; 10 inline void add(int a,int b){edge[++cnt].to=b,edge[cnt].next=head[a],head[a]=cnt;} 11 struct tnode{int add,sum,l,r;}tree[N<<2]; 12 void dfs(int x){ 13 in[x]=++dfn; 14 for(int i=head[x];i;i=edge[i].next){ 15 int y=edge[i].to; 16 if(father[x]==y)continue; 17 dep[y]=dep[x]+1,father[y]=x,dfs(y); 18 } 19 out[x]=dfn; 20 } 21 inline void pushup(int p){ 22 tree[p].sum=tree[ls].sum+tree[rs].sum; 23 } 24 inline void pushdown(int p,int l,int r){ 25 if(!tree[p].add)return; 26 int mid=(l+r)>>1; 27 tree[ls].add+=tree[p].add;tree[rs].add+=tree[p].add; 28 tree[ls].sum+=tree[p].add*(mid-l+1);tree[rs].sum+=tree[p].add*(r-mid); 29 tree[p].add=0; 30 } 31 void build(int p,int l,int r){ 32 tree[p].l=l,tree[p].r=r; 33 tree[p].add=tree[p].sum=0; 34 if(l==r)return; 35 int mid=(l+r)>>1; 36 build(ls,l,mid);build(rs,mid+1,r); 37 pushup(p); 38 } 39 void add(int p,int l,int r,int val){ 40 if(l<=tree[p].l&&tree[p].r<=r){tree[p].add+=val;tree[p].sum+=(tree[p].r-tree[p].l+1)*val;return;} 41 int mid=(tree[p].l+tree[p].r)>>1; 42 pushdown(p,tree[p].l,tree[p].r); 43 if(l<=mid)add(ls,l,r,val); 44 if(r>mid)add(rs,l,r,val); 45 pushup(p); 46 } 47 int query(int p,int x){ 48 if(tree[p].l==tree[p].r)return tree[p].sum; 49 int mid=(tree[p].l+tree[p].r)>>1; 50 pushdown(p,tree[p].l,tree[p].r); 51 if(x<=mid)return query(ls,x); 52 else return query(rs,x); 53 } 54 int main(){ 55 scanf("%d%d",&n,&m); 56 for(int i=1;i<=n;++i)scanf("%d",&a[i]); 57 for(int i=1;i<=n-1;++i){ 58 scanf("%d%d",&v,&u); 59 add(v,u); 60 } 61 dfs(1); 62 build(1,1,n); 63 while(m--){ 64 scanf("%d%d",&op,&x); 65 if(op==1)scanf("%d",&y),add(1,in[x],out[x],dep[x]%2?y:-y); 66 else printf("%d\n",a[x]+query(1,x)*(dep[x]%2?1:-1)); 67 } 68 return 0; 69 }

