凸包
简介
(本文只讨论二维凸包)
粗略地看,凸包是对凸多边形的另一种称呼。
更加准确地说,对于二维平面上给定的点集,其凸包为包含了点集且由点集中的点连接而成的凸多边形。
在解题时,一般询问与凸包周长或面积相关的极值问题。
前置知识
向量
如果实在没有接触过向量的概念,那么大致将其想象为一个箭头就行了。
我们一般用坐标\((x,y)\)表示向量,意为从原点指向\((x,y)\)的箭头。
向量运算
向量的加法和减法结果均为向量:
\((x_1,y_1)±(x_2,y_2)=(x_1±x_2,y_1±y_2)\)
向量的乘法分为两种,点乘和叉乘,结果均为实数:
点乘表示向量\(a\)在向量\(b\)上的投影长度,\((x_1,y_1)*(x_2,y_2)=x_1y_1+x_2y_2\)
叉乘表示向量\(a\)和向量\(b\)共起点时组成的平行四边形面积,\((x_1,y_1)\land(x_2,y_2)=x_1y_2-x_2y_1\)
向量没有除法。
实现思路
实现采用的是\(Graham\)扫描法。
我们选定点集中的一个点为原点,然后将根据所有点与其连线的斜率从大到小排序。
一般我们倾向于选择左下角的点,但是点的选择几乎不造成影响。
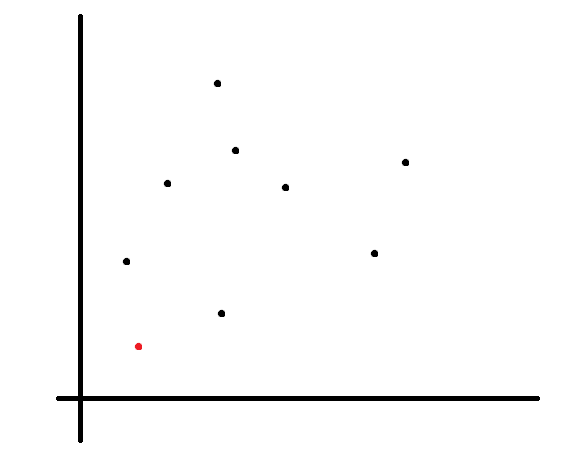
显然斜率最小的点在凸包的边上。
对于剩下的所有点,枚举此前所有的点,考虑加入后是否会出现内凹。如果出现内凹,显然此前存在非最优的选点。
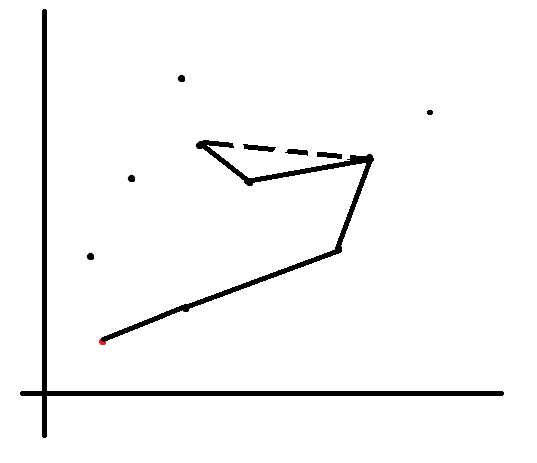
对于上图中的情况,选择虚线是更优的解。
我们可以通过维护一个单调栈来实现这个过程。
在上面的判断中,判断是否出现内凹有多种思路,其中通过叉乘判断是较快的。
若叉乘为负数,则内凹,反之外凸,结论显然。

