P4264 [USACO18FEB] Teleportation S 题解

• 博客阅读体验更佳
• 题目传送门

题意

• 有 \(n\) 个物品，分别需要从 \(a_i\) 运输到 \(b_i\) 处，\(x=0\) 处有一个传送门入口，选择一个传送门出口 \(y\)，使得总运输距离 \(d\) 最小，输出最小值。

分析

• 很明显，传送门对于总距离 \(d\) 的贡献是可以拆分成对于每一个物品的贡献之和的，因为有 \(d=\sum d_i\)。
• 然后我们分析一下 \(y\) 的选址对于每一个物品的 \(d_i\) 的贡献。
• 通过画图和分类讨论可以发现，一共有两种情况，而且每个 \(y\) 对应的 \(d_i=f_i(y)=\min(|a_i-b_i|,|a_i|+|b_i-y|)\) 是分段且线性的，根据线性函数的一些性质，我们可以利用对斜率的差分来求解 \(d=\min_{y\in \mathbb{R}}{\sum f_i(y)}\)。

画图

1. \(|a|>|a-b|\)

• 这时候肯定不会走传送门的，因为运去 \(x=0\) 那里都比直接运要远。

2. \(|a|<|b|\)
   
   

• 如图所示，这种情况下三个分段点分别是 \(2a\)，\(b\) 和 \(2b-2a\)。

3. \(a<0<b/b<0<a\)
   
   

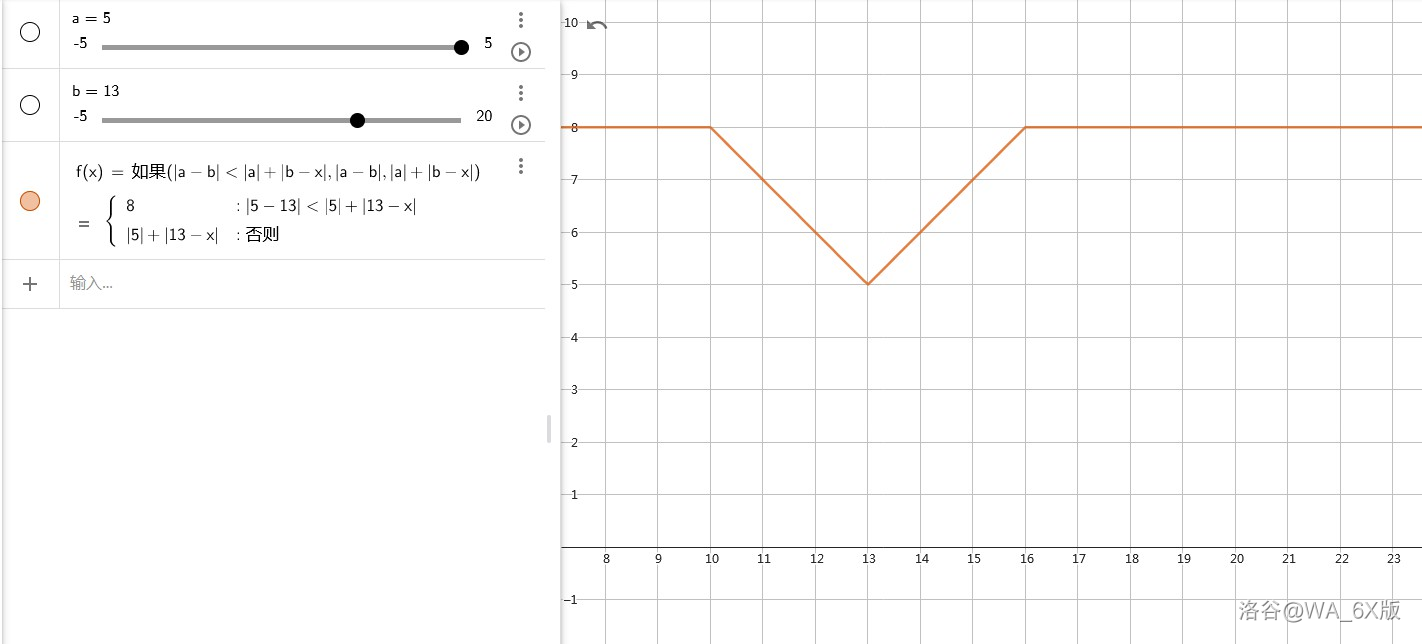
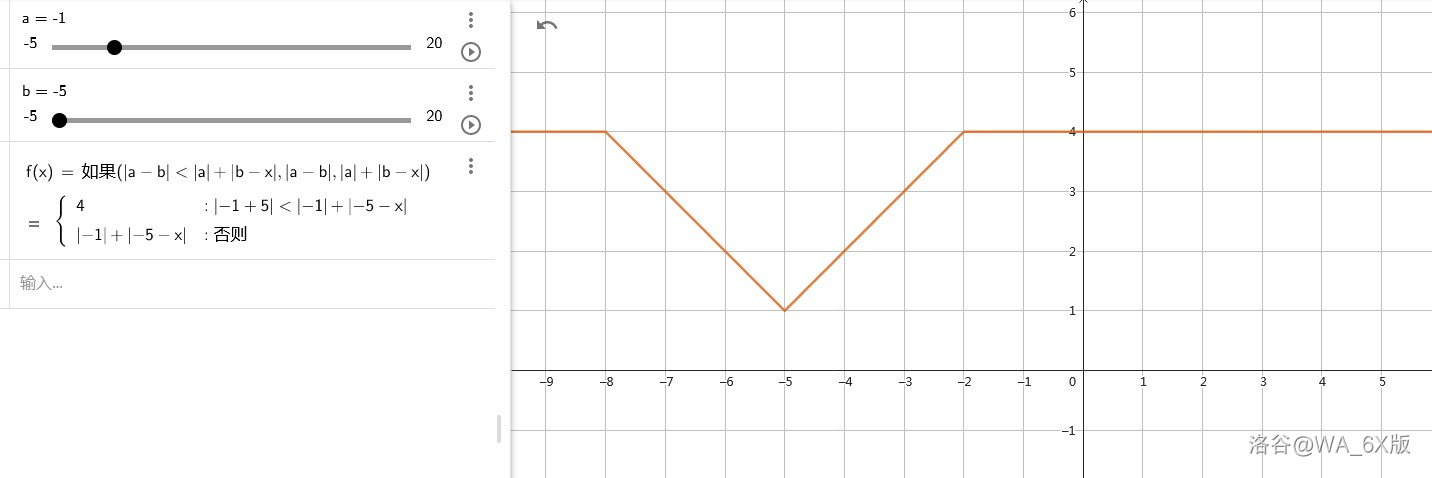
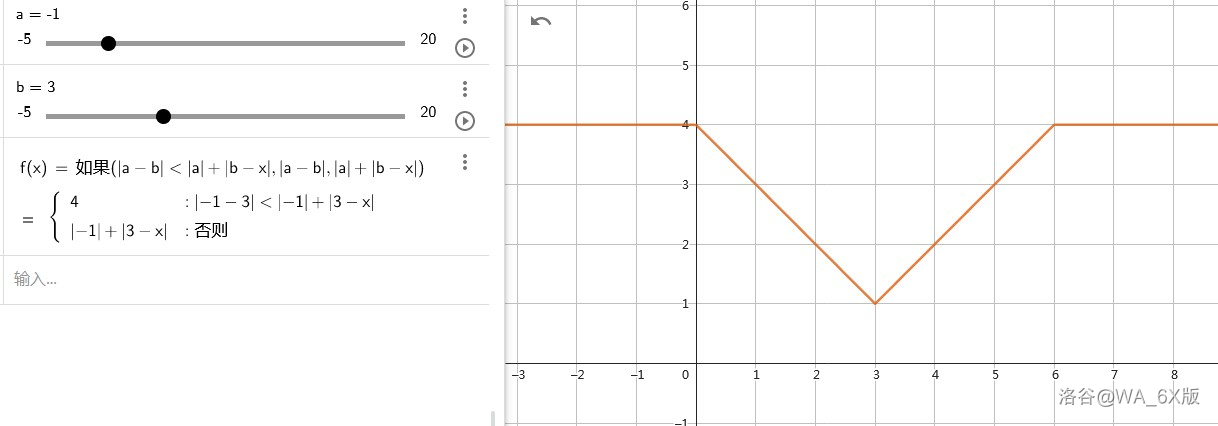
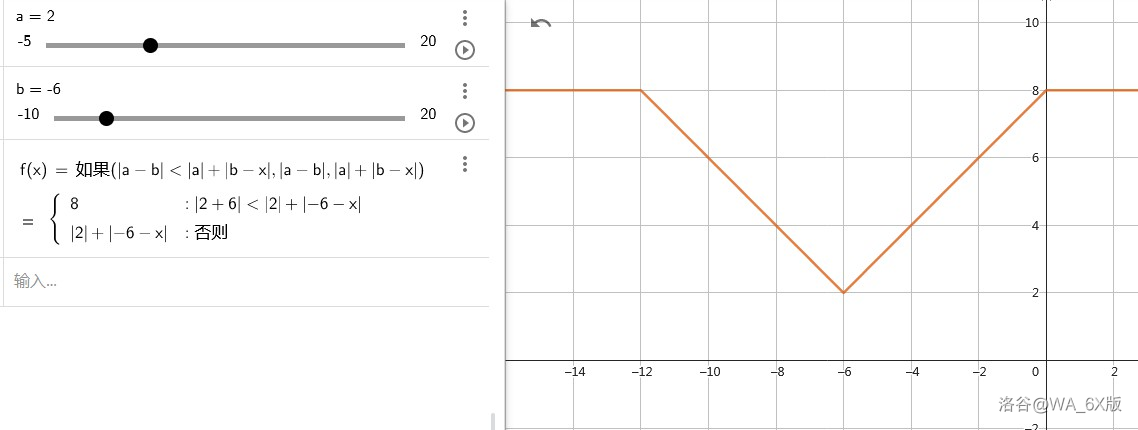
• 如图所示，这种情况下的三个分段点是 \(0\)，\(b\) 和 \(2b\)。
• 而且，这三种情况的初始值均为 \(|a-b|\)，所以初始值 \(f(-\infty)\) 要设成 \(\sum|a_i-b_i|\)。

实现

• 对于每一个物品，根据上图分类后利用 map 来存储差分的数组。对第一个分段位置 \(-1\)，对第二个 \(+2\)，最后一个 \(-1\)。处理完之后按 \(y\) 的值从小到大遍历 map，对于每一个 \(f(y)\) 的分段点的值求最小值即可。

代码

#include <bits/stdc++.h>
#define inf 0x7fffffff
#define int long long
using namespace std;
int n, x, y = -inf, s, ans;
map<int, int> mp;

inline void read(int &x) {
	int w = 1;
	char ch = x = 0;
    while (ch < '0' || ch > '9') {
    	if (ch == '-') w *= -1;
    	ch = getchar();
	}
    while(ch >= '0' && ch <= '9') {
    	x = (x << 1) + (x << 3) + ch - 48;
		ch = getchar();
	}
	x *= w;
	return ;
}

signed main() {
	read(n);
	int a, b;
	for (int i = 1; i <= n; i++) {
		read(a), read(b);
		x += abs(a - b);
		if (abs(a) > abs(a-b)) continue; //第一种情况
		mp[b] += 2;
		if ((a < b && a < 0) || (a >= b && a >= 0)) { //处理后两种情况
			mp[0]--;
			mp[b << 1]--;
		} else if ((a < b && a >= 0) || (a >= b && a < 0)) {
			mp[(b - a) << 1]--;
			mp[a << 1]--;
		}
	}
	ans = x;
    int now, tmp;
	for (auto it : mp) { //对于每一个分段点都统计，取最小值
		now = it.first, tmp = it.second;
		x += s * (now - y);
		y = now;
		s += tmp;
		ans = min(ans, x);
	}
	printf("%lld", ans);
	return 0;
}