Slope trick 学习笔记

博客传送门

Slope trick 的定义

Slope trick 是一种通过分析 DP 函数在转移时的斜率变化来优化转移的技巧。通常来说，被维护的函数图像是离散的凸函数，Slope trick 会维护函数的斜率或者斜率的差分。

维护凸函数主要有以下几个优点：

1. 方便维护形如 \(dp'[i]\leftarrow \max(dp[i],dp[i-1]+x)\) 的操作（等会的例题会讲怎么维护）。

2. 方便维护加法操作，两个凸函数相加仍然是凸函数。

3. 方便维护 \(\max\) 加法卷积操作（形如 \(h_k=\max_{i+j=k}(f_i+g_j)\)）。

4. 维护差分后方便快速找极值。

题目引入

Buy Low Sell High

这道经典题有多种做法和理解方式，这里仅介绍从 Slope trick 角度出发的思路。

首先令 \(dp[i][j]\) 表示第 \(i\) 天结束时持有 \(j\) 份股票的最大的收益。方便起见，我们可以强制在每天开始时买一份，然后决策就变成了卖 \(0\sim 2\) 份。不妨令 \(f[j]\) 表示当前的 DP 图像，\(f'[j]\) 表示变化后的图像，那么第 \(i\) 天时 DP 图像的变化为：

• （\(1\)）\(f'[j]\leftarrow f[j-1]-p_i\)（买一份）
• （\(2\)）\(f'[j]\leftarrow \max(f[j],f[j+1]+p_i)\)
• （\(3\)）\(f'[j]\leftarrow \max(f[j],f[j+1]+p_i)\)

可以发现 \(f\) 的图像始终是凸的。

感性认知一下：\(f_i[j]\) 表示第 \(i\) 天手上有 \(j\) 份股票。因为每天只能卖一份，所以每天肯定先卖最贵的一份，所以卖的越多新卖的那个就越不值钱。\(f_i[j]-f_i[j+1]\) 表示多卖的一张股票的价格，那么 \(f_i[j]-f_i[j+1]\) 是递减的，因此 \(f\) 的图像应该是凸的。

证明：（a）构建费用流模型；（b）归纳法（\(\max\) 加法卷积）。下面用归纳法证明。

假设 \(f\) 是凸函数，我们需要证明经过上面的 \(123\) 三个操作后 \(f'\) 也是凸函数。

首先，第 \(1\) 个操作就相当于把 \(f\) 向右平移一格然后向下平移 \(p_i\) 格，因此函数图像凹凸性不变。然后看 \(23\) 操作，假设有 \(g\) 函数，满足 \(g(0)=0\)，\(g(-1)=p_i\)，那么 \(f'\) 就等于 \(f\) 和 \(g\) 进行 \(\max\) 加法卷积操作的结果。因为 \(g\) 就只有两个值，所以可以认为 \(g\) 是一个凸函数，因为两个凸函数进行 \(\max\) 加法卷积的结果还是凸函数（这个可以用闵可夫斯基和证，这里就不证了），所以 \(f'\) 是凸函数。因此 \(f\) 的图像始终是凸的。

我们把 \(f\) 变化前后的图像画出来：

\(f\) 的图像是凸函数有什么用呢？观察 \(23\) 操作，其本质上就是：如果 \(f[k+1]+p_i\le f[k]\)，那么不转移；如果 \(f[k+1]+p_i>f[k]\)，则进行转移。注意到 \(f\) 是凸的，因此只有左边会进行转移，而右边不会。则左边就是一段原本的函数图像向左平移一格，然后向上平移 \(p_i\) 格（如上图中黑色线段的 \([0,3]\) 的部分就是红色线段 \([1,4]\) 部分平移的结果）。

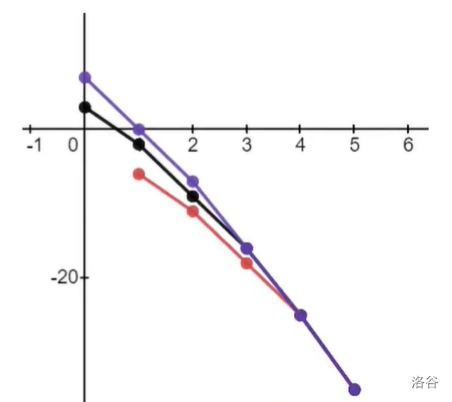
根据上面的理论，对于左边进行了转移的那一部分，我们有 \(f'[k-1]-f'[k]=f[k]-f[k+1]\)，因此新的 \(f'\) 在 \(i\) 位置上的差分就等于 \(f\) 在 \(i+1\) 位置上的差分。因此第 \(i\) 天的操作就是删除最小的（也就是最左端的）斜率，然后再插入一个斜率 \(p_i\)。

我们用堆来维护斜率，最终答案就是最左上角的高度。因为右下角的高度是 \(\sum_{i=1}^n-p_i\)（每天第 \(1\) 个操作要向下平移），而高度差可以在每次进行操作 \(23\) 时统计。代码如下，非常简单，复杂度 \(O(n\log n)\)。

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, ans;
priority_queue<int, vector<int>, greater<int>> que;

inline int read(int &x) {
	char ch = x = 0;
	int m = 1;
	while (ch < '0' || ch > '9') {
		ch = getchar();
		if (ch == '-') m *= -1;
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + ch - 48;
		ch = getchar();
	}
	x *= m;
	return x;
}

signed main() {
	read(n);
	int p;
	for (int i = 1; i <= n; i++) {
		read(p);
		if (!que.empty() && que.top() < p) {
			ans += p - que.top();
			que.pop();
			que.push(p);
		}
		que.push(p);
	}
	printf("%lld", ans);
	return 0;
}

总结一下：当我们确定 DP 图像是凸的时，我们可以利用凸函数的性质（如：斜率单调，找极值等）快速维护状态转移对应的图像变化。再知道图像其中一个位置的值后，就可以通过斜率把所有 DP 值恢复过来。这一类题目往往要先发现凸性，然后要通过画图来感受转移带来的图像变化，选择合适的维护方式。

P3642 [APIO2016] 烟火表演

题目传送门

同上处理，令 \(f_i[x]\) 表示 \(x\) 秒引爆第 \(i\) 个节点的子树的代价，\(l\) 为 \(i\) 与 \(fa[i]\) 的距离。可以发现，\(f\) 应该是一个向下凸的函数。令\(f\) 为原函数，即 \(f_i\)；\(f'\) 为新函数，即 \(f_{fa[i]}\)，且 \(f\) 在区间 \([L,R]\) 上取到最小值。推 dp 式子可以知道，\(f\) 对 \(f'[x]\) 的贡献应该是 \(F[x]=\min_{k\le x}\{f[k]+|l-x+k|\}\)。然后我们对 \(x\) 分讨。

• （\(1\)）当 \(x<L\) 时，这时直接修改 \(l\) 肯定比修改下面子树更优，从式子上看就是 \(k\) 越大越好，所以直接让 \(k=x\)，得到 \(F[x]=f[x]+l\)。

• （\(2\)）当 \(x>R+l\) 时，从式子知道，因为 \(f[k]\) 在 \(k\ge R\) 时的变化率不小于 \(k\) 的变化率，所以 \(k\) 越接近 \(R\) 越好，因此让 \(k=R\)，得到 \(F[x]=f[R]-l+x-R\)。

• （\(3\)）当 \(L\le x<L+l\) 时，因为 \(k\in(L,L+l)\) 时 \(F[x]\) 在上升，\(k\le L\) 时 \(f[k]\) 比 \(k\) 变化的更快，因此 \(F[x]\) 在下降，所以我们让 \(k=L\)，于是有 \(F[x]=f[L]+l-x+L\)。

• （\(4\)）当 \(L+1\le x\le R+l\) 时，令 \(k=x-l\) 时明显是最小的，此时 \(F[x]=f[L]\)。

看一看这些操作在斜率数组上是怎样的（这里一定要画一下图！这样会更容易理解！）：操作 \(1\) 是将 \(f\) 向上平移 \(l\) 格；操作 \(2\) 是将 \(f\) 的斜率修改为 \(1\)；操作 \(3\) 是将斜率改为 \(-1\)；操作 \(4\) 是将 \(f\) 向右平移 \(l\) 格。

因为要实现函数的加法，直接维护斜率不好维护，所以这里我们维护斜率的拐点（或者说差分），让一个拐点表示斜率在这个位置加一（所以拐点可重）。令 \(i\) 有 \(w\) 个儿子，因为合并一个儿子会增加一个斜率为正的拐点，因此删除 \(w-1\) 个最大的拐点，接下来两个是 \(R\) 和 \(L\)，也删除之后加入 \(L+l\) 和 \(R+l\) 就得到了 \(F\) 的拐点表示堆，然后把 \(F\) 的拐点合并进 \(f'\)。我们已知 \(f_1[0]=\sum_{i=1}^nl_i\)，答案就是 \(f_1\) 的最小值。这些操作可以用可并堆完成，时间复杂度 \(O((n+m)\log(n+m))\)，代码如下。

#include <bits/stdc++.h>
#define int long long
#define N 600005
using namespace std;
int n, m, fa[N], l[N], num[N], rt[N], ans, tot;

struct node {
	int l, r, val, dis;
} t[N];

inline int read(int &x) {
	char ch = x = 0;
	int m = 1;
	while (ch < '0' || ch > '9') {
		ch = getchar();
		if (ch == '-') m *= -1;
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + ch - 48;
		ch = getchar();
	}
	x *= m;
	return x;
}

int merge(int x, int y) {
	if (!x || !y) return x + y;
	if (t[x].val < t[y].val) swap(x, y);
	t[x].r = merge(t[x].r, y);
	if (t[t[x].l].dis < t[t[x].r].dis) swap(t[x].l, t[x].r);
	t[x].dis = t[t[x].r].dis + 1;
	return x;
}

inline int pop(int x) {
	return merge(t[x].l, t[x].r);
}

signed main() {
	read(n), read(m);
	for (int i = 2; i <= n + m; i++) {
		read(fa[i]), read(l[i]);
		num[fa[i]]++;
		ans += l[i];
	}
	for (int i = n + m; i > 1; i--) {
		int L = 0, R = 0;
		if (i <= n) {
			while (--num[i]) rt[i] = pop(rt[i]);
			R = t[rt[i]].val, rt[i] = pop(rt[i]);
			L = t[rt[i]].val, rt[i] = pop(rt[i]);
		}
		t[++tot].val = L + l[i];
		t[++tot].val = R + l[i];
		rt[i] = merge(rt[i], merge(tot, tot - 1));
		rt[fa[i]] = merge(rt[fa[i]], rt[i]);
	}
	while (num[1]--) rt[1] = pop(rt[1]);
	while (rt[1]) ans -= t[rt[1]].val, rt[1] = pop(rt[1]);
	printf("%lld", ans);
	return 0;
}

感谢围观！如有错误请大佬们指出！